
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные теоремы двойственности
Связь между оптимальными решениями двойственных задач устанавливается с помощью теорем двойственности.
Основное неравенство теории двойственности.Пусть имеется пара двойственных задач I и II. Покажем, что для любых допустимых решений  и
и  прямой и двойственной задач справедливо неравенство
прямой и двойственной задач справедливо неравенство
 или
или  . (7.7)
. (7.7)
Доказательство. Умножив неравенства системы ограничений (7.2) прямой задачи  соответственно на переменные y1, ¼, ym и сложив правые и левые части полученных неравенств, имеем
соответственно на переменные y1, ¼, ym и сложив правые и левые части полученных неравенств, имеем
 . (7.8)
. (7.8)
Аналогично преобразовав систему ограничений (7.5) двойственной задачи  путем умножения обеих частей неравенства на переменные х1, ¼, хn и последующего их сложения, получим
путем умножения обеих частей неравенства на переменные х1, ¼, хn и последующего их сложения, получим
 . (7.9)
. (7.9)
Так как левые и правые части неравенств (7.8) и (7.9) представляют одно и то же выражение  , то в силу свойства транзитивности неравенств получим доказываемое неравенство (7.7).À
, то в силу свойства транзитивности неравенств получим доказываемое неравенство (7.7).À
Теперь можно перейти к признакам оптимальности решений.
Достаточный признак оптимальности. Сформулируем теорему.
Теорема 1. Если  и
и  - допустимые решения взаимодвойственных задач, для которых выполняется равенство
- допустимые решения взаимодвойственных задач, для которых выполняется равенство
 , (7.10)
, (7.10)
то 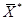 - оптимальное решение прямой задачи I, а
- оптимальное решение прямой задачи I, а  - двойственной задачи II.
- двойственной задачи II.
Доказательство. Пусть  - любое допустимое решение прямой задачи I. Тогда на основании основного неравенства (7.7) получим
- любое допустимое решение прямой задачи I. Тогда на основании основного неравенства (7.7) получим  . Однако
. Однако  - произвольное решение задачи I, отсюда в силу равенства (7.10) следует, что
- произвольное решение задачи I, отсюда в силу равенства (7.10) следует, что  , т.е.
, т.е. 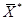 - оптимальное решение прямой задачи I. Аналогично доказывается, что решение оптимально для задачи II.À
- оптимальное решение прямой задачи I. Аналогично доказывается, что решение оптимально для задачи II.À
Кроме достаточного признака оптимальности взаимодвойственных задач существуют и другие важные соотношения между их решениями. Прежде всего возникают вопросы: всегда ли для каждой пары двойственных задач есть одновременно оптимальные решения; возможна ли ситуация, когда одна из двойственных задач имеет решение, а другая нет. Ответ на эти вопросы дает следующая теорема.
Первая (основная) теорема двойственности. Если одна из взаимодвойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны:
 , fmax = gmin. (7.11)
, fmax = gmin. (7.11)
Если линейная функция одной из задач не ограничена, то условия другой задачи противоречивы и она не имеет решения.
Из первой части утверждения теоремы (которую принимаем без доказательства) следует, что условие (7.10) является не только достаточным признаком оптимальности решений (доказанным выше), но и необходимым признаком оптимальности решений взаимодвойственных задач.
Утверждение второй части легко доказывается методом от противного. Предположим, что в прямой задаче линейная функция не ограничена, т.е.  , а условия двойственной задачи не являются противоречивыми, т.е. существует хотя бы одно допустимое решение
, а условия двойственной задачи не являются противоречивыми, т.е. существует хотя бы одно допустимое решение  . Тогда в силу основного неравенства теории двойственности (5.7)
. Тогда в силу основного неравенства теории двойственности (5.7)  , что противоречит условию неограниченности
, что противоречит условию неограниченности  . Следовательно, при
. Следовательно, при  в прямой задаче допустимых решений в двойственной задаче быть не может. À
в прямой задаче допустимых решений в двойственной задаче быть не может. À
Экономический смысл первой (основной) теоремы двойственности. План производства  и набор цен (оценок) ресурсов
и набор цен (оценок) ресурсов  оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от продукции, найденная при «внешних» (известных заранее) ценах с1, с2, ¼, сn, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам y1, ¼, ym. Для всех же других планов
оказываются оптимальными тогда и только тогда, когда прибыль (выручка) от продукции, найденная при «внешних» (известных заранее) ценах с1, с2, ¼, сn, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам y1, ¼, ym. Для всех же других планов  и
и  обеих задач в соответствии с основным неравенством (7.7) теории двойственности прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
обеих задач в соответствии с основным неравенством (7.7) теории двойственности прибыль (выручка) от продукции всегда меньше (или равна) затрат на ресурсы.
Экономический смысл первой теоремы двойственности можно интерпретировать и так: предприятию безразлично, производить ли продукцию по оптимальному плану  и получить максимальную прибыль (выручку) fmax либо продавать ресурсы по оптимальным ценам
и получить максимальную прибыль (выручку) fmax либо продавать ресурсы по оптимальным ценам  и возместить от продажи равные ей минимальные затраты на ресурсы gmin.
и возместить от продажи равные ей минимальные затраты на ресурсы gmin.
Замечание. Утверждение, обратное по отношению ко второй части основной теоремы двойственности, в общем случае неверно, т.е. из того, что условия исходной задачи противоречивы, не следует, что линейная функция двойственной задачи не ограничена.
Тесная связь между двумя взаимодвойственными задачами проявляется не только в равенстве оптимальных значений их линейных функций, о чем утверждалось в первой (основной) теореме двойственности.
При приведении каждой из взаимодвойственных задач к каноническому виду в систему ограничений прямой задачи I (7.2) вводят m неотрицательных переменных xn+1, xn+2, ¼ xn+m, а в систему ограничений двойственной задачи II – n неотрицательных переменных ym+1, ym+2, ¼ ym+n.
Системы ограничений каждой из взаимодвойственных задач примут вид:
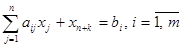 (7.12)
(7.12)
 (7.13)
(7.13)
Установим соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи (табл. 7.2).
Таблица 7.2
| Переменные прямой задачи I | |
| Первоначальные | Дополнительные |

|  (7.14) (7.14)
|
| Дополнительные | Первоначальные |
| Переменные двойственной задачи II |
Теорема 2 (примем без доказательства). Положительным (ненулевым) компонентам оптимального решения одной из взаимодвойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i = 1, 2, ¼, m и j = 1, 2, ¼, n:
если  > 0, то
> 0, то 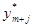 = 0;
= 0;
если  > 0, то
> 0, то  = 0,
= 0,
и аналогично,
если  > 0, то
> 0, то  = 0;
= 0;
если 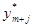 > 0, то
> 0, то  = 0.
= 0.
Из рассмотренной теоремы следует важный вывод о том, что введенное ранее соответствие (7.14) между переменными взаимодвойственных задач при достижении оптимума (т.е. на последнем шаге решения каждой задачи симплексным методом) представляет соответствие между основными (как правило, не равными нулю) переменными одной из двойственных задач и неосновными (равными нулю) переменными другой задачи, когда они образуют допустимые базисные решения.
Рассмотренная теорема является следствием следующей теоремы.
Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции прямой задачи, выраженной через неосновные переменные ее оптимального решения.
Замечание. Если в одной из взаимодвойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденное. Это связано с тем, что при нарушении единственности оптимального решения прямой задачи в выражении линейной функции ее оптимального решения через неосновные переменные отсутствует хотя бы одна из основных переменных.
Третья теорема двойственности. Компоненты оптимального решения двойственной задачи равны значениям частных производных линейной функции fmax(b1, b2, ¼, bm) по соответствующим аргументам, т.е.
 . (7.15)
. (7.15)
Из данной теоремы следует, что объективно обусловленные оценки показывают, насколько денежных единиц изменится максимальная выручка от реализации продукции при изменении запасов соответствующего i-го ресурса на одну единицу.
Дата добавления: 2014-12-03; просмотров: 1172; Мы поможем в написании вашей работы!; Нарушение авторских прав |