Основные кинематические понятия и характеристики.

Механика изучает механическое движение, которое является простейшей формой движения материи. Основная задача механики - определение положения тела в любой момент времени, если известно его начальное положение. В зависимости от методов решения этой задачи механику разделяют на 3 части:

1) статика - учение о механическом равновесии;

2) кинематика - учение о механическом движении без учета причин, вызывающих это движение;

3) динамика – учение о механическом движении с учетом причин, его вызывающих.

Механическое движение - это изменение положения тел или их частей в пространстве с течением времени. Основным объектом изучения в кинематике

является материальная точка. Понятие “материальная точка” есть физическая абстракция, модель, которая вводится для упрощения описания движения.

Материальной точкой называют тело, размерами и формой которого можно пренебречь в условиях данной задачи.

Заменять реальное тело материальной точкой, т.е. объектом, обладающим массой, но не имеющим геометрических размеров, можно только для тех движений, когда справедливо пренебрежение размерами, формой и процессами, происходящими внутри тела. Если реальное тело нельзя заменить материальной точкой, используют другую физическую модель – абсолютно твердое тело.

Абсолютно твердым телом называют тело, деформациями которого можно пренебречь в условиях данной задачи.

В действительности же все реальные тела при воздействии на них деформируются.

Все виды механических движений можно свести к поступательному и вращательному движению. Материальная точка может участвовать только в поступательном движении, прямолинейном или криволинейном, т.к. говорить о вращении точки, не имеющей размеров, бессмысленно.

Поступательным назвали такое движение, при котором любая прямая, проведенная в теле, остается параллельной самой себе (рис.1).

Вращательным назвали такое движение, при котором все точки тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения (рис.2). Ось вращения может находиться вне тела.

Произвольное движение тела можно рассматривать как сочетание поступательного и вращательного движений. Для описания положения и движения тела необходимо выбрать систему отсчета.

Системой отсчета называют связанную с часами систему координат, жестко связанную с некоторым физическим телом, называемым телом отсчета.

Обычно система отсчета представляет собой декартову систему координат, для получения которой в пространстве выбирают тело отсчета О и строят относительно него три взаимно перпендикулярные оси, обычно обозначаемые X,Y,Z.

В такой системе отсчета положение материальной точки М можно задать либо ее координатами М(x,y,z,), либо радиус-вектором . Радиус-вектор однозначно связан с координатами точки и задается следующим образом:

,

где - единичные векторы, направленные вдоль осей координат.

Численное значение вектора определяется соотношением

.

Исходя из симметрии решаемой задачи в качестве системы отсчета могут быть также использованы полярная и косоугольная системы координат.

Для описания движения используют понятия: траектория, путь, перемещение, скорость, ускорение.

Траектория - линия, описываемая точкой в пространстве (прямолинейная или криволинейная).

Если траектория лежит в одной плоскости, движение называют плоским.

DS - длина траектории, [S]=1м.

S – скалярная величина.

Перемещение - вектор, соединяющий начальное и конечное положение точки и направленный к конечному положению; [ ]=1м.

Средняя скорость перемещения равна отношению перемещения к интервалу времени Dt, за которое это перемещение произошло:

Вектор совпадает с вектором перемещения. При Dt®0 уменьшается различие между и DS, вектор перемещения совпадает с касательной к траектории в данной точке.

- мгновенная скорость.

Мгновенная скорость - векторная величина, равная первой производной радиуса-вектора движущейся точки по времени:

При Dt®0 DS®½ ½,

=

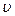Численное значение мгновенной скорости равно первой производной пути по времени.

Примеры скоростей, встречающихся в технике:

пули автомата Калашникова 745м/с

современного боевого самолета 1000м/с

одноступенчатой ракеты несколько тысяч м/с.

Для характеристики быстроты изменения скорости вводится понятие ускорения.

Средним ускорением называют отношение изменения скорости 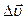к интервалу времени Dt, за которое это изменение произошло.

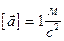
Вектор совпадает с вектором .

- мгновенное ускорение

Мгновенное ускорение - векторная величина, равная первой производной скорости по времени.

Примеры ускорений:

снаряда в стволе при выстреле 70 000 м/с².

ракеты на старте - десятки м/с.

Типы прямолинейного движения.

а) переменное – движение, при котором изменяются как скорость, так и ускорение.

б) равнопеременное движение - движение с постоянным ускорением.

>0 - равноускоренное , < 0 - равнозамедленное

; ;

;

; .

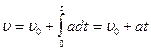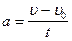в) равномерное движение – движение с постоянной скоростью.

.