
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Угловая скорость и угловое ускорение. Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна j, а направление совпадает с осью
Поворот тела на некоторый угол можно задать в виде отрезка, длина которого равна j, а направление совпадает с осью, вокруг которой производится поворот. Направление поворота и изображающего его отрезка связано правилом правого винта.
В математике показывается, что очень малые повороты можно рассматривать как векторы, обозначаемые символами  или
или  . Направление вектора поворота связывается с направлением вращения тела;
. Направление вектора поворота связывается с направлением вращения тела;  является псевдовектором, так как не имеет точки приложения.
является псевдовектором, так как не имеет точки приложения.
При вращательном движении твердого тела каждая точка движется по окружности, центр которой лежит на общей оси вращения (рис. 7). При этом радиус-вектор R, направленный от оси вращения к точке, поворачивается за время Dt на некоторый угол Dj. Для характеристики вращательного движения вводится угловая скорость и угловое ускорение.
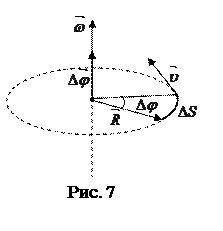 Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени.
Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени.
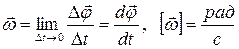 |
 - вектор элементарного поворота тела.
- вектор элементарного поворота тела.
Угол в 1 радиан – это центральный угол, длина дуги которого равна радиусу окружности. 360о = 2p рад.
Направление угловой скорости задается правилом правого винта: вектор угловой скорости сонаправлен с  , то есть с поступательным движением винта, головка которого вращается в направлении движения точки по окружности. Линейная скорость точки связана с угловой скоростью:
, то есть с поступательным движением винта, головка которого вращается в направлении движения точки по окружности. Линейная скорость точки связана с угловой скоростью:
 .
.
В векторной форме  .
.
Если в процессе вращения угловая скорость изменяется, то возникает угловое ускорение:
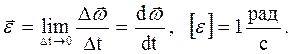
Угловое ускорение – векторная величина равная первой производной угловой скорости по времени. Вектор угловой скорости сонаправлен с вектором элементарного изменения угловой скорости  , происшедшего за время dt.
, происшедшего за время dt.
При ускоренном движении вектор 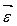 параллелен
параллелен  (рис. 8), при замедленном – противонаправлен (рис. 9).
(рис. 8), при замедленном – противонаправлен (рис. 9).


Угловое ускорение возникает в системе только тогда, когда происходит изменение угловой скорости, то есть когда линейная скорость движения изменяется по величине. Изменение же скорости по величине характеризует тангенциальное ускорение.
Найдем связь между угловым и тангенциальным ускорениями:
 .
.
Изменение направления скорости при криволинейном движении характеризуется нормальным ускорением  :
:
 .
.
Таким образом, связь между линейными и угловыми величинами выражается следующими формулами:
 .
.
Типы вращательного движения
а) переменное – движение, при котором изменяются  и
и 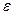 :
:

б) равнопеременное – вращательное движение с постоянным угловым ускорением:
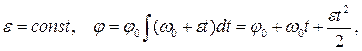
 .
.
в) равномерное – вращательное движение с постоянной угловой скоростью:
 .
.
Равномерное вращательное движение можно характеризовать периодом 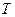 и частотой вращения
и частотой вращения  .
.
Период – это время, за которое тело совершает один полный оборот.
 , [T] = c.
, [T] = c.
Частота вращения – это число оборотов совершаемых за единицу времени.
 , [n] = c-1.
, [n] = c-1.
За один оборот:  ,
,
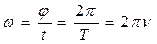 ,
, 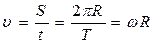 .
.
Дата добавления: 2014-12-03; просмотров: 373; Мы поможем в написании вашей работы!; Нарушение авторских прав |