
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение состояния идеального газа. Опытные газовые законы.
При сравнении законов вращательного и поступательного движений усматривается аналогия.
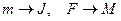 .
.
Аналогом импульса является момент импульса. Понятие момента импульса также можно ввести относительно неподвижной точки и относительно неподвижной оси, однако в большинстве случаев его можно определить следующим образом. Если материальная точка вращается вокруг неподвижной оси, то её момент импульса относительно этой оси по модулю равен

где mi - масса материальной точки,
ui - её линейная скорость
ri - расстояние до оси вращения.
Т.к. для вращательного движения

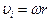 ,
,
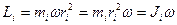 ,
,
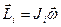 ,
,
где  - момент инерции материальной точки относительно этой оси.
- момент инерции материальной точки относительно этой оси.
Момент импульса твердого тела относительно неподвижной оси равен сумме моментов импульсов всех его точек относительно этой оси:
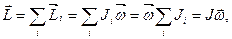
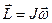 , (2)
, (2)
 где
где 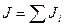 - момент инерции тела.
- момент инерции тела.
Т.о., момент импульса твердого тела относительно неподвижной оси вращения равен произведению его момента инерции относительно этой оси на угловую скорость и сонаправлен с вектором угловой скорости.
Продифференцируем уравнение (2) по времени:

или 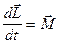 . (3)
. (3)
Уравнение (3) - ещё одна форма основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента
импульса твердого тела относительно неподвижной оси вращения равна моменту внешних сил относительно той же оси
Это уравнение является одним из важнейших уравнений ракетодинамики. В процессе движения ракеты положение ее центра масс непрерывно изменяется, вследствие чего возникают различные моменты сил: лобового сопротивления, аэродинамической силы, сил создаваемых рулем высоты. Уравнение вращательного движения ракеты под действием всех приложенных к ней моментов сил совместно с уравнениями движения центра масс ракеты и уравнениями кинематики с известными начальными условиями позволяют определить положение ракеты в пространстве в любой момент времени.
Основные положения и основные понятия МКТ.
Существуют два основных метода описания физических явлений и построения соответствующих теорий:
1) молекулярно-кинетический (статистический);
2) термодинамический.
Молекулярно-кинетический метод рассматривает свойства физических объектов как суммарный результат действия всех молекул.
Поведение отдельной молекулы анализируется на основе законов классической механики, и полученные результаты распространяются на совокупность большого числа молекул с помощью статистического метода, использующего законы теории вероятности. Это возможно, поскольку движение каждой молекулы хотя и проходит по законам классической механики, но является случайным, т.к. скорости молекул подчиняются законам теории вероятности. Чем больше частиц в системе, тем лучше совпадают выводы статистической теории с результатами эксперимента.
Преимущество метода - ясная картина механизма рассматриваемого явления.
Недостаток - выводы МК теории являются результатом усреднения, поэтому являются приближенными.
Термодинамический метод основывается на введении понятия энергии и рассматривает все процессы с энергетической точки зрения, основываясь на законах сохранения и превращения энергии из одного вида в другой.
Молекулярная физика - раздел физики, изучающий строение и свойства вещества исходя из молекулярно-кинетической теории.
Идея об атомном строении вещества высказана древнегреческим философом Демокритом (»400 г до н.э.). Как научная гипотеза теория атомизма возрождается в XVII веке и развивается в работах Ломоносова (18 век), объяснившего тепловые явления как результат движения мельчайших частиц вещества.
Основные положения МКТ базируются на ряде опытных данных и наблюдений (диффузия, броуновское движение).
1. Все вещества состоят из атомов или молекул.
2. Атомы всех веществ находятся в беспрестанном хаотическом движении.
3. Атомы (или молекулы) всех веществ взаимодействуют между собой.
Диффузия - явление проникновения молекул одного вещества между молекулами другого при их соприкосновении.
Броуновское движение – хаотическое движение взвешенных в жидкости или газе частиц.
Молекула - мельчайшая частица вещества, обладающая всеми его химическими свойствами.
mм» 10-26 кг, d» 10-10м.
Молекулярная масса - масса одной молекулы, измеряется в а.е.м.
| вещество | масса м-лы (а.е.м.) | масса вещества (г) | число молекул |
| Н2 | 6,02×1023 | ||
| С | 6,02×1023 | ||
| О2 | 6,02×1023 | ||
| СО2 | 6,02×1023 |
1 моль - это количество вещества, в котором содержится столько молекул, сколько их содержится в 12 г  - основная единица СИ.
- основная единица СИ.
Число Авогадро NА - это число молекул, содержащихся в одном моле любого вещества. Молярная масса - масса одного моля.
 ,
,
 число молей вещества,
число молей вещества,
 число молекул вещества.
число молекул вещества.
Уравнение состояния идеального газа. Опытные газовые законы.
В МКТ используют идеализированную модель идеального газа.
Идеальный газ - это газ, молекулы которого можно рассматривать как материальные точки, а их взаимодействие носит характер абсолютно упругого удара. (при низком р и высокой Т реальные газы приближаются к идеальным).
Состояние некоторой массы газа определяется тремя термодинамическими параметрами: р,V,T.
Давление газа представляет собой результат ударов молекул газа о стенки сосуда, в котором газ находится.
[р]=1Па.
[V]= 1м3.
В соответствии с решением XI Генеральной конференции по мерам и весам (1960 г.) применяют две температурные шкалы - термодинамическую (Кельвина) и Международную практическую (Цельсия).
За 0°С принята температура замерзания воды при р=1 атм. За 0 К принята температура, при которой должно прекратиться хаотическое движение молекул. Анализ различных процессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно.
Градус Кельвина равен градусу Цельсия.
Т= t°С+ 273, DT=Dt°.
Между параметрами газа существует определенная связь, называемая уравнением состояния. Уравнение, связывающее параметры состояния идеального газа, называется уравнением состояния идеального газа или уравнением Клапейрона:
 . (1)
. (1)
Для данной массы идеального газа отношение произведения давления на объем к абсолютной температуре есть величина постоянная.
Определим значение константы  для определенного количества идеального газа, а именно для одного моля.
для определенного количества идеального газа, а именно для одного моля.
Согласно закону Авогадро 1 моль любого газа при нормальных условиях (Т0=273 К, р0=105 Па) имеет VМ= 22,4×10-3 м3.
Для одного моля

 - молярная газовая постоянная.
- молярная газовая постоянная.
Для произвольной массы газа
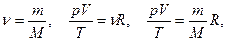
 уравнение Менделеева-Клапейрона – уравнение состояния идеального газа произвольной массы.
уравнение Менделеева-Клапейрона – уравнение состояния идеального газа произвольной массы.
Уравнение (1) объединяет в себе три частных случая, три эмпирических закона для изопроцессов, т.е. процессов, при которых один из параметров остается постоянным.
1. Т= const – изотермический процесс,
 или
или  - закон Бойля-Мариотта:
- закон Бойля-Мариотта:  для данной массы идеального газа при Т= const произведение давления на объем есть величина постоянная.
для данной массы идеального газа при Т= const произведение давления на объем есть величина постоянная.
Графики зависимости между параметрами состояния газа при Т=const представлены на рис. 1.
2.  р= const – изобарный процесс,
р= const – изобарный процесс,  или
или 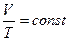
 - закон Гей-Люссака: для данной массы идеального газа при р=const объем прямо пропорционален абсолютной температуре.
- закон Гей-Люссака: для данной массы идеального газа при р=const объем прямо пропорционален абсолютной температуре.
Графики зависимости между параметрами состояния газа при р=const представлены на рис. 2.
3.  V=const – изохорный процесс,
V=const – изохорный процесс,  или
или 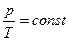 -
-
закон Шарля: для данной массы идеального газа при V=const давление прямо пропорционально абсолютной температуре.
Графики зависимости между параметрами состояния газа при V=const представлены на рис. 3.
Дата добавления: 2014-12-03; просмотров: 397; Мы поможем в написании вашей работы!; Нарушение авторских прав |