Закон Био-Савара-Лапласа и его применение для расчета магнитных полей.

Магнитное поле постоянных токов различной формы было подробно исследовано фр. учеными Био и Саваром. Ими было установлено, что во всех случаях магнитная индукция в произвольной точке пропорциональна силе тока, зависит от формы, размеров проводника, расположения этой точки по отношению к проводнику и от среды.

Результаты этих опытов были обобщены фр. математиком Лапласом, который учел векторный характер магнитной индукции и высказал гипотезу о том, что индукция в каждой точке представляет собой, согласно принципу суперпозиции, векторную сумму индукций элементарных магнитных полей, создаваемых каждым участком этого проводника.

или .

Лапласом в 1820 г. был сформулирован закон, который получил название закона Био-Савара-Лапласа: каждый элемент проводника с током (рис. 9) создает магнитное поле, вектор индукции которого в некоторой произвольной точке К определяется по формуле:

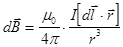- закон Био-Савара-Лапласа.

Из закона Био-Совара-Лапласа следует, что направление вектора совпадает с направлением векторного произведения . Такое же направление дает и правило правого винта (буравчика).

,

- элемент проводника, сонаправленный с током;

- радиус-вектор, соединяющий c точкой K;

a - угол между и .

Закон Био-Савара-Лапласа имеет практическое значение, т.к. позволяет найти в заданной точке пространства индукцию магнитного поля тока, текущего по проводнику конечных размеров и произвольной формы.

Для тока произвольной формы подобный расчет представляет собой сложную математическую задачу. Однако, если распределение тока имеет определенную симметрию, то применение принципа суперпозиции совместно с законом Био-Савара-Лапласа дает возможность относительно просто рассчитать конкретные магнитные поля.

Рассмотрим некоторые примеры.

Магнитное поле в центре кругового тока (рис. 10):

.

a=90⁰, sina=1, .

Магнитное поле прямолинейного проводника с током (рис. 11).

1) для проводника конечной длины (рис. 12):

;

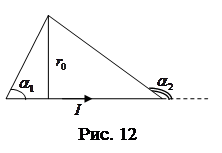
2) для проводника бесконечной длины: a₁ = 0, a₂ = p,

.