Розподіл Максвелла ― Больцмана та його аналіз

Класичний розподіл Максвелла ― Больцмана можна одержати скориставшись квантовим розподілом Фермі ― Дірака і густиною станів. Запишемо ці вирази :

(2.2.1)

де – імовірність заповнення квантових станів частинками; E – повна енергія частинок; m ― хімічний потенціал;

(2.2.2)

де 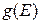― густина станів в енергетичній зоні; s ― спін мікро- частинки; р ― імпульс мікрочастинок; dV – об’єм мікростану в просторі координат; – похідна імпульсу за енергією; h – стала Планка.

Якщо Т >> 0, то >>1. В цьому випадку формула (2.2.1) переписується так:

(2.2.3)

Повну енергію Е в цьому випадку виразимо через кінетичну енергію e і потенціальну енергію U, тобто

(2.2.4)

З урахуванням (2.2.4) вираз (2.2.3) матиме вигляд

(2.2.5)

Знайдемо число частинок в системі, скориставшись таким співвідно-шенням

(2.2.6)

де А – деяка константа; g(E) – густина станів в енергетичній зоні; f(E) – імовірність заповнення цих станів мікрочастинки; dE – ширина енергетичного інтервалу.

Підставимо в (2.2.6) значення g(E) і f(E), одержимо

(2.2.7)

де враховано, що .

З правого боку виразу (2.2.7) чітко спостерігається поділ на дві частини, одна з яких залежить лише від потенціальної енергії частинок системи, а друга лише від кінетичної енергії. Вираз (2.2.7) називають класичним розподілом Максвелла ─ Больцмана.