
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Помилки вибірки.
Відхилення узагальнених показників вибіркової сукупності від зведених характеристик генеральної сукупності називається помилками вибірки, вони виникають внаслідок самого факту відбору. Структура вибіркової сукупності не може точно відтворити генеральну сукупність. Помилки властиві вибірковому спостереженню називаються помилками вибірки, або репрезентативності. За своєю природою вони можуть бути систематичними і випадковими.
Систематичні помилки вибіркивиникають при порушенні принципів проведення вибіркового спостереження. Наприклад, якщо при обстеженні успішності студентів відібрати для спостереження сильну групу, то середній бал буде завищений.
Систематичні помилки спрямовані тільки в один бік (або зменшення, або збільшення) і призводять до того, що вибіркове спостереження втрачає свій сенс, тому що на його основі не можна правильно визначити показники генеральної сукупності. Систематичних помилок можна уникнути. Для попередження й усунення їх потрібно встановити науково обґрунтований порядок відбору, який проводиться випадковим методом, коли кожній одиниці генеральної сукупності забезпечена однакова можливість потрапити у вибірку.
Якщо відбір зроблено правильно, то розбіжності між узагальненими показниками вибіркової і генеральної сукупностей виникають через сам факт відбору і називаються випадковими помилками вибірки.
Випадкові помилки дають відхилення як в один, так і в інший бік. Вони властиві вибірковому спостереженню, усунути їх практично неможливо, але можна обчислити.
Помилка вибірки залежить від чисельності вибіркової сукупності і ступеня варіації досліджуваної ознаки. Чим більше одиниць відібрано у вибіркову сукупність, тим меншими, за інших рівних умов, будуть розбіжності. Чим менша варіація ознаки, тим менша помилка вибірки.
В математиці було доведено, що
при повторному відборі при безповторному відборі



де μ – середня похибка вибірки; σ2 – дисперсія ознаки в генеральній сукупності; n – число одиниць вибіркової сукупності; N – число одиниць генеральної сукупності; w – частка одиниць, що мають певні ознаки.
Із наведених формул впливає, що похибка репрезентативності залежить від багатьох чинників: ймовірності, з якою ми бажаємо отримати результат; кількості одиниць вибіркової сукупності (чим менше одиниць складатиме вибіркова сукупність, тим більше буде похибка репрезентативності, і навпаки); однорідності досліджуваної сукупності (чим більше різнорідною є сукупність, тим більше буде похибка репрезентативності) і від способу відбору одиниць у вибіркову сукупність.
Для визначення середньої помилки вибірки потрібно знати дисперсію ознаки в генеральній сукупності. Але при вибірковому спостереженні генеральна дисперсія невідома.
У курсі математичної статистики доведено, що
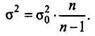
У міру зростання числа вибірки коефіцієнт 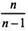 наближається до одиниці і розбіжності між генеральною і вибірковою дисперсіями стають меншими. Тому середню помилку вибірки можна обчислити, виходячи зі значення вибіркової дисперсії.
наближається до одиниці і розбіжності між генеральною і вибірковою дисперсіями стають меншими. Тому середню помилку вибірки можна обчислити, виходячи зі значення вибіркової дисперсії.
Середня помилка вибірки характеризує міру відхилень вибіркової середньої від генеральної середньої, частки вибіркової від частки генеральної.
Розраховану за вказаними формулами помилку вибірки дає можливість стверджувати, що показник вибіркової сукупності будуть відрізнятися від показників генеральної сукупності на розраховану величину з імовірністю 0,683, тобто якщо буде відібрано 1000 одиниць сукупності, то 683 із них матимуть дану ознаку. Точність розрахунку можна гарантувати на 68,3 %.
Розраховані з імовірністю 0,683 показники не завжди влаштовують дослідників. Щоб підвищити ймовірність, потрібно розширити межі відхилень і вводиться довірчий коефіцієнт t. Середня помилка вибірки помножена на довірчий коефіцієнт називається граничною помилкою вибірки.
Отже, гранична помилка вибірки розраховується за такою формулою:
 ,
,
де Δ – похибка вибірки, тобто похибка репрезентативності;
μ – середня похибка вибірки;
t – коефіцієнт, що залежить від ймовірності, з якою можна гарантувати певний розмір похибки репрезентативності.
Коефіцієнт довіри залежить від імовірності, з якою можна гарантувати, що гранична помилка вибірки не перевищить t-кратну середню помилку. Коефіцієнт t визначається за таблицями значень інтеграла ймовірностей. Так, при
t=0, то ймовірність також дорівнює 0.
t=0,5, то ймовірність також дорівнює 0,383.
t=1, то ймовірність також дорівнює 0,683.
t=2, то ймовірність також дорівнює 0,954.
t=3, то ймовірність також дорівнює 0,997.
t=4, то ймовірність також дорівнює 0,999936. і т.д.
Багаторічна практика свідчить про те, що довірча ймовірність 95,4 % (для t=2) є оптимальною для більшості розрахунків у різних галузях господарства, тим більше для правових явищ.
Показники генеральної сукупності відрізняються від показників вибіркової сукупності на величину похибки репрезентативності
середня –  =
=  ± Δ,
± Δ,
частка – W = w ± Δ,
де Δ – гранична похибка репрезентативності;
 – середня генеральної сукупності;
– середня генеральної сукупності;
 – середня вибіркової сукупності;
– середня вибіркової сукупності;
W – питома вага одиниць, які мають якусь альтернативну ознаку (частка) в генеральній сукупності;
w – питома вага одиниць, які мають якусь альтернативну ознаку (частка) в вибірковій сукупності.
Наведені формули помилок вибірки дають змогу заздалегідь розрахувати той обсяг вибірки, при якому відхилення вибіркових показників від генеральних не перевищать заздалегідь заданих розмірів, що гарантуються з визначеною ймовірністю.
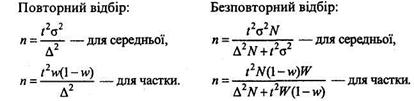
Дата добавления: 2014-12-03; просмотров: 421; Мы поможем в написании вашей работы!; Нарушение авторских прав |