Магнітний потік. Теорема Гауса для магнітного поля

Магнітним потоком через елементарну площадку називається фізична величина, що дорівнює скалярному добутку вектора магнітної індукції та площі площадки:

, (4.33)

де – проекція 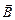на нормаль до площадки; 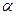– кут між векторами 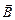та (рис.4.17).

Якщо врахувати правила побудови ліній магнітної індукції (див. §4.1), то стає очевидним фізичний зміст магнітного потоку: він чисельно дорівнює кількості ліній магнітної індукції, що перетинають дану площадку. Магнітний потік через довільну поверхню знайдемо інтегруванням (4.33) по площі поверхні:

. (4.34)

Зокрема, для плоскої поверхні в однорідному магнітному полі

. (4.35)

В СІ одиницею вимірювання магнітного потоку є вебер:

.

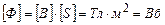Магнітний потік може бути як додатнім, так і від’ємним, в залежності від знаку (визначається позитивним напрямком нормалі ).

Теорема Гауса для магнітного поля: магнітний потік через будь-яку замкнену поверхню дорівнює нулю:

. (4.36)

Ця теорема є наслідком того, що в природі не існує «магнітних зарядів», лінії магнітної індукції не мають ні початку, ні кінця (див. §4.1), тому число ліній, що входять в довільну замкнену поверхню, дорівнює числу ліній, що виходять з неї.