Корпускулярно-хвильовий дуалізм матерії; гіпотеза де Бройля. Співвідношення невизначеностей Гайзенберга

7.2.1. Як показано в розділі 6, світло володіє як хвильовими, так і корпускулярними властивостями. Луї де Бройль (1924 рік) висунув гіпотезу (постулат) про те, що корпускулярно-хвильовий дуалізм притаманний не тільки світлу, але матерії взагалі: усяка частинка, яка має імпульс 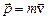і енергію Е, володіє хвильовими властивостями, її рух супроводжується хвильовим процесом з довжиною хвилі де-Бройля

(7.11)

та частотою

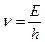. (7.12)

В залежності від величини швидкості v (кінетичної енергії 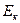) частинок, їх імпульс розраховується або за класичною формулою (при )

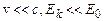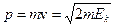, (7.13)

або за релятивістською формулою (при 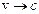, Е_k співмірна з Е₀)

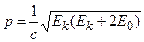, (7.14)

де m – маса частинки (таблична величина), – її енергія спокою.

Зокрема, вільна частинка, що рухається вздовж осі х, описується плоскою хвилею де Бройля

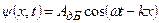, (7.15)

де – амплітуда хвилі де Бройля, 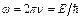– її циклічна частота, 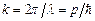– її хвильове число. Фазова швидкість хвиль де Бройля

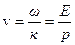, (7.16)

а групова швидкість

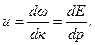(7.17)

Борівське квантування моменту імпульсу орбітального руху електрона набуває нового змісту з врахуванням хвильових властивостей електрона. Зокрема, довжина стаціонарної орбіти

,

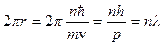тобто в межах орбіти вкладається ціле число хвиль де Бройля.

Оцінимо довжину хвилі де Бройля електрона, який прискорився електричним полем 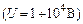. Саме такі напруги використовуються у вакуумних електронних приладах (радіолампи, рентгенівські трубки тощо). Підставляючи в формулу (7.13) значення кінетичної енергії електронів 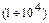еВ, отримаємо за (7.11) для довжин хвиль де Бройля нм.

Відомо, що найбільш чітко хвильові властивості світла проявляються в явищі дифракції. І тому прояв хвильових властивостей електронних (нейтронних, атомних тощо) пучків слід очікувати в цьому ж явищі. При цьому чітка дифракційна гратка спостерігається тоді, коли довжини хвиль співмірні з розміром дифракційної неоднорідності (отвори, щілини тощо).

Розміри макроприладів значно перевищують довжини хвиль де Бройля електронів, і тому в цьому випадку хвильові властивості електронів явно не відслідковуються. В цей же час розраховані значення l співмірні з розміром ( 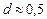нм) кристалічної гратки твердих тіл. І тому така гратка повинна бути дифракційним пристроєм для електронних пучків. Дійсно, при проходженні електронних пучків через тонкі полікристалічні плівки та при їх відбиванні від монокристалів спостерігається така ж дифракційна картина, як і при взаємодії рентгенівських променів з твердими кристалічними тілами. Зокрема, виконується закон Вульфа-Бреггів (див. розділ 6), встановлений для рентгенівських променів. Дифракція нейтронних пучків також виявлена експериментально і використовується для наукових досліджень.

Відмітимо, що довжини хвиль де Бройля макроскопічних тіл, за рахунок великої маси, настільки малі, що їх хвильові властивості виявити неможливо.

7.2.2. Корпускулярно-хвильовий дуалізм частинок в мікросвіті накладає обмеження на можливості класичного опису їх стану. В класичній механіці стан частинки задається сукупністю точно заданих координат (x,y,z) та проекцій вектора імпульсу 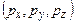. Якщо задані сили, що діють на частинку, то можна, користуючись законами класичної механіки, передбачити її стан в довільний момент часу – класичний принцип причинності. Для частинки, що рухається вздовж осі х, це означає, що неточності (невизначеності) координати 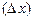та імпульсу 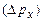рівні нулю і добуток .

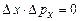Абсолютно інша ситуація в мікросвіті. Дійсно, вільна частинка, яка рухається вздовж осі х, описується плоскою монохроматичною хвилею де Бройля (7.15), де 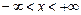. І тому її положення повністю невизначене, тобто 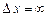. З іншого боку, імпульс такої частинки 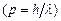строго визначений і 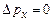. А отже, добуток 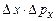є математично невизначеним .

В мікросвіті можна змоделювати об’єкти (наприклад, хвильовий пакет), для яких координата точно визначена , але імпульс повністю невизначений 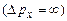, і тому має місце математична невизначеність типу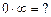

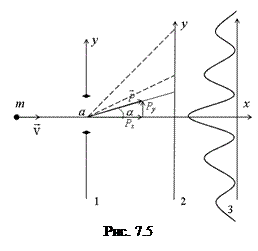
Для того, щоб дещо прояснити цю ситуацію, розглянемо наступний умовний експеримент (рис. 7.5). Нехай мікрочастинки, що рухаються вздовж осі х, пролітають через щілину шириною а в непрозорому екрані (1) і фіксуються на екрані спостереження (2). Після проходження щілини розподіл мікрочастинок вздовж осі у повинен відтворювати розподіл інтенсивності в дифракційній картині (3): центральний і бічні максимуми розділені мінімумами. До щілини невизначеності координати та імпульсу: , 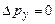. В момент проходження щілини: 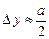, 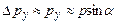. Якщо розглядати лише мікрочастинки, які попадають в центральний максимум, що обмежений першими мінімумами, то 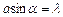, і тому 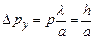. Добуток невизначеностей:

.

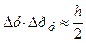На підставі аналізу подібних умовних експериментів Гайзенберг (1927р.) встановив співвідношення між невизначеностями координат і відповідних імпульсів у вигляді

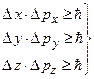. (7.18)

Інтерпретацію цих співвідношень дав Н. Бор у вигляді принципу доповнюваності:

1) інформація про стан мікрочастинок може бути отримана лише за допомогою макроприладів, які взаємодіють з мікрочастинками;

2) за допомогою конкретного макроприладу можна встановити точне значення або координати, або імпульсу; при цьому чим точніше задана одна характеристика, тим більш невизначена інша.

Стосовно електрона в атомі співвідношення Гейзенберга означають, що поняття орбіти втрачає зміст. Дійсно, якщо невизначеність швидкості електрона , то невизначеність координати , що співмірно з розміром атома. Таким чином, електрон “розмазаний” по всьому об’ємі атома. В цей же час співвідношення невизначеностей не накладають суттєвих обмежень на класичний опис стану макротіл. Дійсно, оскільки 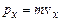, то 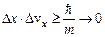навіть при .

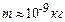Пара “координата-імпульс” у співвідношенні (7.18) не є випадковою, оскільки вона входить як добуток в рівняння плоскої хвилі де Бройля (7.15), записане у вигляді

. (7.19)

І тому слід очікувати, що і для іншої пари “енергія-час” матиме місце співвідношення невизначеностей

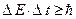, (7.20)

де має зміст тривалості перебування (часу життя) мікрочастинки в певному стані. Зокрема, для основного стану електрона у воднеподібному атомі і тому 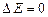, тобто енергетичний рівень основного стану нерозмитий. Для збуджених станів 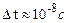і 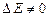. За рахунок цього спектральні лінії випромінювання не є строго монохроматичними.