Хвильова функція та її зміст. Рівняння Шрьодінгера

7.3.1. Корпускулярно-хвильовий дуалізм матерії встановлює межі застосування класичної фізики. В мікросвіті класичний спосіб опису стану частинок за допомогою координат та імпульсів перестає бути однозначним і повинен бути замінений іншим – статистичним способом, на якому грунтується механіка мікросвіту – квантова механіка.

Стан мікрочастинок в квантовій механіці задається хвильовою функцією . Зокрема, для вільної одновимірної частинки хвильовою функцією є плоска хвиля де Бройля (7.19), яку представимо тут у комплексній формі:

, (7.21)

де . Помноживши на комплексно спряжену функцію , отримаємо

. (7.22)

З точки зору хвильових уявлень квадрат амплітуди хвилі визначає її інтенсивність, зокрема, інтенсивність дифракційних максимумів на рис. 7.5. З точки зору корпускулярних уявлень – це імовірність попасти мікрочастинці в ту чи іншу точку екрану спостереження після проходження щілини. Отже, фізичний зміст має не сама хвильова функція, а вираз , який називається густиною імовірності. Для частинок, які не є вільними, а перебувають в силових полях, хвильова функція не може розглядатися як просторова хвиля, але її ймовірнісна інтерпретація залишається в силі. Зокрема, імовірність знайти мікрочастинку в деякій області простору, наприклад, в елементарному об’ємі , становить

. (7.23)

Оскільки імовірність повинна бути однозначною, неперервною і скінченою, то на хвильову функцію накладаються наступні стандартні вимоги:

1) вона повинна бути однозначною, неперервною і скінченою;

2) перші похідні по координатах і часу від хвильової функції також повинні бути неперервними, що забезпечить “гладкість” імовірності;

3) вона повинна бути інтегрованою; зокрема, , як імовірність знайти частинку в будь-якій точці простору V (імовірність вірогідної події).

Знання хвильової функції дозволяє встановити середнє значення довільної фізичної величини f:

. (7.24)

Для знаходження хвильової функції конкретного квантовомеханічного об’єкту необхідно розв’язати рівняння Шрьодінгера (1926 р.)

, (7.25)

яке є аналогом ІІ закону Ньютона класичної механіки. В цьому рівнянні

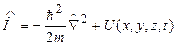– (7.26)

оператор Гамільтона або оператор повної енергії частинки, де m – маса частинки, – оператор Лапласа

, (7.27)

U – оператор потенціальної енергії, дія якого зводиться до простого множення на хвильову функцію.

Якщо потенціальна енергія частинки явно не залежить від часу, тобто , то квантовомеханічна задача називається стаціонарною, і у хвильовій функції можливе розділення змінних, тобто

. (7.28)

Підставляючи (7.28) у (7.25), після нескладних перетворень отримаємо

, (7.29)

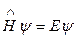, (7.30)

де с і Е – константи інтегрування, при цьому Е має зміст енергії частинки.

Рівняння (7.30) називається рівнянням Шрьодінгера для стаціонарних станів. Розв’язок цього диференціального рівняння задовольняє стандартні вимоги до хвильової функції, як правило, не при усяких, а дискретних (дозволених) значеннях параметра Е. Ці значення називаються власними значеннями оператора , а відповідні хвильові функції – власними функціями цього оператора.

Отже, розв’язок рівняння Шрьодінгера (7.30) зводиться до знаходження власних значень і власних функцій оператора повної енергії частинки . При цьому дискретність (квантування) енергії не вимагає додаткових штучних припущень типу постулатів Бора (§7.1), а витікає з математичних властивостей самого рівняння Шредінгера. Фізична ж суть цього рівняння полягає у виборі аналітичної форми потенціальної енергії U, тобто у виборі моделі квантомеханічного об’єкту.

7.3.3. Для вільної (U=0) частинки, що рухається вздовж осі х, стаціонарне рівняння Шрьодінгера має вигляд

.

Розв’язок цього рівняння шукається у вигляді

,

що легко перевірити підстановкою в рівняння Шрьодінгера.

Повна хвильова функція, з врахуванням (7.28) і (7.29),

співпадає з виразом для плоскої хвилі де Бройля (7.19), якщо покласти, що 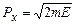. Остання рівність є очевидною, оскільки повна енергія частинки співпадає з її кінетичною енергією

. (7.31)