Магнітний момент атомів. Досліди Штерна і Герлаха. Власний момент електрона (спін). Ферміони і бозони

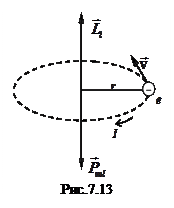7.7.1. Користуючись формальним поняттям орбіти електрона, орбітальний рух електрона (рис.7.13) можна розглядати як коловий струм, що володіє магнітним моментом

де –частота обертання електрона, –маса електрона.

Оскільки механічний і магнітний моменти, як видно з рис.7.13, напрямлені протилежно, то остаточно

. (7.54)

Якщо атом перебуває в магнітному полі з індукцією 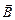, то проекція магнітного моменту орбітального руху на напрямок поля, з врахуванням (7.49),

, (7.55)

де – магнетон Бора. Отже, ми приходимо до квантування проекції магнітного моменту на напрямок поля; звідси стає зрозумілою назва квантового числа . Магнітний момент атома шукається як векторна сила магнітних моментів усіх електронів ( ) і може бути як рівним нулю (діамагнітні атоми), так і відмінним від нуля (парамагнітні атоми).

7.7.2. Для експериментального визначення магнітних моментів атомів Штерн і Герлах (1921 р.) пропускали у вакуумі вузькі атомні пучки через сильно неоднорідне магнітне поле (рис.7.14). В такому полі на атом з магнітним моментом 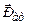діє відхиляюча сила

,

де – градієнт магнітного поля вздовж осі z, а – проекція магнітного моменту атома на напрямок поля. У відсутності квантування РП фіксував би неперервний розподіл атомів, оскільки значення були б довільними. В дійсності спостерігається розщеплення атомних пучків на декілька, симетричних відносно осьової лінії ДО, що свідчить про наявність просторового квантування. Але деталі експерименту не зовсім узгоджувались з теорією.

Зокрема, в атомах срібла магнітний момент повинен визначатися лише одним валентним електроном, який в умовах експерименту перебуває в s-стані . А це означає, що для срібла Р_ат = 0, і розщеплення атомного пучка не слід очікувати, що суперечить експерименту.

7.7.3. Додаткову інформацію про магнітні параметри електронів атомів дають дослідження впливу магнітного поля на спектри випромінювання. Для прикладу розглянемо спектральну лінію, зумовлену переходом електрона з 2р-стану в 1s-стан атома водню (рис. 7.15). Якщо випромінюючий атом перебуває в магнітному полі, то електрон набуває додаткової енергії

. (7.56)

Оскільки у 2р-стані 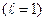магнітне квантове число набуває значення 0, , то в магнітному полі енергетичний рівень цього стану розщеплюється на три рівні, тобто виродження по знімається. І в спектрі випромінювання замість однієї спектральної лінії з частотою з’являються три лінії з частотами , і , де – “нормальне” лоренцове зміщення. Розщеплення спектральних ліній випромінювання атомів в магнітному полі називається ефектом Зеемана. Але лише для не багатьох спектральних ліній деяких атомів спостерігається “нормальний” ефект Зеемана, коли експеримент узгоджується з викладеною теорією. В більшості випадків має місце “аномальний” ефект , коли характер розщеплення як якісно, так і кількісно інший, ніж це передбачено теорією.

7.7.4 Для пояснення дослідів Штерна і Герлаха, “аномального” ефекту Зеемана, а також спектрів випромінювання складних атомів необхідно було ввести ще одне квантове число електрона. І тому Гоудсміт і Уленбек (1925 р.) висунули гіпотезу про те, що електрон володіє власним моментом імпульсу, не пов’язаним з його просторовим рухом,

, (7.57)

де s – спінове квантове число, яке для електрона дорівнює 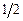. З цим моментом пов’язаний власний магнітний момент

. (7.58)

Проекції цих моментів на вибраний напрямок (вісь z)

,

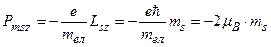, (7.59)

де – магнітне спінове квантове число електрона. Отже, в дослідах Штерна і Герлаха атоми срібла можуть мати два значення проекції магнітного моменту на напрямок магнітного поля , і тому атомний пучок розщеплюється на два симетричних , що спостерігається експериментально (рис.7.14).

7.7.5 Пізніше виявилось, що власний (спіновий) рух притаманний усім мікрочастинкам (атомам, ядрам, протонам, нейтронам тощо). Спін – така ж характеристика мікрочастинок як маса і заряд. Наявність спіну випливає з розв’язку релятивістського аналогу рівняння Шрьодінгера – рівняння Дірака. В залежності від значення квантового числа s усі мікрочастинки поділяються на ферміони – частинки з напівцілим спіном і бозони – частинки з цілочисельним спіном . До ферміонів належать електрони, протони, нейтрони, до бозонів – фотони, 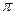-мезони. Атоми та ядра можуть бути як ферміонами, так і бозонами. Поділ мікрочастинок на ферміони і бозони є наслідком принципу квантової нерозрізняльності тотожних частинок, що для системи з двох тотожних частинок дає , тобто густина імовірності не змінюється при перестановці частинок місцями (тут х_i–сукупність просторових і спінових координат і-тої частинки). Звідси можливі два варіанти:

– симетрична хвильова функція;

– антисиметрична хвильова функція.

Бозони описуються симетричними, а ферміони – анти-симетричними хвильовими функціями.