Енергія молекул. Молекулярні спектри

Молекула, як система ядер і електронів, може здійснювати наступні рухи: поступальний, обертальний, коливальний, електронний, ядерний. Якщо в першому наближенні ці рухи вважати незалежними, то енергія молекул запишеться як

. (7.63)

Оскільки енергія поступального руху не квантується, то вона нас цікавити не буде. Ядерна енергія квантується, але відстані між ядерними енергетичними рівнями настільки великі (див. розділ 8), що у звичайних умовах енергія ядерного руху залишається незмінною. І тому в подальшому Е_пост та Е_яд у виразі (7.63) опускатимемо.

7.10.1. При утворенні молекул з окремих атомів зв’язок між ними забезпечується не всіма електронами, але лише валентними. І тому зміна електронної енергії молекул зумовлена зміною стану валентних електронів. Обмежимось розглядом двохатомних молекул (наприклад, NaCl і H₂). У випадку молекули NaCl атом Na легко іонізується і валентний електрон переходить до атома Cl. Таким чином, маємо справу з двома протилежно зарядженими іонами: Na⁺ і . Зв’язок в молекулах такого типу називають іонним або гетерополярним. Зрозуміло, що одночасно з силами кулонівського притягання існують і сили відштовхування між атомами (особливо сильні на малих відстанях). І тому потенціальна енергія взаємодії атомів в залежності від відстані має вигляд потенціальної ями.

У випадку молекули H₂ обидва валентних електрони належать одночасно обом атомам (ядрам). Розв’язок рівняння Шредінгера для такої системи (Гайтлер і Лондон, 1927р.) дає для електронної енергії молекули вирази

(7.64)

де Е₀ – енергія електрона в ізольованому атомі, К – кулонівський інтеграл, який враховує попарну кулонівську взаємодію усіх частинок системи, S – інтеграл перекриття, який враховує перекриття хвильових функцій обох електронів, А – обмінний інтеграл, який враховує нерозрізняльність електронів, що ніби "належать" то одному, то іншому атому. Таким чином, електронний рівень ізольованого атому в молекулі зазнає розщеплення (рис. 7.17, а). При цьому кожному з розв’язків (7.64) відповідає свій просторовий розподіл густини електронного заряду (рис. 7.17, б).

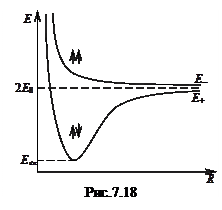
Оскільки за рахунок коливального руху атомів відстань між ними (R) змінюється, то слід очікувати залежність електронної енергії від R (рис. 7.18). Важливо відмітити, що стан з енергією Е_– реалізується при паралельній (↑↑) орієнтації спінів електронів, а стан з енергією Е₊ - при антипаралельній (↑↓) орієнтації спінів. Зрозуміло, що тільки залежність Е(R) з мінімумом відповідає стійкому стану молекули. Зв’язок в молекулах, який забезпечується антипаралельними (спареними) спінами електронів, називають ковалентним або гомеополярним.

7.10.2. Розглядаючи двохатомну молекулу як квантовий лінійний гармонічний осцилятор (§7.5), енергію коливального руху молекули запишемо як

, (7.65)

де 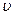= 0,1,2, … – коливальне квантове число.

Кожний електронний рівень (електронна конфігурація) має свою сукупність коливальних рівнів (рис. 7.19). Формула (7.65) справедлива лише при малих значеннях 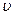, коли крива Е(R) близька до параболи. При великих інтенсивностях коливального руху (великих 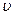) потрібно врахувати відхилення від гармонічності (ангармонізм), і енергія коливального руху молекули запишеться як

,

де γ – коефіцієнт ангармонічності. Зрозуміло, що в цьому випадку коливальні енергетичні рівні вже не є еквідистантними, а згущуються.

7.10.3. Енергія обертального руху двохатомної молекули

(7.66)

де I – момент інерції молекули відносно осі обертання, що перпендикулярна до лінії, яка сполучає атоми, і проходить через центр молекули; - кутова швидкість обертання молекули; – момент імпульсу молекули. Останній квантується так, як і орбітальний момент імпульсу електрона в атомі (7.48), тобто

(7.67)

де J = 0,1,2,3, … – обертальне квантове число.

Підставивши (7.67) у (7.66), отримаємо

. (7.68)

Момент інерції молекули розраховується як

,

де – зведена маса молекули, атоми якої мають маси m₁ та m₂ ; d – відстань між центрами атомів.

7.10.4.Підставляючи у (7.63) вирази (7.65) і (7.68), отримаємо повну енергію молекули (в гармонічному наближенні):

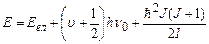. (7.69)

При цьому між енергіями різних форм руху молекули мають місце наступні нерівності: 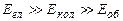. Енергетична діаграма, які відповідає виразу (7.69), для двох електронних конфігурацій представлена на рис. 7.20. Видно, що для відстаней між енергетичними рівнями різних форм руху також мають місце нерівності: Якщо певним (тепловим, оптичним тощо) чином перевести молекулу в збуджений стан, то при переході на нижчі рівні будуть випромінюватись кванти світла різної енергії. Але, як правило, досліджуються не спектри випромінювання, а спектри поглинання. Зумовлено це тим, що при помірних температурах молекули перебувають переважно у найнижчих електронних і коливальних станах. І тому спектри випромінювання мають мало ліній слабкої інтенсивності. Зрозуміло, що такі обмеження не поширюються на спектри поглинання, які формуються при переході з нижчих на вищі рівні під дією світла.

Розрізняють наступні типи спектрів поглинання молекул: обертальні (І), коливально-обертальні (ІІ) і електронно-коливально-обертальні (ІІІ) (рис. 7.20). Обертальні спектри виникають при переходах між обертальними рівнями молекули однієї електронно-коливальної конфігурації; при цьому виконуються правила відбору . Енергія поглинутих фотонів

(7.70)

а їх частота .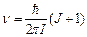

Остання формула дозволяє за експериментальними значеннями частот (довжин хвиль) обертального спектру визначати момент інерції молекул. Відмітимо, що обертальні спектри лежать у далекій інфрачервоній області (l = 10^-4¸10^{-3 м}), на межі з ультрарадіодіапазоном.

Коливально-обертальні спектри формуються при переходах між обертальними рівнями молекули в різних коливальних конфігураціях, але однієї електронної конфігурації; при цьому виконуються наступні правила відбору: Du = ±1, DJ = ±1. Енергія поглинутих фотонів (для малих u, коли справедлива формула(7.65))

(7.71)

а частота .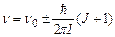

Такий спектр являє собою смугу близьких ліній, розміщених симетрично відносно уявної v₀‑лінії, яка не реалізується. Зрозуміло, що остання формула дозволяє встановити як момент інерції молекули, так і частоту її власних коливань. Коливально-обертальні смуги лежать в середній ІЧ-області (l » 10^{-5 м}).

Електронно-коливально-обертальні спектри поглинання формуються при переходах між обертальними рівнями молекули в різних електронних конфігураціях; при цьому виконуються правила відбору: Du = ±1, DJ = 0, ±1. Отже, кожній парі електронних рівнів відповідає група смуг коливально-обертального спектру. Ці смуги лежать як у близькій ІЧ-області, так і у видимій області (l £ 10^{-6 м}).

 

 

---

Дата добавления: 2014-12-03; просмотров: 109; Нарушение авторских прав

---

⇐ Предыдущая118119120121122123124125126127Следующая ⇒