Теплові коливання кристалічної решітки і теплоємність твердих тіл

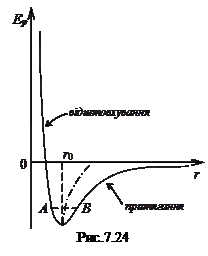7.13.1.Більшість твердих тіл володіють кристалічною структурою, тобто є сукупністю великого числа атомів, впорядковано розміщених в просторі, і які тим самим утворюють кристалічну решітку. Оскільки атоми, що перебувають в сусідніх вузлах кристалічної решітки, зазнають взаємного притягання і відштовхування, то потенціальна енергія взаємодії між ними має вигляд потенціальної ями (рис.7.24).

В рамках класичної фізики при 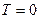атоми повинні перебувати на дні потенціальної ями, на відстані r₀ один від одного. І, звичайно, бути нерухомими. З підвищенням температури енергія атомів зростає, і кожен атом починає здійснювати коливний рух відносно рівноважного положення між точками А і В. При дуже низьких температурах ці коливання можна вважати гармонічними, бо залежність Е_р(r) – приблизно параболічна. При вищих температурах, як видно з рис. 7.24, з’являється асиметрія відхилень від рівноважного положення r₀: коливання стають ангармонічними. За рахунок ангармонізму середня відстань між атомами (штрих-пунктир) з ростом температури збільшується – має місце теплове розширення твердих тіл.

Оскільки три взаємноперпендикулярні напрямки коливань є рівноправними, то можна вважати, що атом у кристалічній решітці володіє трьома коливальними ступенями вільності (і = 3). Якщо знехтувати ефектом ангармонізму, то теплові коливання окремого атома можна моделювати сукупністю трьох незалежних лінійних осциляторів. Будемо вважати коливання окремих атомів незалежними. Тоді для одного моля речовини кількість ступенів вільності коливального руху складатиме 3N_A, де N_A – число Авогадро. В класичній фізиці на одну ступінь вільності коливального руху припадає енергія k₀Т, де k₀ – постійна Больцмана. Отже, внутрішня енергія моля твердого тіла

, (7.79)

де R – універсальна газова стала.

Молярна теплоємність тіла

. (7.80)

Такий результат (закон Дюлонга-Пті) підтверджується експериментально для багатьох простих кристалічних речовин при високих температурах. Але при низьких температурах експеримент (рис.7.25) і класична теорія катастрофічно розходяться. Зокрема, при дуже низьких температурах виконується “закон кубів Дебая” , у відповідності з яким .

7.13.2.Першу спробу узгодити експеримент з теорією здійснив А. Ейнштейн (1907 р.), який залишивши тезу про незалежність осциляторів, запропонував вважати останні не класичними, а квантовими. Як показано в §7.5, енергія квантового лінійного осцилятора

.

Ейнштейн припустив, що всі осцилятори коливаються з однаковою частотою 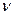, а їх розподіл за енергією описується класичною функцією розподілу Максвелла-Больцмана

,

де N₀ – загальна кількість осциляторів, а – кількість осциляторів, коливна енергія яких складає e_u. Тоді середня енергія одного осцилятора, тобто енергія, що припадає на одну ступінь вільності,

. (7.81)

Після математичних перетворень останній вираз запишеться як

. (7.82)

Внутрішня енергія одного моля твердого тіла

,

а молярна теплоємність

. (7.83)

При високих температурах, коли k₀Т>>hn, формула (7.83) дає , тобто закон Дюлонга-Пті. При низьких температурах, коли k₀Т<<hn, отримаємо

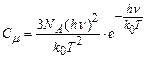. (7.84)

Оскільки експоненційна залежність сильніша від степеневої, то (7.84) дає зменшення теплоємності з пониженням температури, що лише якісно узгоджується з експериментом (рис. 7.25), але не забезпечує кількісно виконання “закону кубів Дебая”. Для розділення областей високотемпературного і низькотемпературного наближень вводиться характеристична температура Ейнштейна Q_E, при якій k₀Q_E = hn; звідси 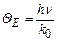. Отже, при T >> Q_E виконується закон Дюлонга-Пті; при T << Q_E виконується залежність (7.84).

7.13.3Подальше удосконалення теорії, здійснене Дебаєм (1912 р.), полягає в тому, що коливання атомів кристалічної гратки вже не вважаються незалежними, а в кристалі встановлюється система т.з. нормальних коливань з частотою від 0 до ; при цьому в коливанні певної частоти беруть участь усі атоми ґратки. Розрахунок дає для кількості нормальних коливань, частоти яких лежать в межах від n до n+dn, в одному молі речовини

. (7.85)

Поява максимальної частоти зумовлена тим, що загальна кількість нормальних коливань повинна дорівнювати кількості ступенів вільності коливного руху атомів моля кристалу, тобто

Розглядаючи кожне нормальне коливання як квантовий лінійний осцилятор, для внутрішньої енергії одного моля кристалу отримаємо

,

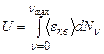а після підстановки формул (7.81) та (7.85) і математичних перетворень

. (7.86)

Ввівши підстановку 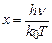, отримаємо вираз для молярної теплоємності кристалу

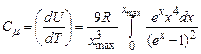. (7.87)

За аналогією з попереднім введемо характеристичну температуру Дебая Q_Д, використавши співвідношення 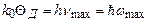; звідси

.

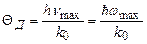Оскільки , то (7.87) після інтегрування набуде вигляду

.

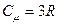При високих температурах (Т >> Q_Д), коли x®0, використавши наближення , отримаємо , тобто закон Дюлонга-Пті. При низьких температурах (Т << Q_Д), коли x_max®¥, отримаємо “закон кубів Дебая”

, (7.88)

який кількісно узгоджується з експериментом (рис.7.25).

В рамках концепції корпускулярно-хвильового дуалізму речовини зміну енергії коливного руху кристалічної гратки можна описати процесами випромінювання чи поглинання особливої квазічастинки – фонона, який володіє нульовим спіном і тому належить до класу бозонів (§7.7) .