Рівняння дотичної площини та нормалі.

1. Розглянемо поверхню другого порядку , задану рівнянням

, (1)

де - деякі дійсні числові коефіцієнти, причому коефіцієнти одночасно не дорівнюють нулю.

Доданки називають групою старших членів, або квадратичною формою, вираз - лінійною частиною, число - вільним членом рівняння.

Рівняння (1) називають загальним рівнянням поверхні другого порядку, оскільки з нього можна отримати будь-яке конкретне рівняння другого порядку. З поверхнями, рівняння яких є частинними випадками рівняння (1), ми уже зустрічалися в попередніх лекціях. Такими є сфера із центром у точці із радіусом , еліпсоїд , одно- та двопорожнинні гіперболоїди , еліптичний та гіперболічний параболоїди та інші. Природно виникає питання, чи всі можливі поверхні другого порядку ми розглянули? Приклад поверхні, яка задається рівнянням , показує, що ні. Справді, записавши дане рівняння у виді , бачимо, що його не задовольняють координати жодної точки. Можна навести також інші приклади рівнянь поверхонь, які ми ще не розглядали.

Оскільки рівняння (1) містить 10 коефіцієнтів, які визначаються з точністю до сталого множника, то поверхня другого порядку задається не більше, ніж 9-ма точками. В деяких випадках їх кількість може бути меншою. Наприклад, сферу можна задати 4-ма точками, які їй належать. Меншою кількістю точок визначаються параболоїди.

Введемо в розгляд символи та , означивши їх рівностями

,

,

,

а також

, , .

Вираз є половиною похідної від функції по змінній , якщо змінні та при цьому вважати сталими. Аналогічно, та - це половини похідних від функції по змінних та відповідно при умові, що дві інші змінні вважаються сталими.

Найближчими нашими задачами буде дослідження властивостей поверхонь, заданих загальним рівнянням, вивчення особливостей їх розташування відносно системи координат, а також дослідження питання, скільки та які різні види поверхонь може визначати рівняння (1).

2. Перетнемо поверхню другого порядку прямою , яка проходить через деяку точку паралельно до вектора . Запишемо параметричні рівняння прямої у виді

(2)

та знайдемо точки перетину поверхні та прямої . Дістаємо систему рівнянь (1), (2), розв’язуючи яку відносно змінної , отримуємо квадратне рівняння

, (3)

де

,

, Дослідимо особливості взаємного розташування поверхні та прямої у випадках, коли деякі з коефіцієнтів рівняння (3) перетворюються в нуль.

1. Нехай . Одному із коренів рівняння , який рівний нулю, відповідає точка . Тому у цьому випадку одна із точок перетину поверхні та прямої співпадає з точкою (рис. 1).

2. Нехай та рівняння має два дійсні корені . Цим кореням відповідають дві точки, які належать заданій поверхні та прямій – це точки . У цьому випадку точка є серединою хорди (рис. 2). Якщо дане рівняння має два уявні корені, то пряма буде перетинати поверхню у двох уявних точках, а точка буде серединою уявної хорди.

3. Нехай . Рівняння має єдиний корінь , який визначає першу із точок перетину. Щоб зрозуміти особливість розташування другої точки перетину доцільно дослідити, як змінюється другий корінь рівняння (3) при . У лекції 18, де досліджувались аналогічні питання взаємного розташування лінії другого порядку та прямої, було показано, що при абсолютна величина другого кореня прямує до . Згідно із рівностями (2) при друга із точок перетину нескінченно віддаляється від точки . 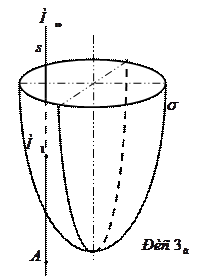Таку точку ми, аналогічно до попереднього, будемо позначати символом та говорити, що пряма перетинає поверхню у нескінченно віддаленій точці. Напрям прямої при цьому будемо називати асимптотичним. Асимптотичним буде, наприклад, напрям прямої, яка перетинає еліптичний параболоїд та проведена паралельно до його осі симетрії (рис. ), або прямої, яка проведена паралельно до твірної конуса (рис. ).

4. Випадок є поєднанням розглянутих вище випадків 1, 2. Рівняння (3) матиме вид та корені 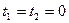. У цьому випадку пряма буде дотикатись до поверхні у точці (рис. 4).

5. При точка належить поверхні , а пряма матиме відносно асимптотичний напрям.

6. Якщо , то рівняння (3) не має розв’язків. У цьому випадку пряма не має з поверхнею спільних точок та має відносно асимптотичний напрям.

7. Якщо , то розв’язком рівняння (3) буде довільне дійсне число . Тоді кожна точка прямої належить поверхні . Ми зустрічалися із таким випадком, коли говорили про прямолінійні твірні поверхонь другого порядку, всі точки яких належать поверхні.

3. Хордою поверхні другого порядку назвемо відрізок, який сполучає дві її довільні точки.

Якщо існує точка, в якій усі хорди, які проходять через неї, діляться пополам, то цю точку називають центром поверхні.

Центр поверхні є її центром симетрії, оскільки разом із будь-якою точкою поверхні їй належить також точка, симетрична даній відносно центра.

Розглянемо питання відшукання центра поверхні, заданої рівнянням (1). Як ми знаємо, умовою того, щоб точка була серединою хорд, які проходить через неї, згідно пунктом 2), є виконання рівності

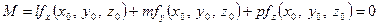
для довільного напрямку, який задається вектором . Тому для відшукання центра лінії дістаємо систему рівнянь

. (4)

Існування та кількість розв’язків системи (4) залежить від її визначника .

Якщо , то система (4) має єдиний розв’язок. У цьому випадку поверхня має єдиний центр і її називають центральною. Прикладами таких поверхонь є еліпсоїд, одно та двопорожнинний гіперболоїд, конус.

Якщо , то система (4) має безліч, або не має жодного розв’язку. Поверхню у цьому випадку називають нецентральною. Прикладами поверхонь, які не мають жодного центра, є еліптичний та гіперболічний параболоїди, параболічний циліндр. Якщо система (4) має безліч розв’язків, то в залежності від рангу її матриці відповідні розвя’зкам точки утворюють пряму або площину. Еліптичний та гіперболічний циліндри мають пряму центрів, а поверхня, яка вироджується у дві паралельні площини – площину центрів. Ця площина проходить паралельно до даних двох площин та знаходиться від них на однаковій відстані.

Приклад 1. Знайти центри поверхні, заданої рівнянням .

Розв’язання. Складемо та розв’яжемо систему рівнянь . Дістаємо , звідки . Отже, задана поверхня має єдиний центр, який знаходиться у точці .

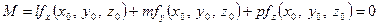4. Згідно з попереднім, пряма буде дотичною до поверхні , якщо для рівняння , яке характеризує перетин прямої з поверхнею , виконуються умови . Нехай точка належить поверхні, тобто . Всі прямі, які проходять через точку та дотикаються до поверхні, утворюють площину, оскільки незалежно від напрямку вектора вони перпендикулярні до сталого вектора . Справді, з рівності , яку можна записати у виді

,

випливає, що . Цю площину називають дотичною площиною до поверхні. Знайдемо рівняння такої площини. Оскільки відомий вектор , який перпендикулярний до площини, а також точка , яка їй належить, то рівняння дотичної площини запишеться у виді

. (5)

Нормаллю до поверхні, проведеній в деякій її точці, називають пряму, яка перпендикулярна до дотичної площини у цій же точці. Оскільки вектор паралельний до нормалі, яка проведена у точці , то рівняння останньої запишеться у виді

. (6)

Приклад 2. На поверхні знайти точки, в яких нормаль буде паралельною до осі .

Розв’язання. Оскільки вектор паралельний до осі , то . Обчислюємо .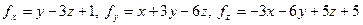

Розв’язуючи систему знаходимо шукані точки: .

Відповідь: .