Возможные (виртуальные) перемещения системы

Возможные (виртуальные) перемещения системы (ds, dj) – любая совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент наложенными на систему связями. Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинами высших порядков малости. То есть криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к их траекториям.

Число независимых между собою возможных перемещений системы называется числом степеней свободы этой системы. Например, шар на плоскости может перемещаться в любом направлении, но любое его возможное перемещение может быть получено как геометрическая сумма двух перемещений вдоль двух взаимно перпендикулярных осей. Свободное твердое тело имеет шесть степеней свободы.

Возможная (виртуальная) работа (dА) – элементарная работа, которую, действующая на материальную точку сила могла бы совершить при возможном перемещении этой точки.

Связи являются идеальными, если сумма элементарных работ реакций этих связей при любом возможном перемещении системы равна нулю, т.е. SdА^r = 0.

Принцип возможных перемещений: для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении была равна нулю:

или .

Принцип возможных перемещений дает в общей форме условия равновесия для любой механической системы, дает общий метод решения задач статики.

Если система имеет несколько степеней свободы, то уравнение принципа возможных перемещений составляют для каждого из независимого перемещений в отдельности, т.е. будет столько уравнений, сколько система имеет степеней свободы.

Общее уравнение динамики.При движении системы с идеальными связями в каждый данный момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы будет равна нулю:

.

Уравнение использует принцип возможных перемещений и принцип Даламбера и позволяет составить дифференциальные уравнения движения любой механической системы, дает общий метод решения задач динамики. Последовательность составления:

1. Приложение к каждому телу действующих на него задаваемых сил, а также условное приложение сил и моментов пар сил инерции.

2. Сообщение системе возможных перемещений.

3. Составление уравнения принципа возможных перемещений, считая систему находящейся в равновесии.

Уравнения Лагранжа 2-го рода:

, (i = 1, 2, …, s) – дифференциальные уравнения второго порядка,

где s – число степеней свободы системы (число независимых координат);

q_i – обобщенная координата (перемещение, угол, площадь и др.);

– обобщенная скорость (линейная, угловая, секторная и др.),

Т = Т (q₁, q₂,…,q_S, , , … , t) – кинетическая энергия системы;

Q_i – обобщенная сила (сила, момент и др.), ее размерность зависит от размерности обобщенной координаты и размерности работы.

Для вычисления обобщенной силы, например Q₁, необходимо задать возможное перемещение, при котором все вариации обобщенных координат, кроме dq₁, равны нулю:

dq₁ ¹ 0, dq₂ = dq₃ = dq_S = 0.

Вычисляем на этом перемещении возможную работу dА₁ всех активных сил, приложенных к системе. Имея dА₁ = Q₁dq₁, находим .

Если силы, действующие на систему, потенциальные (консервативные) (например, силы тяжести, силы упругости), то

,

где П = П (q₁, q₂, …, q_S, t) – потенциальная энергия.

Функция Лагранжа: L = T – П, тогда – уравнения Лагранжа второго рода для консервативной системы.

При стационарных связях (связях, не зависящих от времени) t не входит в выражение для кинетической энергии, тогда – квадратичная форма обобщенных скоростей, a_ij= a_ji – коэффициенты инерции. Квадратичная форма всегда положительна.

Тема 21. Малые колебания системы

Консервативная механическая система, состоящая из n материальных точек и имеющая одну степень свободы, находится в некотором положении в устойчивом равновесии. Исследуем, какое движение будет совершать эта система, если ее вывести из равновесия малым возмущением. Условимся опять определять положение системы обобщенной координатой q, выбранной так, что при равновесии q = 0. Так как равновесие устойчиво, а возмущения малы, то координата q и обобщенная скорость q́ будут во время движения оставаться величинами малыми. Для составления дифференциального уравнения движения системы воспользуемся уравнением Лагранжа, которое, если выразить обобщенную силу Q через потенциальную энергию системы П, примет вид

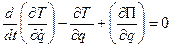. (3.1.177)

Это уравнение будет нелинейным, но его можно линеаризировать и тем самым существенно упростить, сохранив в уравнении малые величины q и только в первой степени. Для этого значения Т(q, ) и П(q) достаточно определить тоже приближенно. При этом, так как в уравнение входят первые производные от П и Т по q и , то, чтобы сохранить в нем q и в первой степени, надо Т и П определить с точностью до малых величин второго порядка малости, т.е. с точностью q² и .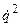

Найдем приближенное выражение Т (q, ). Для любой точки системы при стационарных связях

r_k = r_k(q);

V_k =

Тогда вынося общий множитель 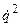за скобки, получим

или

Т =

При разложении в ряд Тейлора F(q) получим

F(q) = F(0) + (0)q + ... .

Так как Т надо определить с точностью до q², то в этом разложении следует сохранить только первое постоянное слагаемое F(0). Тогда для Т получим выражение

Т = 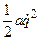, (3.1.178)

где а = F(0).

Поскольку величина Т существенно положительная, то постоянный коэффициент а > 0; его называют инерционным коэффициентом. Размерность а зависит от размерности ; в частности, а может иметь размерность массы или момента инерции.

При разложении в ряд Тейлора П(q) получим

П(q) = П(0) + , (3.1.179)

где с = .

При этом с > 0. В частном случае, если q – удлинение пружины, равенство (3.1.179) выражает потенциальную энергию поля сил упругости; поэтому коэффициент с называют обобщенным коэффициентом жесткости.

Из равенств (1.178) и (1.179) находим

Подставляя эти величины в уравнение (3.1.177), получим дифференциальное уравнение малых свободных колебаний системы с одной степенью свободы:

(3.1.180)

где k² = c/a.

Это уравнение соответствует уравнению свободных прямолинейных колебаний материальной точки и его общее решение имеет вид

q = A sin(kt +a),

где А и α – постоянные интегрирования, определяемые по начальным условиям.

Частота и период этих колебаний определяются равенствами

k = ; τ = 2π/k = 2π . (3.1.181)

Установим, как при этом движутся точки системы. Разлагая радиус-вектор одной их точек системы в ряд Тейлора и заменяя q его значением найдем, что точки системы тоже совершают малые колебания с частотой k и амплитудами . Из найденных результатов вытекают следующие свойства малых колебаний системы:

1. Свободные колебания системы являются колебаниями гармоническими; частота и период этих колебаний не зависят от начальных условий и определяются равенствами (3.1.181).

2. Так как постоянные А и α зависят от начальных условий, то амплитуды колебаний точек системы, равные , и начальная фаза тоже зависят от начальных условий.

3. Отношения амплитуд колебаний разных точек системы от начальных условий не зависят, так как определяются только значениями , т.е. конфигурацией системы;

4. Все точки системы в каждый момент времени находятся в одной и той же фазе (kt + α) и, следовательно, одновременно проходят через положения равновесия и одновременно достигают максимальных отклонений от этого положения.

При решении задач наибольший интерес представляет определение частоты k и периода τ собственных колебаний системы, что существенно, например, для установления условий наличия или отсутствия резонанса.

Тема 22. Явление удара. Ударная сила и ударный импульс

До сих пор мы изучали движение материальных точек или механических систем и, в частности, твердых тел под действием обычных сил, таких, например, как сила тяжести, сила тяготения, сила сопротивления среды и т. п., которые, непрерывно действуя на эти точки или на эти системы, имеют конечную величину. Изменение скорости точки или скоростей точек системы происходило при этом непрерывно, т. е. каждому элементарному промежутку времени соответствовало элементарное приращение скорости точки или скоростей точек систем. Например, если на падающую материальную точку действует только ее вес, то за каждый элементарный промежуток времени dt скорость точки возрастает также на элементарную величину gdt, где g – ускорение силы тяжести.

Рассмотрим движение под действием таких сил, которые действуют на материальный объект в течение весьма малого промежутка времени t, достигая очень большой величины (порядка 1/t). При этом скорости точек материального объекта резко изменяются за этот весьма малый промежуток времени, достигая конечной, а не исчезающе малой величины. Так, например, при падении тела на неподвижную плиту, как показывает опыт, за весьма малый промежуток времени, в течение которого тело соприкасается с плитой, его скорость изменяется на конечную величину.

В таких случаях следует говорить, что произошло явление удара.

С механической точки зрения, явление удара характеризуется тем, что скорости точек механической системы, а, следовательно, и количество движения этой системы за весьма малый промежуток времени, измеряемый в тысячных и меньших долях секунды, в течение которого происходит удар, изменяются на конечную величину.

Кроме приведенного выше примера, явление удара имеет место, если движущееся тело сталкивается с другим движущимся или покоящимся телом, а также, если при движении тела внезапно появляется новая связь или исчезает одна из старых. Иногда, впрочем, процесс внезапного уничтожения существующей связи называют взрывом. Явление удара также имеет место при стрельбе из орудий и при взрыве снарядов. Оно является весьма распространенным в технике, и поэтому изучение и исследование вопросов, относящихся к явлению удара, приобретает особую актуальность.

Так как при ударе конечное изменение скоростей происходит за весьма малый промежуток времени, то при этом ускорение (или замедление) получается очень большим, а, следовательно, при ударе возникают и очень большие силы. Хотя эти силы действуют на соударяющиеся тела в течение весьма малого промежутка времени, но их импульсы за этот промежуток времени являются конечными величинами.

Силы, возникающие при ударе и действующие на соударяющиеся материальные объекты в течение весьма малого промежутка времени, но достигающие при этом весьма большой величины так, что их импульсы за этот промежуток времени являются конечными величинами, называются ударными силами. Главной особенностью ударных сил является кратковременность их действия. При этом промежуток времени, в течение которого они действуют, настолько мал, что это действие оканчивается прежде, чем подверженное ему тело изменит сколько-нибудь заметно свое первоначальное положение. С другой стороны, действующие при ударе силы так велики, что за этот короткий промежуток времени действием обычных (неударных) сил можно совершенно пренебречь.

Весьма малый промежуток времени, в течение которого длится удар, называется временем удара.

Так как ударные силы очень велики и за время удара изменяются от нуля до весьма большого значения и снова падают до нуля, то в теории удара за меру механического взаимодействия соударяющихся тел принимают не сами ударные силы, а их ударные импульсы, являющиеся величинами конечными.

Ударные импульсы, появляющиеся при соударении тел и приложенные к этим телам, зависят не только от масс соударяющихся тел и их скоростей до удара, но и от упругих свойств этих тел, так что выяснить все явление удара можно, лишь применяя теорию упругости. Однако задача теории удара в теоретической механике облегчается тем, что здесь не исследуется характер деформаций, которые имеют место при ударе тел, а требуется лишь определить изменение скоростей точек системы, вызванное уже совершившимся ударом.

Тем не менее все получающиеся при этом соотношения между ударными импульсами и изменением динамических характеристик системы (количества движения, кинетического момента) используются и при изучении явления удара в конкретных задачах, так как эти соотношения остаются верными независимо от источника возникновения ударных импульсов.

Основное уравнение теории удара. Пусть данная материальная точка массой т движется под действием обычной (неударной) силы Р. Допустим теперь, что в момент t₁ когда рассматриваемая точка имеет скорость V₁, на эту точку начинает действовать ударная сила F, действие которой прекращается в момент t₂. Определим движение данной точки под действием сил Р и F за весьма короткий промежуток времени t = t₂ – t₁, в течение которого длится удар.

Применяя теорему об изменении количества движения точки, получим

,

где V₂ – скорость точки в момент t₂.

Рассмотрим отдельно каждый член правой части этого равенства.

По теореме о среднем значении определенного интеграла можно записать

; ,

где F_cp и Р_ср – значения сил F и Р в некоторый определенный момент t внутри участка интеграции.

При этом Р_ср является конечной величиной; ударная же сила F за время удара t = t₂ – t₁ достигает весьма большой величины F_cp (порядка 1/t). Поэтому произведение P_срt будет пренебрежимо мало по сравнению с произведением F_cpt, являющимся величиной конечной. Из этих рассуждений следует, что импульс S_неуд обычной (неударной) силы Р за время удара t будет по сравнению с импульсом S_уд ударной силы F очень мал и им можно пренебречь. В результате окончательно находим

. (3.1.182)

Будем в дальнейшем обозначать скорость точки в начале удара через v, а скорость этой же точки в конце удара – через и. Тогда уравнение (1.182) можно записать в виде

. (3.1.183)

Это уравнение представляет выражение теоремы об изменении количества движения точки при ударе, которая может быть сформулирована так: изменение количества движения материальной точки за время удара равно действующему на эту точку ударному импульсу.

Если на точку одновременно действуют несколько ударных импульсов, то изменение количества движения точки равно геометрической сумме этих ударных импульсов.

Проектируя векторное равенство (3.1.183) на координатные оси, получим три следующих равносильных ему скалярных уравнения:

ти_x – mv_x = S_x;

ти_у – mv_y = S_y;

mu_z – mv_z = S_z.

Таким образом, изменение проекции количества движения материальной точки на какую-нибудь неподвижную ось за время удара равно проекции на ту же ось действующего на эту точку ударного импульса.

Уравнение (3.1.183) является основным уравнением теории удара и играет такую же роль, как второй закон динамики при изучении движений под действием обычных сил.

Выясним теперь, как перемещается материальная точка за время удара.

Так как

и = dr/dt,

где r – радиус-вектор, определяющий положение данной точки относительно некоторой системы отсчета,

то уравнение (1.183) можно записать следующим образом:

.

Проинтегрировав это равенство в пределах от t₁ до t₂, найдем

,

где S_ср – есть среднее значение ударного импульса за время удара t = t₂ – t₁.

Учитывая при этом, что v и S_cp – величины конечные, а t весьма мало, приходим к выводу, что будет близко к нулю и, следовательно, за время удара перемещение точки практически равно нулю.

Таким образом, перемещением материальной точки за время удара можно пренебречь, считая, что за время удара эта точка практически остается неподвижной, т.е. не успевает переместиться.

В заключение отметим, что основное уравнение удара (1.183) является не дифференциальным уравнением, а уравнением с конечными величинами, из которого можно определить изменение скорости точки за время удара, если задан ударный импульс, или определить ударный импульс, если заданы скорости в конце удара и в начале удара.

Подобно этому, все другие уравнения теории удара, с которыми мы встретимся ниже, будут алгебраическими (конечными), а не дифференциальными уравнениями.

Теорема об изменении кинетического момента системы при ударе. Если обозначим кинетический момент системы относительно центра О в начале удара через , а в конце удара – через , то будем иметь

. (3.1.184)

Уравнение (3.1.184) представляет выражение теоремы об изменении кинетического момента при ударе и может быть сформулировано так: изменение за время удара кинетического момента системы относительно какого-нибудь неподвижного центра равно геометрической сумме моментов всех внешних ударных импульсов, действующих на эту систему относительно того же центра.

Если , то .

Отсюда следует, что внутренние ударные импульсы не могут изменить кинетического момента всей системы.

Проектируя векторы обеих частей уравнения (1.184) на координатные оси, получим

;

;

.

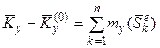Таким образом, изменение за время удара кинетического момента системы относительно какой-нибудь неподвижной оси равно сумме моментов всех внешних ударных импульсов, действующих на эту систему относительно той же оси.

Контрольные вопросы

1. Сформулируйте основные законы механики.

2. Две основные задачи динамики. Кратко изложите схему решения.

3. Сформулируйте принцип Даламбера для материальной точки и запишите его уравнение.

4. Что называют даламберовой силой инерции материальной точки? Куда фактически приложена эта сила?

5. Дифференциальные уравнения относительного движения материальной точки.

6. Что такое переносная и кориолисова силы инерции? Как определяются их абсолютные величины и направления?

7. Принцип относительности классической механики. Сформулируйте условие относительного покоя материальной точки и сравните его с условием абсолютного покоя. Чем отличаются состояния равновесия материальной точки в инерциальной и неинерциальной системах отсчета?

8. Что называют механической системой? Связи. Классификация сил.

9. Чему равна масса механической системы? Как определяются координаты ее центра масс?

10. Дайте определения момента инерции твердого тела относительно центра, плоскости и оси.

11. Теорема о моменте инерции тела относительно параллельных осей. Относительно какой оси момент инерции тела минимален?

12. Запишите формулы, по которым вычисляются осевые моменты инерции простейших тел.

13. Теорема о движении центра масс системы. В каких случаях движение центра масс системы не изменяется? Приведите пример.

14. Теоремы об изменении количества движения точки и механической системы.

15. Закон сохранения количества движения системы. Приведите примеры.

16. Динамика точки переменной массы.

17. Теорема о моменте количества движения точки.

18. Теорема о кинетическом моменте системы.

19. Кинетический момент вращающегося твердого тела относительно оси вращения.

20. Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

21. Принцип Даламбера для механической системы.

22. Вычисление сил инерции в различных случаях движения твердого тела.

23. Теорема об изменении кинетической энергии материальной точки и системы.

24. Кинетическая энергия твердого тела в различных случаях движения.

25. Работа силы тяжести и упругой силы.

26. Работа и мощность силы, приложенной к вращающемуся твердому телу.

27. Работа силы на прямолинейном участке пути и работа пары трения качения.

28. Мощность силы и коэффициент полезного действия.

29. Что такое потенциальная энергия материальной точки. Что она характеризует и как вычисляется?

30. Рассмотрите задачи о движении физического маятника. От чего зависит период его колебаний?

31. Что такое гироскопы, как они устроены и где применяются?

32. Какими свойствами обладает свободный гироскоп?

33. Возможные перемещения системы. Число степеней свободы. Принцип возможных перемещений.

34. Общее уравнение динамики.

35. Теория удара.

36. Обобщенные координаты.

37. Уравнение Лагранжа 2-го рода.