Сопротивление материалов. Тема 1. Центральное растяжение – сжатие

Тема 1. Центральное растяжение – сжатие

Основные понятия, допущения и гипотезы. В статике изучаются абсолютно твердые тела, которые под действием внешних сил не изменяют размеров и формы. В действительности таких тел нет, все реальные элементы конструкций и машин при действии на них внешних сил изменяют свою форму и размеры – деформируются и при некоторой величине сил могут разрушиться.

Способность деформироваться – одно из основных свойств всех твердых тел. Она является следствием их молекулярного строения. Как известно, твердые тела состоят из молекул, расположенных беспорядочно (аморфное строение) или в определенном порядке (кристаллическое строение). Молекулы не заполняют всего объема тела, а удерживаются на некотором расстоянии одна от другой под влиянием межмолекулярных сил взаимодействия. Приложение внешних сил нарушает нормальные расстояния между молекулами, и тело деформируется. При этом изменяется нормальное межмолекулярное взаимодействие и внутри тела возникают силы, которые противодействуют деформации и стремятся вернуть частицы тела в прежнее положение. Эти внутренние силы называют силами упругости, а свойство тел устранять деформацию после прекращения действия внешних сил называется упругостью.

Если тело не восстанавливает первоначальной формы и размеров, деформации называют остаточными, или пластичными. Наличие остаточных деформаций в деталях машин в подавляющем большинстве недопустимо. Внутренние силы могут увеличиваться лишь до определенного предела, характеризуемого прочностью материала. Если внутренние силы не в состоянии уравновесить внешние нагрузки, тело разрушается.

Для расчета реальной конструкции, установления математических соотношений между действующими силами, геометрическими размерами деталей конструкции, деформациями и силами упругости необходимо отбросить несущественные, с точки зрения расчета, факторы, т.е. идеализировать конструкцию – создать расчетную схему, сохраняющую основные свойства реальной конструкции, но лишенную ее второстепенных свойств.

Основные допущения и принципы, принятые при расчете конструкций:

1. Все тела предполагаются абсолютно упругими.

2. Все тела по своему строению предполагаются сплошными, не имеющими во внутренней структуре трещин или полостей.

3. Материал рассматривается как однородная, изотропная, сплошная среда, обладающая свойством упругости.

Изотропный материал обладает одинаковыми физико-механическими свойствами во всех направлениях (не изотропный материал – дерево, оно по-разному сопротивляется нагружению вдоль и поперек волокон).

4. Перемещения точек тела под действием нагрузок очень малы по сравнению с размерами тела, поэтому уравнения равновесия составляются как для недеформируемого тела.

5. Перемещения точек упругого тела прямо пропорциональны действующим нагрузкам.

6. Внешние силы действуют независимо друг от друга. Результат действия на тело нескольких сил равен сумме результатов действия каждой силы, при этом порядок приложения сил безразличен. Это положение известно под названием принципа независимости действия сил.

Классификация сил.Внешние силы– это активно приложенные нагрузки – силы и моменты. Например, усилие пилота на рычаге, вращающий момент, действующий на вал со стороны привода, сила тяги ВС – типичные приложенные нагрузки. Приложенная нагрузка может создаваться в результате активного воздействия на тело окружающей среды (температурная нагрузка на лопатки турбины со стороны потока раскаленных газов, аэродинамическая нагрузка на крыло от встречного воздушного потока и др.). К внешним нагрузкам относят также реакции. Эти нагрузки прикладываются к нагруженным элементам со стороны сопрягающихся с ними опор, например, сила противодействия пилоту со стороны рычага, нагрузка на вал со стороны подшипников, силы и моменты со стороны фюзеляжа на крыло или стойку шасси и т.д.

Внешние нагрузки, прикладываемые к авиаконструкциям в процессе эксплуатации техники, могут достигать сотен тонн, действовать кратковременно или длительно.

По характеру действия силовые факторы подразделяются на статические и динамические нагрузки.

Статические нагрузки – силы и моменты, постоянные или медленно изменяющиеся по величине (детали и узлы ВС на стоянке или при установившемся горизонтальном полете. Пилот медленно и плавно нажимая на рычаг управления, прикладывает к нему статическую нагрузку).

Динамические нагрузки – силы и моменты, которые прикладываются внезапно, сразу полной своей величиной (ударные), быстро нарастающие либо убывающие (инерционные), изменяющиеся по направлению (циклические). Например, на шасси самолета в момент приземления действует со стороны грунта динамическая нагрузка ударного характера; изменение скорости полета сопровождается возникновением инерционных нагрузок на детали и узлы самолета и двигателя; под циклической нагрузкой можно рассматривать комплекс усилий, вызывающий вибрацию крыла.

По способу приложения силовые факторы подразделяются на сосредоточенные и распределенные.

Сосредоточенными силами называются силы, передающиеся на элемент конструкции через площадку, размеры которой очень малы по сравнению с размерами всего элемента. Например, силы, действующие на узлы крепления двигателя к самолету, на узлы крепления элеронов, рулей и т.д.

Распределенными силами называют силы, приложенные к элементам конструкции на протяжении некоторой длины или площади, и которые могут быть равномерно распределенными или неравномерно распределенными. Так аэродинамическая нагрузка по поверхности крыла представляет собой нагрузку, неравномерно распределенную по площади.

Вес горизонтально расположенной балки представляет собой нагрузку, равномерно распределенную по длине (погонную нагрузку).

Для полки лонжерона крыла, сечение которой уменьшается от корневой части к консоли, нагрузка от собственного веса является неравномерно распределенной по длине.

Метод сечений. Виды деформаций. Напряжения. Будем рассматривать внутренние силы и деформации, возникающие в элементах конструкций, схематизированных в форме бруса (вал двигателя, тяга управления, лонжерон), длина которых значительно превышает их поперечные размеры. Брус может быть прямым (валы, оси, тяги, балки) или кривым (крюк, пружина, звено цепи), иметь постоянное или переменное сечение. Например, подкос шасси самолета считают брусом постоянного сечения, лопатку компрессора ГТД, лопасть воздушного винта – брусом переменного сечения. Кроме стержней (брусьев), могут встречаться пластинки или оболочки, у которых только один размер (толщина) мал по сравнению с двумя другими, и массивные тела, у которых все три размера примерно одинаковы.

Выше отмечалось, что внешние силы, действующие на тело, вызывают в нем внутренние силы упругости. Эти внутренние силы стремятся уничтожить полученную телом деформацию. Обнаружить возникающие в нагруженном теле внутренние силы можно, применив метод сечений. Суть метода заключается в том, что внешние силы, приложенные к отсеченной части тела, уравновешиваются внутренними силами, возникающими в плоскости сечения – заменяющими действие отброшенной части тела на оставленную.

Рассечем находящийся в равновесии стержень на две части (рис. 3.2.1, а). В сечении возникают внутренние силы упругости (рис. 3.2.1, б), уравновешивающие внешние силы, приложенные к отсеченной части. Это позволяет применить к любой отсеченной части тела условия равновесия, дающие в общем случае пространственной системы сил шесть уравнений. В соответствии с правилами статики, приведем внутренние силы к главному вектору и главному моменту. Разложим главный вектор и главный момент внутренних сил на составляющие по осям координат (рис. 3.2.2): – продольная сила; и – поперечные силы (срезающие или сдвигающие); 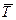– крутящий момент; M_x и M_y – изгибающие моменты.

Рис. 3.2.1

В частных случаях отдельные силовые факторы могут быть равны нулю. Координатные оси будем направлять следующим образом: ось Z – вдоль оси стержня, а оси X и Y – вдоль главных центральных осей его поперечного сечения.

Внутренние силовые факторы, возникающие в поперечном сечении стержня, полностью определяют характер его деформации. Деформации отдельных элементов могут быть сложными, но любую деформацию всегда можно представить как сочетание нескольких простейших деформаций.

Известны следующие простейшие виды деформаций стержней:

- осевое растяжение и сжатие – такой вид деформации, при котором в любом поперечном сечении стержня возникает только продольная сила (работа тросов, канатов, цепей, тяг управления ВС, стоек шасси, подкосов рамы двигателя, шатунов поршневых двигателей);

- сдвиг или срез – такой вид деформации, при котором в любом поперечном сечении бруса возникает только поперечная сила (работа болтов подвижных соединений, цапф, пальцев сочленения, сварных швов, шпонок и др.);

- кручение – такой вид деформации, при котором в любом поперечном сечении бруса возникает только крутящий момент (работа валов, крыла и фюзеляжа ВС, рулей и элеронов, работа стойки шасси);

- изгиб чистый – такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент.

Если в сечении стержня возникает еще и поперечная сила, то изгиб называют поперечным (работа всякого рода балок, лонжеронов крыла, качалок управления ВС, ручки управления ВС, стойки шасси).

Напряжения. Принято считать, что внутренние силы действуют непрерывно по всему сечению. Мерой их интенсивности является напряжение – величина внутренних сил, приходящихся на единицу площади сечения (рис. 3.2.3). Напряжение представляет собой отношение внутренней силы к некоторой площади и измеряется в единицах силы, отнесенных к единице площади (1 H/м² = 1 Па). В практических расчетах удобно измерять напряжения в мегапаскалях (1 МПа = 1 Н/мм² = 10⁶ Па = 10⁶ Н/м²).

Рис. 3.2.3

Через одну и ту же точку тела можно провести бесчисленное множество сечений, разделяющих тело на две части. В общем случае напряжения по различным сечениям будут различны.

Напряжения в некоторой точке какого-либо сечения тела характеризуются числовым значением и направлением, т.е. напряжение представляет собой вектор, наклоненный под тем или иным углом к рассматриваемому сечению. Направление и числовая величина напряжения зависят от характера и величины внешних сил, приложенных к телу, от положения сечения в теле и положения точки в сечении.

Пусть в некоторой точке k сечения тела по некоторой малой площадке DА действует сила под некоторым углом к площадке (см. рис. 3.2.3).

Поделив эту силу на площадь ΔА, найдем возникающее в точке k напряжение:

при DА® 0. (3.2.1)

Разложим напряжение на составляющие: (сигма) – нормальное напряжение (по нормали к площадке ΔА) и 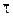(тау) – касательное напряжение.

Полное напряжение и его составляющие являются векторами. Рассматривая нормальное или касательное напряжения по какому-либо сечению, мы тем самым точно фиксируем их направление. Поэтому эти напряжения не принято обозначать, как векторы. Нормальное напряжение возникает при сближении или отрыве частиц тела, а касательное – при скольжении или сдвиге частиц.

При решении задач сопротивления материалов удобнее оперировать не с полным напряжением, а с его составляющими, среднюю величину которых при равномерном распределении нагрузки можно вычислить по формулам:

σ = ; t = . (3.2.2)

Полное напряжение определяется по формуле

. (3.2.3)

Напряжение, при котором происходит разрушение материала или возникают заметные пластические деформации, называют предельным, и обозначаются σ_пр, τ_пр. Эти напряжения определяют опытным путем.

Во избежание разрушения элементов сооружений или машин, возникающие в них рабочие (расчетные) напряжения (σ, τ) не должны превышать так называемые допускаемые напряжения – наибольшие напряжения, при которых обеспечивается надежная работа детали.

Допускаемые напряжения обозначаются буквами в квадратных скобках: [σ], [τ] и вычисляются по формулам:

[σ ] = σ_пр/[n], [τ ] = τ_пр/[n], (3.2.4)

где [n] = 1,2, … 5 – коэффициент запаса прочности.

Выбор допускаемых напряжений и запаса прочности детали производится с учетом характера действия нагрузок, механических свойств материала, назначения проектируемой конструкции, вида деформации детали, наличия или отсутствия концентрации напряжений, точности расчета и других факторов. Назначение недостаточного запаса может привести к разрушению детали, излишне большой запас приводит к перерасходу материала и утяжелению конструкции.

Опасным напряжением для пластичного материала будет предел текучести σ_т, по которому и берется допускаемое напряжение, опасным же напряжением для хрупкого материала будет предел прочности σ_в, тогда

[σ] = σ_т/[n] и [σ ] = σ_в/[n]. (3.2.4¢)

Нагрузка, по которой следует производить расчет на прочность, должна быть больше эксплуатационной, чтобы обеспечить безопасность работы конструкции для этого вводится коэффициент безопасности (f) – число, показывающее во сколько раз разрушающая нагрузка F_р будет больше эксплуатационной. Коэффициент безопасности определятся по формуле

.

Растяжение и сжатие. Эпюры продольных сил и нормальных напряжений. Растяжением или сжатием называется такой вид нагружения, при котором в поперечных сечениях бруса возникает только продольная сила (N), действующая перпендикулярно плоскости поперечного сечения.

Многие детали и узлы авиатехники в процессе эксплуатации испытывают деформацию растяжения или сжатия. Болты и шпильки при затяжке растягиваются. Тяги управления ВС и двигателем, в зависимости от характера и режима полета, растягиваются или сжимаются. Растяжение и сжатие воспринимают полки лонжеронов, шатуны кривошипных механизмов, рама крепления двигателя к самолету, стойки шасси и т.д.

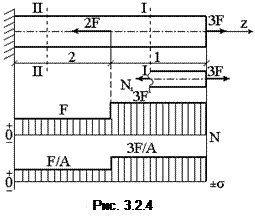
Рассмотрим невесомый, защемленный левым концом прямой брус, вдоль оси которого действуют силы 2F и 3F (рис. 3.2.4).

1. Разбиваем брус на участки, границами которого являются точки приложения сосредоточенных сил или изменение поперечного сечения.

2. Методом сечений на каждом участке определяем продольные силы N₁ и N₂, начиная со свободного конца. Во всех точках поперечного сечения бруса будут действовать внутренние распределенные силы, равнодействующая которых определится из условия равновесия одной из частей бруса.

ΣZ = – N₁ + 3F = 0; N₁ = 3F.

Аналогично находим продольную силу N₂:

ΣZ = – N₂ – 2F + 3F = 0; N₂ = F.

В пределах одного участка продольная сила будет иметь постоянное значение. Растягивающие продольные силы будем считать положительными, а сжимающие – отрицательными.

3. Нормальные напряжения равномерно распределенные по сечению определяются по формуле

σ = 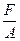. (3.2.5)

Для наглядного изображения распределения вдоль оси бруса продольных сил и нормальных напряжений строят графики, называемые эпюрами, причем для нормальных напряжений применяется тоже правило знаков, что и для продольных сил (см. рис. 3.2.4).

Условие прочности при растяжении – сжатии:

s_max = 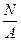< [σ ]. (3.2.6)

Три задачи, решаемые из условия прочности:

1. Определение безопасной нагрузки, если известны размеры и материал:

F =N < A [σ].

2. Проектный расчет – определение размеров поперечного сечения, если известна нагрузка и материал:

A > .

3. Проверка прочности:

σ_max < [σ].

Деформации при растяжении, сжатии. Закон Гука. Английский ученый Роберт Гук (1635–1703) установил зависимость между напряжением и деформацией, которое формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.

Математически закон можно записать в виде равенства

σ = E ε. (3.2.7)

Коэффициент пропорциональности E характеризует жесткость материала, т.е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода (табл.).