Эпюры крутящих моментов.Для наглядного изображения распределения крутящих моментов вдоль оси бруса строят эпюры крутящих моментов.

Для определения крутящего момента в сечении используют метод сечений. Рассмотрим пример на рис. 3.2.16. Вращающий момент подводится к валу (брус круглого сечения) от шкива 1 и снимается с вала через передающие шкивы 2, 3, 4 на другие валы механизма. Для определения крутящего момента в сечении х = х₁, рассмотрим равновесие, например, левой части от сечения. Составим уравнение равновесия:

; ,

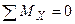откуда Т_кр = М₁.

Рис. 3.2.16

При рассмотрении равновесия правой части получим

В любом сечении вала действует крутящий момент, равный сумме крутящих моментов, лежащих по одну сторону от этого сечения.

Диаграмму (рис. 3.2.16), показывающую распределение значений крутящих моментов по длине вала, называют эпюрой крутящих моментов. Для построения таких эпюр следует придерживаться правила знаков. Принято считать, что если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит результирующий момент внешних пар, приложенных к рассматриваемой части вала, вращающим ее в направлении против хода часовой стрелки, то крутящий момент считается положительным, а вращающий момент внешних сил – отрицательным. При противоположном направлении – наоборот. Эпюра крутящих моментов вала показывает степень нагруженности участков вала.

При расчете валов на прочность часто задается не вращающий момент, а мощность, передаваемая валом, и частота вращения вала. Тогда вращающий момент определяют по формуле

М = 9554 (Н×м),

где M – вращающий момент, Н×м;

P – можность, передаваемая валом, кВт;

n – частота вращения вала, об/мин.

Пример. Проверьте на прочность вал редуктора поршневого двигателя, если наружный диаметр (D) равен 92 мм, внутренний диаметр (d) равен 60 мм, допускаемое напряжение для материала вала [τ ] = 35 МПа. Двигатель развивает мощность (P), равную 1050 л. с. при оборотах вала редуктора n = 1800 об/мин. 1 л. с. = 0,736 кВт.

Решение. Найдем полярный момент сопротивления и крутящий момент сечения:

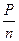W_r = = 125×10³ мм³; Т_кр = 9554 = 4180 Hм;

t_max = 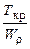= = 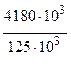33,5 MПа < 35 МПа.

Максимальное касательное напряжение меньше допускаемого напряжения для материала вала, следовательно, условие прочности выполняется.

Тема 6. Изгиб

Изгибом называется такой вид деформации, когда под действием внешних сил в поперечных сечениях бруса возникают изгибающие моменты. Брусья, работающие на изгиб, называют балками. На изгиб работают валы, оси и другие детали конструкций.

Различают два основных вида изгиба: чистый и поперечный. Если применить метод сечений в случае чистого изгиба (рис. 3.2.17, а), то отрезанная часть балки уравновешивается только моментом, а в случае поперечного изгиба (рис. 3.2.17, б) – моментом и поперечной силой.

По центру тяжести проходит нейтральный слой, не испытывающий ни растяжения, ни сжатия. Растяжение волокон сопровождается их утонением, а сжатие – утолщением. Выясним, как распределяются напряжения по сечению. По закону Гука s = E×e.

Из рис. 3.2.18 видно, что абсолютное удлинение волокон рассматриваемого слоя равно

а относительное удлинение

.

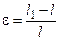Если точка О – общий центр кривизны деформированных слоев, то

и ,

где r – радиус кривизны нейтрального слоя;

dj – центральный угол;

у – расстояние от нейтрального до рассматриваемого растянутого слоя.

Рис. 3.2.18

Следовательно,

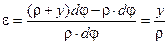и .

Таким образом, напряжения в сечении пропорциональны расстоянию у от нейтрального слоя и изменяются по линейному закону. Наибольшее напряжение испытывают волокна периферийного слоя при y = y_max:

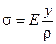, (3.2.22)

где s – напряжение в произвольной точке поперечного сечения при изгибе.

Чтобы выяснить зависимость напряжений от действующих в сечении изгибающих моментов, выделим в сечении А элементарную площадку DА (риc. 3.2.18, б), расположенную на расстоянии у от нейтрального слоя. Элементарная сила sdA создает момент sdAy. Cуммируя элементарные моменты в сечении и учитывая (3.2.22), получим полный момент по всей площади сечения:

M = sydA = .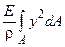

Введем геометрическую характеристику сечения – осевой момент инерции поперечного сечения ( )

Тогда

,

отсюда

,

из формулы (2.22)

,

т.е.

или .

Напряжение будет максимальным, если у = у_max:

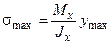. (3.2.23)

Введем еще одну геометрическую характеристику сечения – осевой момент сопротивления ( 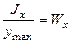), характеризующий степень сопротивляемости поперечного сечения изгибу относительно нейтральной оси.

Окончательно получаем

s_max = . (3.2.24)

Известно, что условие прочности выражается следующим образом:

. (3.2.24¢)

Из этого условия прочности вытекают три задачи, решаемые при плоском изгибе:

Проектный расчет, т.е. определение необходимых размеров поперечного сечения:

.

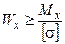Для круглого сечения диаметром d

W_x = 0,1d³; (3.2.25)

для кольцевого сечения:

W_х = 0,1(d_н⁴ – d_в⁴)/d_н, (3.2.25¢)

для прямоугольного сечения:

W_x = bh²/6, (3.2.26)

где b – ширина бруса;

h – высота бруса.

Из последней формулы видно, что прочность бруса на изгиб зависит не только от формы поперечного сечения, но и от его положения, вертикальное положение прямоугольного сечения более выгодно, чем горизонтальное (попробуйте согнуть школьную линейку, расположенную плашмя, а затем ребром).

Поскольку на изгиб работают главным образом периферийные слои, целесообразно применять брусья с сечениями, в которых работающий материал расположен дальше от нейтральной оси. Так, применение кольцевого сечения (трубы) целесообразнее применения сплошного, прямоугольного выгоднее квадратного, причем, чем больше отношение h/b, тем лучше. Но наиболее выгодными являются специальные профили: двутавр и швеллер, которые и имеют наибольшее применение и в строительстве и в машиностроении. Моменты сопротивления этих профилей приводятся в справочниках.

Опоры и опорные реакции балок. Балки служат для передачи действующих на них нагрузок на опоры, на которых они покоятся. На опорах балки возникают реакции, с определения которых следует начинать решение всех задач, связанных с изгибом балок. В зависимости от числа и устройства опор балки число реакций, подлежащих определению, бывает различно. Опоры балок по их устройству могут быть разделены на следующие три основных типа: шарнирно-неподвижная опора; шарнирно-подвижная опора; жестко-защемленная опора.

Шарнирно-неподвижная опора показана на рис. 3.2.19, а. Конец балки 3 опирается на шарнир 1. Шарнир 1 лежит на опорной подушке 2, которая, в свою очередь, жестко прикреплена к опорной плоскости. Такая опора не дает концу балки возможности передвигаться в каком-либо направлении, позволяя ему только поворачиваться относительно центра шарнира. В дальнейшем шарнирно-неподвижную опору будем изображать схематически, как показано на рис. 3.2.19, б.

Относительно реакции, возникающей в шарнирно-неподвижной опоре, нам известно только, что она лежит в плоскости действия нагружающих балку сил и проходит через центр шарнира. Величина и направление реакции нам неизвестны. Неизвестную по величине и направлению реакцию всегда можно заменить двумя ее составляющими – одной вертикальной и другой горизонтальной (рис. 3.2.19, в).

Шарнирно-подвижная опора показана на рис. 3.2.20, а. Такая опора отличается от шарнирно-неподвижной тем, что у нее опорная подушка поставлена на катки, дающие ей возможность передвигаться вместе с концом балки вдоль ее оси по опорной плоскости. В дальнейшем шарнирно-подвижную опору будем изображать схематически, как показано на рис. 3.2.20, б.

Шарнирно-подвижная опора налагает на конец балки только одну связь – она не дает концу балки перемещаться в направлении, перпендикулярном к оси балки. Следовательно, шарнирно-подвижная опора дает лишь одну реакцию, неизвестную по величине, но известную по направлению.

Жесткое закрепление конца балки показано схематически на рис. 3.2.21. Такая опора препятствует всякому перемещению конца балки в плоскости действия внешних нагрузок и, кроме того, препятствует вращению конца балки. В жестком защемлении возникает реакция, неизвестная по величине и направлению, препятствующая перемещению конца балки, и реактивный момент, препятствующий повороту конца балки. Неизвестную реакцию всегда можно заменить двумя составляющими – одной вертикальной 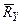, и другой горизонтальной . На этом основании можно сказать, что на опоре, представляющей жесткое защемление, возникают три неизвестные реакции: вертикальная реакция , горизонтальная реакция и опорный момент М.

Рис. 3.2.21

Определение опорных реакций балок.При всех видах деформаций, изучаемых в сопротивлении материалов, предполагается, что величины деформации невелики, поэтому при определении опорных реакций балок можно пренебречь теми изменениями, которые происходят в расположении внешних сил, действующих на балку вследствие деформации балки. В случае действия на балку сил, лежащих в одной плоскости, статика дает три уравнения равновесия:

Σ X_i =0, Σ Y_i =0, Σ М_i = 0,

т.е. для равновесия балки необходимо, чтобы суммы проекций всех сил, приложенных к балке, вместе с реакциями опор на оси х и у были равны нулю; кроме того, должна быть равна нулю и сумма моментов всех сил относительно любой точки плоскости.

Если силы, изгибающие балку, перпендикулярны ее оси, то уравнение Σ X_i = 0 обращается в тождество, и для определения реакций остаются два уравнения статики:

1) ∑Y_i =0; 2) Σ М_i = 0.

Если балка при поперечном изгибе имеет такие опоры, что общее число реакций, возникающих на опорах, не превышает двух, то реакции могут быть всегда определены из двух уравнений статики. Такие балки, реакции которых могут быть определены из уравнений статики, называются статически определимыми балками.

Статически определимые балки могут быть только следующих двух видов:

1) балка с одним жестко-защемленным и другим свободным концом, иначе консоль (рис. 3.2.22, а);

2) балка с одной шарнирно-неподвижной и другой шарнирно-подвижной опорами (рис. 3.2.22, б, в).

Рис. 3.2.22

Рассмотрим на конкретном примере определение реакций статически определимых балок.

Предварительно условимся ось Х направлять всегда по оси балки, ось Y – вертикально вверх. При составлении уравнений моментов за положительные моменты условимся считать моменты, направленные против часовой стрелки. Если на балку действует сплошная равномерно распределенная нагрузка, как показано на рис. 3.2.23, то при определении реакций сплошная нагрузка заменяется ее равнодействующей. Точка приложения равнодействующей сплошной распределенной нагрузки лежит посередине того участка, на который она действует. Сплошная равномерно распределенная нагрузка часто задается ее интенсивностью.

Под интенсивностью распределенной нагрузки понимают величину нагрузки, приходящуюся на единицу длины. Если вся сплошная нагрузка равна F, а длина участка, на который она действует l, то интенсивность нагрузки будет определяться по формуле

q = .

Размерность интенсивности нагрузки выражается обычно в Н/м или Н/мм.

Пример. Балка, защемленная одним концом (СМ. рис. 3.2.23), нагружена равномерно-распределенной нагрузкой интенсивности 0,5 кН/м по всей длине балки и сосредоточенной силой, равной 2кН, на свободном конце. Определите реакции защемления, если длина балки равна 4 м.

Решение. В защемлении возникают вертикальная реакция и реактивный момент. Направление этих реакций нам неизвестно. Направим пока произвольно вертикальную реакцию (R) вверх, а опорный момент М против вращения часовой стрелки. Напишем условия равновесия, выбрав за центр моментов точку А:

åM_A = M – – Fl = 0,

откуда находим величину реактивного момента:

M = .

Из уравнения проекций сил на ось Y получаем:

åU_i = R – ql – F = 0,

откуда находим реакцию защемления:

R = ql + F = 0,5 ×4 + 2 = 4 кH.

В данном случае момент М и реакция R получились положительными. Это указывает на то, что их направления нами были выбраны правильно. Если после определения реакций какая-либо из величин получается со знаком минус, то это показывает, что предварительно выбранное ее направление не совпадает с действительным. Поэтому в этом случае направление реакции, полученной со знаком минус, следует изменить на чертеже на противоположное и в дальнейших расчетах учитывать ее действительное направление.

Построение эпюр изгибающих моментов и поперечных сил. Для оценки прочностной надежности балки следует установить сечения, в которых внутренние силовые факторы (поперечная сила (Q) и изгибающий момент (М)) имеют максимальные значения. Анализ внутренних силовых факторов будет наглядным, если построить графики изменения поперечных сил и изгибающих моментов вдоль центральной оси балки. Эпюры строятся аналогично эпюрам продольных сил и крутящих моментов. При построении эпюр положительные значения поперечных сил и моментов откладывают вверх от оси, отрицательные – вниз; ось эпюры проводят параллельно оси балки.

Рассмотрим простую балку, нагруженную двумя силами F₁ и F₂ (рис. 3.2.24). Пусть реакции на левой и правой опорах будут равны R_A и R_B. Для определения внутренних сил упругости в каком-либо сечении балки применим метод сечений. Разрежем мысленно балку в сечении, отстоящем на расстоянии х от левой опоры балки, и рассмотрим левую часть балки, отбросив ее правую часть.

Рис. 3.2.24

Для того чтобы левая часть балки находилась в равновесии, в сечении должны действовать поперечная сила Q и изгибающий момент М. Из условия равновесия левой части балки имеем

, R_A – F₁ – Q = 0, откуда Q = R_A – F₁;

, R_Ax – F₁(x – a) – M = 0, откуда М = R_A · x – F₁(x – a).

Сила Q – результирующая внутренних сил, приложенная к оставшейся части балки, численно равная алгебраической сумме внешних сил, действующих по одну сторону от сечения, называется поперечной или перерезывающей силой.

Момент пары внутренних сил, приложенный к оставшейся части балки, численно равный алгебраической сумме моментов внешних сил, действующих по одну сторону от сечения, называется изгибающим моментом в сечении.

Так как вся балка под действием внешних сил вместе с силами реакций находится в равновесии, то сумма всех сил, действующих на часть балки, лежащую левее сечения, должна быть равна сумме всех сил, действующих на часть балки, лежащую правее сечения, но иметь обратное направление.

По тому же условию равновесия момент равнодействующей пары всех сил, действующих левее сечения относительно центра тяжести сечения, должен быть равен моменту равнодействующей пары сил, действующих правее сечения относительно центра тяжести сечения, но иметь обратное направление.

Правило знаков при построении эпюр поперечных сил и изгибающих моментов:изгибающий момент положительный, если он изгибает балку выпуклостью вниз и изгибающий момент отрицательный, если он изгибает балку выпуклостью вверх (рис. 3.2.25, а).

Поперечная сила положительная, если равнодействующая внешних сил слева от сечения направлена вверх, а справа от сечения – вниз и наоборот (рис. 3.2.25, б).

Примеры построения эпюр.Рассмотрим ряд типовых примеров, содержащих наиболее часто встречающиеся случаи нагружения.

Пример 1. При построении эпюр для балок с одним защемленным концом можно не определять опорных реакций. Проведя сечение, будем рассматривать равновесие той части, к которой приложены только внешние активные силы. Для балки (рис. 3.2.26, а) такой частью будет левая. В произвольном сечении балки на расстоянии х = 0 от свободного конца поперечная сила равна нулю (Q = 0), так как внешняя нагрузка не дает составляющей перпендикулярной оси балки.

Изгибающий момент в любом сечении равен внешнему моменту на свободном конце; он положителен, так как балка от действия внешнего момента получает положительную кривизну. Эпюры поперечных сил и изгибающих моментов построены на рис. 3.2.26, б, в. Балка в рассмотренном примере испытывает чистый изгиб, так как поперечная сила во всех ее поперечных сечениях равна нулю. Эпюра моментов при чистом изгибе представляет собой прямую линию, параллельную оси балки.

Пример 2. Построим эпюры для балки с защемленным концом, нагруженной сосредоточенной силой на свободном конце (рис. 3.2.27, а). Здесь можно не определять опорных реакций. Проведя сечение, будем рассматривать равновесие правой части, к которой приложены внешние активные силы. В любом сечении балки на расстоянии х от свободного конца поперечная сила равна силе F и положительна, так как внешняя сила стремится опустить правую часть балки (Q = F). Эпюра поперечных сил (рис. 3.2.27, б) представляет собой прямую линию, параллельную оси балки.

Изгибающий момент в произвольном поперечном сечении балки на расстоянии х от свободного конца равен моменту внешней силы F относительно центра этого сечения и отрицателен, так как эта сила изгибает балку выпуклостью вверх (стремится повернуть правую часть по часовой стрелке):

М = – Fх.

Эпюра изгибающих моментов – наклонная прямая (рис. 3.2.27, в). Наибольшего по абсолютной величине значения изгибающий момент достигает в сечении заделки.

Значение поперечной силы в сечении защемленного конца совпадает с величиной опорной реакции, а значение изгибающего момента в этом сечении равно величине реактивного момента. Этими условиями можно пользоваться для проверки правильности построения эпюр в балках с одним защемленным концом.

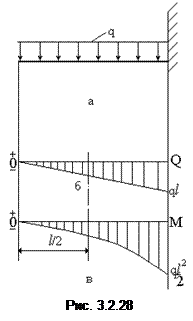Пример 3. Построим эпюры для балки с защемленным концом, к которой приложена нагрузка, равномерно-распределенная по всей длине (рис. 3.2.28, а). Пусть на единицу длины приходится нагрузка q, тогда вся нагрузка, действующая на балку, равна ql. Для этой балки также нет надобности в определении опорных реакций, если рассматривать равновесие левой части, к которой приложены только внешние активные силы.

В любом поперечном сечении балки на растоянии х от свободного конца поперечная сила равна алгебраической сумме всех сил, действующих на левую часть, т.е. равнодействующей Q = – qx равномерно распределенной нагрузки q на участке длиной х. Она отрицательная, так как нагрузка qx направлена слева от сечения вниз, т.е. стремится опустить левую часть.

Эпюра поперечных сил (рис. 3.2.28, б) представляет собой прямую наклонную линию, которую можно построить, зная две точки. При х = 0 Q = 0; при х = l Q = – ql. Наибольшее по абсолютной величине значение поперечной силы Q = – ql в сечении защемления. Изгибающий момент в произвольном сечении определяется по формуле

M = – qx = – q .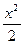

Так как сила qх изгибает балку выпуклостью вверх, изгибающий момент отрицателен.

Эпюра изгибающих моментов – парабола (рис. 3.2.28, в). Давая х различные значения, можно построить ее по точкам.

При х = 0 М = 0; при х = l/2 М = – ql²/8; при х = l M = – ql²/2.

Наибольшего по абсолютной величине значения изгибающий момент достигает в сечении защемления.

Пример 4.Построим эпюры для двухопорной балки (рис. 3.2.29, а) нагруженной силой F в произвольном сечении. Составим уравнения равновесия. Приравняв к нулю сумму моментов всех внешних сил сначала относительно правой опоры, а затем относительно левой, найдем опорные реакции:

åM_B = 0; Fb – R_Al = 0;

åM_A = –Fa + R_Bl = 0,

откуда

R_A = Fb/l, R_B = Fa/l.

Законы изменения Q и M на участках АС и СВ различны, поэтому рассмотрим каждый участок отдельно.

Поперечная сила на всем участке АС равна реакции R_A, она постоянна по всей длине участка и положительна, так как сила R_A, действующая на левую часть, направлена вверх, т.е. поднимает левую часть, Q = R_A = .

Поперечная сила в любом сечении на участке СВ равна разности сил R_A и F и также постоянна по всей длине участка, т.е. Q = R_A – F; Q = – R_B = – .

Поперечная сила отрицательна, так как сила R_B поднимает правую часть балки. Эпюра поперечных сил показана на рис. 3.2.29, б. В сечении С, где приложена сила F, поперечная сила претерпевает разрыв на величину F и меняет знак.

Найдем выражение изгибающего момента в любом сечении на первом участке при изменении х₁ в пределах: 0 < х₁ < а:

M = R_A x₁ = .

Согласно принятому правилу знаков, момент положителен, так как сила R_A стремится повернуть левую часть вокруг сечения по часовой стрелке. Полученное для изгибающего момента уравнение определяет прямую линию, которую можно построить по двум точкам:

- при х₁ = 0, т.е. в сечении на левой опоре, М = 0;

- при х₁ = а, т.е. в сечении под силой F, .

Составим выражение изгибающего момента для любого поперечного сечения второго участка при изменении х₂ от а до l: a < x₂ < l:

M = R_Ax₂ – F(x₂ – a) = F b x₂/l – F(x₂ – a).

Знаки моментов сил поставлены в соответствии с приведенным выше правилом. Изгибающий момент на втором участке изменяется также по закону прямой линии; найдем две точки этой линии. При х₂ = а, т.е. в сечении под силой F ; при х₂ = l, т.е. в сечении на правой опоре

.

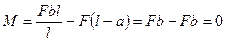Таким образом, полная эпюра изгибающих моментов при заданном нагружении представляется на каждом участке наклонной линией и имеет для балки вид треугольника (рис. 3.2.29, в). Изгибающий момент во всех сечениях положителен. Из сопоставления эпюр Q и М следует, что изгибающий момент имеет наибольшую величину в том сечении, в котором поперечная сила меняет знак. Значение этого наибольшего момента определяется по формуле

.

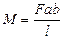Пример 5. Построим эпюры для двухопорной балки, к которой приложена равномерно распределенная нагрузка интенсивностью q (рис. 3.2.30, а). Составив и решив уравнения равновесия, найдем опорные реакции:

åM_A = 0; – ;

åM_B = 0; ,

откуда

.

Для проверки составляем сумму проекций на вертикальную ось

åY = 0; R_A – ql + R_B = 0; ql/2 – ql + ql/2 = 0.

Уравнение обращается в тождество, значит реакции вычислены верно. Проводим произвольное поперечное сечение на расстоянии х от опоры А и рассматриваем левую отсеченную часть. Поперечная сила определится из выражения

,

при x = 0 ; при x = Q = 0; при x = l .

Эпюра Q изображена на рис. 3.2.30, б.

Изгибающий момент в проведенном сечении определяется из выражения

,

при x = 0 М = 0; при х = .

Эпюра изгибающего момента изобразится параболой (рис. 3.2.30, в). Посередине балки при х = l/2 поперечная сила изменяет знак. В этом сечении изгибающий момент имеет наибольшее значение . При х = l Þ M = 0.

Пример 6.Построим эпюры поперечных сил и изгибающих моментов для простой балки, нагруженной сосредоточенной парой сил с моментом m (рис. 3.2.31, a).

Определяем опорные реакции: реакция R_A – направлена вверх, R_B – вниз. Составим уравнения суммы моментов относительно опорных точек А и B, получим

М_А = 0; –R_B l + m = 0; R_B= m/l.

М_B = 0; –R_Al + m = 0; R_A= m/l.

Опорные реакции балки образуют пару сил, момент которой уравновешивает момент приложенной пары.

Делим балку на два участка. Первый участок – от опоры А до точки приложения сосредоточенного момента; х₁ изменяется от 0 до а. Второй участок – от точки приложения момента до опоры В; х₂ изменяется от а до l. Проводим произвольное сечение на первом участке на расстоянии х₁ от опоры А и рассматриваем левую отсеченную часть. Поперечная сила на этом участке постоянна, равна реакции R_A и положительна, так как эта реакция стремится приподнять левую отсеченную часть: Q₁ = R_А = m/l.

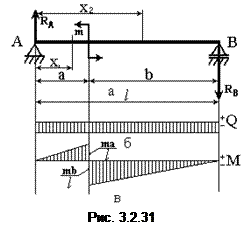Эпюра поперечных сил изображена на рис. 3.2.31,б. Изгибающий момент на первом участке зависит только от силы R_А.

M₁ = R_Аx₁ = mx₁/l.

При х₁ = 0 Þ M₁ = 0; при х₁ = а Þ M₁ = mа/l.

Момент положителен, так как сила R_А изгибает балку выпуклостью вниз. Эпюра моментов на первом участке – наклонная прямая (рис. 3.2.31, б). На втором участке – поперечная сила будет такой же, как на первом, сосредоточенный момент не влияет на поперечную силу: Q₂ = R_B = m/l.

Изгибающий момент на втором участке при рассмотрении левой отсеченной части зависит от реакции R_A и сосредоточенного момента m.

M₂ = R_Ax₂ –m = mx₂/l – m = m(x₂ – l)/l;

при х₂ = а Þ M₂ = m (a – l)/l = –m (l – a)/l = –mb/l;

при х₂ = l Þ M₂ = 0.

Эпюра моментов на втором участке (рис. 3.2.31, в), как и на первом, наклонная прямая. Под сечением, где приложена сосредоточенная пара, в эпюре моментов имеет место скачок, равный величине момента пары, так как:

ma/l + mb/l = m(a + b)/l = ml/l = m.

Взаимосвязь между нагрузками и видом эпюр поперечных сил и изгибающих моментов. Рассмотрев примеры построения эпюр поперечных сил и изгибающих моментов, можно установить следующие зависимости:

Для эпюры поперечной силы:

1. На участках, нагруженных равномерно распределенной нагрузкой, эпюра – наклонная прямая; наклон этой прямой к оси зависит от интенсивности нагрузки.

2. На участках, свободных от распределенной нагрузки, эпюра – прямая, параллельная оси балки.

3. Под сечениями балки, где приложены сосредоточенные силы, в эпюре поперечных сил имеются скачки, равные величинам приложенных сил.

4. В сечениях, где приложены сосредоточенные пары сил, значение поперечной силы не изменяется.

5. В концевых сечениях балки поперечная сила численно равна сосредоточенным силам (активным или реактивным), приложенным в этих сечениях. Если в концевых сечениях не приложены сосредоточенные силы, то поперечная сила в них равна нулю.

Для эпюры изгибающих моментов:

1. На участках, несущих равномерно распределенную нагрузку, эпюра моментов – квадратная парабола. Выпуклость параболы направлена навстречу нагрузке.

2. На участках, свободных от равномерно распределенной нагрузки, эпюра моментов – прямая линия. Под сосредоточенными силами на эпюре получаются изломы, т.е. для нескольких смежных участков эпюра изгибающих моментов – ломаная линия.

3. Под сечением балки, где приложена сосредоточенная пара сил, в эпюре изгибающих моментов имеется скачок, равный величине момента приложенной пары сил.

4. Изгибающий момент в концевых сечениях балок всегда равен нулю, если в сечениях не приложены сосредоточенные пары сил. Если в концевых сечениях приложены внешние (активные или реактивные) пары сил, то изгибающий момент в этих сечениях равен по величине моменту приложенных пар.

5. На участках, где поперечная сила равна нулю, балка испытывает чистый изгиб и эпюра изгибающих моментов – прямая, параллельная оси балки.

6. Изгибающий момент получает максимальное значение в одном из сечений балки, где изменяется знак поперечной силы.

Приведенные выводы о взаимосвязи эпюр М и Q между собой и с внешней нагрузкой позволяют обходиться без составления уравнений изгибающих моментов и поперечных сил для каждого участка балки. Достаточно вычислить ординаты эпюр для характерных сечений и соединить их линиями в соответствии с изложенными выше правилами. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (включая опорные сечения), а также сечения, ограничивающие участки с равномерно распределенной нагрузкой. Для определения максимальных значений изгибающих моментов дополнительно вычисляют моменты в сечениях, где поперечные силы равны нулю.

Построение эпюр без составления уравнений дает особенно значительный эффект для балок, нагруженных сложной нагрузкой (имеющих много участков нагружения), так как вычисления при этом менее трудоемки, чем при построении эпюр по уравнениям.

Касательные напряжения при изгибе. В случае поперечного изгиба внутренние силы в брусе уравновешивают изгибающий момент и поперечную силу. Изгибающий момент уравновешивается нормальными напряжениями, а поперечная сила – касательными, которые пропорциональны поперечной силе Q. Средняя величина этих касательных напряжений определяется по известной нам формуле

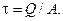
Если положить два бруса один на другой и изгибать их силой F, то каждый брус будет деформироваться независимо от другого; нижние волокна будут растягиваться, а верхние – сжиматься. По плоскости соприкосновения один брус будет скользить по другому и концевые сечения брусьев разойдутся (рис. 3.2.32, а). Чтобы заставить брусья работать как одно целое, нужно по плоскости соприкосновения приложить касательные усилия , как показано на рис. 3.2.32, б. В целом брусе верхняя часть не может сдвинуться относительно нижней; это и вызывает действие касательных усилий (напряжений) по площадкам, параллельным нейтральному слою, т.е. между горизонтальными слоями бруса.

Формула для определения касательных напряжений в балках симметричного сечения была впервые выведена русским инженером-мостостроителем Д.И. Журавским (1821-1891). Потребность в такой формуле была вызвана тем, что в XIX веке при строительстве мостов широко применялись деревянные конструкции, а балки из древесины обычно имеют прямоугольное сечение и плохо работают на скалывание вдоль волокон.

Рис. 3.2.32

Формула имеет следующий вид:

, (3.2.27)

где Q – поперечная сила в сечении;

S_х – статический момент относительно нейтральной оси части поперечного сечения, расположенной по одну сторону от рассматриваемых волокон;

J_x – момент инерции сечения относительно нейтральной оси;

b – ширина сечения на уровне волокон, где определяются напряжения.

Для прямоугольного сечения:

S_x = , J_x = ,

тогда

t = .

Так как – среднее касательное напряжение, то максимальные касательные напряжения в 1,5 раза больше средних. Касательные напряжения достигают больших значений только при 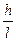> 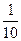. В других случаях они невелики.

Проверку прочности балки по касательным напряжениям необходимо делать при очень коротких балках и при резко меняющихся размерах сечения по высоте.

Понятия о линейных и угловых перемещениях.При изгибе сечения балки перемещаются перпендикулярно оси балки и поворачиваются вокруг своих нейтральных осей (рис. 3.2.33). Возможны случаи, когда балка, удовлетворяя условию прочности, не обладает достаточной жесткостью, т.е. прогибы и углы поворота сечения недопустимо велики.

Допустимый прогиб балок в машиностроении очень невелик. Обычно он назначается в долях от пролета балки и составляет от 1/200 до 1/1000 пролета (межопорного расстояния).

Под действием поперечных нагрузок продольная ось искривляется. Если материал подчиняется закону Гука, после снятия нагрузок брус выпрямляется, поэтому изогнутую ось бруса называютупругой линией. По форме упругой линии балки можно судить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, остается в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол.

Деформации должны иметь упругий характер, они достаточно малы. В этом случае горизонтальные перемещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые прогибами (у). Максимальные прогибы обозначают f = у_mах. Для обеспечения нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

,

где f – максимальный расчетный прогиб балки;

[f] – допускаемый прогиб.

Иногда проверяется угол поворота сечения (рис. 3.2.34).

Существует несколько методов определения перемещения сечений при изгибе. Один из них основан на дифференцировании уравнения упругой линии, более рациональный способ – использование интегралов Мора. Метод Мора – универсальный способ определения линейных и угловых перемещений в любых системах.

Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для которых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормальной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

.

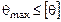Тема 7. Сложное сопротивление. Расчет по теориям прочности

Косой изгиб. Большинство ответственных деталей и узлов авиационной техники работают в условиях сложного сопротивления. Так, например, крыло самолета в целом, его лонжероны и другие элементы подвергаются одновременно изгибу и кручению. Эти же деформации испытывают фюзеляж самолета и валы передач двигателя. Узел крепления двигателя к фюзеляжу – рама, а также стойка шасси самолета работают на изгиб и растяжение – сжатие.

До сих пор мы рассматривали плоский изгиб, когда плоскость дейс­твия нагрузок совпадала с продольной плоскостью симметрии балки или вообще с одной из ее главных плоскостей. Деформация изгиба при этом происходила в плоскости действия моментов, а нейтральная ось совпадала с главной осью инерции поперечного сечения и была перпендикулярна к плоскости действия моментов. Однако бывают случаи, когда плоскость действия изгибающих моментов не совпадает ни с одной из главных плоскостей балки. Такой изгиб называется косым изгибом.

Рассмотрим пример косого изгиба. Пусть балка прямоугольного сечения, защемленная одним концом (рис. 3.2.35, а, б) изгибается силой F, действующей перпендикулярно к оси балки на свободном конце и составляющей угол с главной плоскостью ху.

Так как плоскость действия изгибающего момента в данном случае не совпадает ни с одной из главных плоскостей балки, то это будет случай косого изгиба. Абсолютное значение изгибающего момента в каком-либо сечении, отстоящем на расстоянии х от защемления, будет равна

М = F(l – х).

Разложим силу F на две составляющие F_z и F_y, действующие по главным осям сечения у и z. Тогда абсолютные значения составляющих моментов будут равны;

М_z = F_y(l – x) = F(l – x)cosa,M_y = F_z (l – x) = F(l – x)sina.

Моменты M_y и М_z действуют в главных плоскостях балки. Напряжения от каждого из этих моментов, взятых в отдельности, мы определять умеем. Пользуясь законом независимости действия сил, можно найти напряжения, получающиеся при одновременном действии моментов M_y и М_z.Таким образом, случай косого изгиба можно всегда свести к двум плоским, или, как иногда говорят, к простым изгибам.

При действии только одного момента М_z нейтральной осью будет ось z (рис. 3.2.35, в), и нормальное напряжение для какой-либо точки N с координатами z, у, взятой в первом квадранте сечения mn, определяется по формуле

s₁ = .

Напряжение в той же точке от действия только момента М_y (рис. 3.2.35, г) равно:

s₂ = .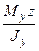

Рис. 3.2.35

При одновременном действии двух моментов М_y и M_z напряжение в любой точке сечения будет равно алгебраической сумме напряжени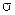й ₁ и 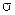₂ т.е.

s = s₁ + s₂= 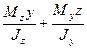. (3.2.28)

В эту формулу координаты у, z точек сечения и изгибающие моменты подставляются со своими знаками. Координаты z и у положительны в первой четверти, отрицательны в третьей четверти, во второй четверти у положительна z отрицательна, а в четвертой четверти у отрицательна, z положительна. Если момент действует так, что в рассматриваемой четверти он вызывает растяжение, то ему приписывается знак плюс, а если сжатие, то минус. Наибольшее суммарное напряжение будет в точках В и С. Абсолютные значения этих напряжений будут одинаковы. Уравнение нейтральной линии получим, приравнивая нулю правую часть формулы (3.2.28):

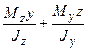= 0 или .

Этому уравнению прямой линии удовлетворяют значения у = 0 и z = 0; сле-довательно, нейтральная линия проходит через центр тяжести поперечного сечения. Определив из последнего выражения отношение у/z, найдем тангенс угла, составляемого нейтральной линией с положительным направлением оси z (рис. 3.2.35, д):

tgb= = – tga .

Из формулы видно, что для таких сечений, у которых J_y = J_z (квадрат, круг и др.), нейтральная линия всегда будет перпендикулярна к плоскости действия изгибающего момента, в которой и будет происходить деформация изгиба, не может быть косого изгиба.

Гипотезы прочности.Выше рассматривалась работа материалов при различных видах деформаций, существующих раздельно и при которых возникают напряжения или только нормальные или касательные. Напряжения при таких видах деформаций в каждой точке сечения можно складывать алгебраически.

Часто встречаются и имеют большое практическое значение случаи сочетания основных видов деформаций, когда в поперечных сечениях возникают и нормальные, и касательные напряжения, распределенные неравномерно и по разным законам. Для таких случаев опытное определение величин, характеризующих прочность, невозможно.

При оценке прочности приходится основываться на механических характеристиках материала, полученных из диаграммы растяжения, а условия прочности составляются на основе научных предположений (гипотез) о том, какой фактор вызывает появление опасного состояния. Можно полагать, что опасное состояние возникает при достижении нормальными напряжениями предела текучести или предела пропорциональности. С другой стороны, можно полагать, что опасное состояние возникает тогда, когда наибольшее относительное удлинение достигает определенного значения.

Возможно и третье предположение, что появление опасного состояния связано с тем, что касательные напряжения достигают определенного значения. Возникновение опасного состояния можно связать также с достижением определенного значения величины энергии, накапливаемой в материале при деформации.

На основе указанных выше возможных критериев опасного состояния разработано пять теорий прочности. Подробное рассмотрение этих теорий выходит за пределы нашей учебной программы. Для расчета валов, болтовых соединений, винтов домкратов и др. применяют третью или пятую теорию прочности.

Изгиб с кручением.Случаем совместного действия изгиба и кручения является передача мощности валом. Для расчета валов на совместное действие изгиба и кручения применяют третью или пятую теорию прочности.

По третьей теории прочности (теория наибольших касательных напряжений), эквивалентное напряжение вычисляют по формуле

s_экв = 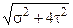. (3.2.29)

По пятой теории прочности (энергетическая теория), формула для эквивалентных напряжений имеет вид

s_экв = .^. (3.2.30)

В этих формулах и нормальное и касательное напряжения в опасной точке поперечного сечения бруса.

Максимальные нормальные и касательные напряжения у круглых валов вычисляют по формулам:

; ,

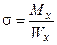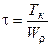где полярный момент сопротивления (W_r), и осевой момент (W_х) связаны равенством

W_r = 2W_х.

При сочетании изгиба и кручения опасными будут точки поперечного сечения вала, наиболее удаленные от нейтральной оси.

Подставим значения напряжений в принятые уравнения теорий прочности, получим

s_экв = и s_экв = .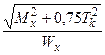

Выражение, стоящее в числителе, назовем эквивалентным моментом.

Расчетная формула для круглых валов принимает вид

s_экв = . (3.2.31)

Кручение и растяжение или сжатие.Сочетание деформаций кручения и растяжения испытывают, например, болты и крепежные винты, а сочетание кручения и сжатия – винты домкратов и т.д. Нормальные и максимальные касательные напряжения в этих случаях вычисляют по формулам

s = ; t = .

Применив третью теорию прочности, получим расчетную формулу

s_экв = . (3.2.32)

Применив пятую теорию прочности, получим

s_экв = 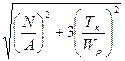. (3.2.33)

Внецентренное растяжение – сжатие. Рассмотрим нагружение бруса осевой силой F, параллельной оси, приложенной в некоторой точке Е, т.е. действующей с некоторым эксцентриситетом е. В этом случае брус испытывает внецентренное растяжение. Приложим в точке О две равные и противоположно направленные силы F¢ и F¢¢, равные F, от этого ни равновесие бруса, ни напряжения в его поперечных сечениях не изменятся.

Рассматривая отдельно эти силы, можно сделать вывод, что сила F¢ вызывает растяжение, а оставшаяся пара сил образует момент Fе, изгибающий брус.

Сила F¢, действующая по оси бруса, вызывает напряжение растяжения, которое определяется по формуле

,

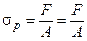это напряжение распределяется равномерно по всему поперечному сечению бруса и имеет одинаковую величину в любом сечении (рис. 3.2.36, б).

Изгибающий момент Fe постоянен по длине бруса. Он вызывает чистый изгиб, при котором возникают напряжения

.

Из рис. 3.2.36 видно, что верхние волокна бруса растягиваются силой F¢ и изгибающим моментом Fе, а нижние волокна растягиваются силой F¢ и сжимаются изгибающим моментом Fе. При этом в одной и той же плоскости возникают нормальные напряжения и, следовательно, суммарные напряжения будут равны алгебраической сумме напряжений (s_р + s_и), тогда

.

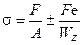Таким образом, в верхних волокнах возникают максимальные напряжения, в нижних – минимальные:

; .

Расчет тонкостенных осесимметричных оболочек. Тонкостенной осесимметричнойназывается оболочка, имеющая форму тела вращения, толщина которой весьма мала по сравнению с радиусами кривизны ее поверхности.

На рис. 3.2.37 изображена серединная (серединной называется поверхность, равноудаленная от наpужной и внутренней поверхностей оболочки) поверхность осесимметричной оболочки. Выделим из нее бесконечно малый элемент двумя меридиональными плоскостями mm₁m₂ и тт₃т₂ (т. е. плоскостями, проходящими через ось симметрии оболочки) с углом dj между ними и двумя плоскостями, перпендикулярными оси симметрии оболочки, одна из которых пересекает срединную поверхность оболочки по линии ВС, а другая по линии AD.

Радиусы кривизны срединной поверхности элемента ABCD в меридиональной плоскости обозначим r_m, а радиусы ее кривизны в плоскости, перпендикулярной меридиану, – r_q (рис. 3.2.38).

Расчеты тонкостенных осесимметричных оболочек выполняют при проектировании различных резервуаров, газгольдеров, котлов и т. д. Нагрузки, действующие на внутреннюю поверхность такой оболочки, перпендикулярны этой поверхности и симметричны относительно оси симметрии оболочки.

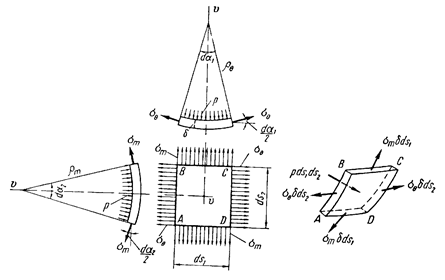
Рис. 3.2.38

Если оболочка достаточно тонкая, при расчете можно пренебречь изгибом поверхности оболочки и считать, что напряжения по толщине стенки оболочки распределены равномерно. Такой расчет называется расчетом по безмоментной теории. Если оболочка недостаточно тонкая, имеет резкие переломы в очертании, жесткие закрепления и нагружена сосредоточенными силами или моментами, то в зонах, прилегающих к местам переломов, закреплений, приложения нагрузки, а также у краев оболочки возникает изгиб. Однако по мере удаления от этих мест изгибающие моменты быстро затухают; поэтому расчет удаленных зон таких оболочек может производиться по безмоментной теории.

Элемент ABCD оболочки в ортогональных проекциях показан на рис. 3.2.38, а. По боковым граням элемента АВ и CD, совпадающим с меридиональными плоскостями, в силу симметрии оболочки и нагрузки касательные напряжения равны нулю; по этим граням действуют лишь нормальные напряжения s_q (окружные напряжения).

Из закона парности касательных напряжений следует, что касательные напряжения по боковым граням ВС и AD также равны нулю; по этим граням действуют лишь нормальные напряжения s_m (меридиональные напряжения). Кроме напряжений s_q и s_m на элемент оболочки действует нагрузка в виде давления р, перпендикулярного поверхности ABCD.

Из условия равновесия бесконечно малого элемента оболочки в виде суммы проекций приложенных к нему сил на ось v, совпадающую с нормалью к поверхности ABCD можно вывести уравнения Лапласа:

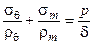, (3.2.34)

где d – толщина элемента ABCD оболочки.

Формула (3.2.34) используется для определения напряжений в стенке тонкостенной оболочки.

Из одного уравнения (2.2.34) две неизвестные величины s_q и s_m определить невозможно; поэтому напряжения в стенке оболочки можно найти лишь на основе совместного решения уравнения Лапласа и уравнения равновесия части оболочки, отсеченной конической поверхностью, перпендикулярной меридианам. Исключением является сферическая (шаровая) оболочка, находящаяся под действием газового давления; для нее

,

где D – диаметр сферы.

Вследствие центральной симметрии оболочки и действующей на нее нагрузки s_q = s_m, а потому из уравнения (3.2.34)

. (3.2.35)

Для оболочки, имеющей форму цилиндра или конуса, из уравнения Лапласа можно определить s_q, даже если s_m еще неизвестно. Это следует из того, что в указанных случаях r_m = ¥ (меридиан оболочки представляет собой прямую линию) и, значит, s_m/r_m = 0, поэтому

.

Тема 8. Устойчивость сжатых стержней

Понятие об устойчивом и неустойчивом равновесии. Относительно короткие и массивные стержни рассчитывают на сжатие, т.к. они выходят из строя в результате разрушения или остаточных деформаций. Длинные стержни небольшого поперечного сечения под действием осевых сжимающих сил изгибаются и теряют равновесие. Такие стержни работают на изгиб и сжатие.

Равновесие считают устойчивым, если за счет сил упругости после снятия внешней отклоняющей силы стержень восстановит первоначальную форму (рис. 3.2.39).

Если упругое тело после отклонения от равновесного положения не возвращается к исходному состоянию, то говорят, что произошла потеря устойчивости, а равновесие было неустойчивым.

Потерю устойчивости под действием центрально приложенной продольной сжимающей силы называют продольным изгибом.

На устойчивость равновесия влияет величина сжимающей силы.

Наибольшее значение сжимающей силы, при которой прямолинейная форма стержня сохраняет устойчивость, называют критической силой. Даже при небольшом превышении критического значения силы стержень недопустимо деформируется и разрушается.

Расчет на устойчивость. Расчет на устойчивость заключается в определении допускаемой сжимающей силы и в сравнении с ней силы действующей:

,

где F – действующая сжимающая сила;

[F] – допускаемая сжимающая сила, обеспечивающая некоторый запас устойчивости;

F_кр – критическая сила;

[s_y] – допускаемый коэффициент запаса устойчивости.

Обычно для сталей [s_y] = 1,8 – 3; для чугуна [s_y] = 5; для дерева [s_y] ≈ 2,8.

Способы определения критической силы. Расчет по формуле Эйлера. Задачу определен