
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теория механизмов и машин 3 страница

Рис. 3.3.17. Силовой анализ начального звена:
а – расчетная схема при передаче энергии через редуктор; б – план сил; в – расчетная схема при передаче энергии через муфту
Кроме уравновешивающей силы (Fy), на начальное звено действуют реакции со стороны отброшенного звена 2 (F21), а также реакция стойки (F01).
Как было упомянуто выше, F21 = – F12. Сила F12 определена предыдущим расчетом структурной группы. Таким образом, имеются неизвестная по величине и по направлению сила F01 и неизвестная по величине сила Fy.
Сила Fy определяется из уравнения
 , (3.3.27)
, (3.3.27)
откуда:

где  – момент силы F21 относительно точки О;
– момент силы F21 относительно точки О;
hy – плечо силы Fy (см. рис. 3.3. 17, а).
Реакция стойки определяется из уравнения:
 . (3.3.28)
. (3.3.28)
Строим векторное уравнение в виде плана сил, замыкающая сторона треугольника изображает реакцию F01 стойки (рис. 3.3.17, б).
В том случае, если передача энергии осуществляется через муфту, внешний силовой фактор представляет собой момент Му (рис. 3.3.21, в). Отброшенное звено 2 заменяем реакцией F21. Если на звено 1 не действуют никакие другие силы, то F01 = –F21, Му = M0(F21).
Определение уравновешивающей силы методом Жуковского.При определении мощности двигателя, расчете маховика на ведущем валу и в других подобных задачах необходимо знать только уравновешивающую силу, приложенную к начальному звену. Реакции в кинематических парах при этом определять не требуется. В таких случаях применяется метод Жуковского. Теорема Жуковского основана на известном из теоретической механики принципе возможных перемещений: сумма элементарных работ внешних сил на их возможных перемещениях равна нулю.
Пусть F1, F2, ..., Fn – внешние силы и силы инерции, приложенные к звеньям механизма; dS1, dS2, ..., dSn – проекции элементарных перемещений на направления соответствующих сил.
Тогда на основании принципа возможных перемещений запишем

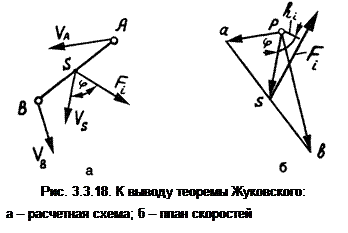 Для определения элементарной работы силы на ее элементарном перемещении рассмотрим звено АВ, в точке S которого приложена сила Fi под углом j к скорости точки S (рис. 3.3.18, а).
Для определения элементарной работы силы на ее элементарном перемещении рассмотрим звено АВ, в точке S которого приложена сила Fi под углом j к скорости точки S (рис. 3.3.18, а).
Строим план скоростей в масштабе mV, считая, что скорости точек VA и VB известны. Скорость точки S определяем по принципу подобия (рис. 3.3.18, б).
Силу Fi повернем на 90° в любую сторону и перенесем на план скоростей в точку S. Плечо этой силы относительно полюса обозначим через hi.
Определим работу силы на элементарном перемещении:
 ,
,
но
dSi = Vsdt = ps mv dt,
поэтому
 .
.
Момент силы Fi относительно полюса плана скоростей:
 .
.
Окончательно имеем

С учетом принципа возможных перемещений суммируем элементарные работы и приравниваем их к нулю:
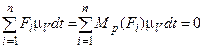 . (3.3.29)
. (3.3.29)
Сокращая выражение (3.3.29) на  , получим
, получим
 . (3.3.30)
. (3.3.30)
Выражение (3.3.30) и представляет собой теорему Жуковского, которая формулируется следующим образом: сумма моментов всех внешних сил, приложенных в соответствующих точках плана скоростей и повернутых на 90° относительно полюса плана скоростей, равна нулю.
Поворачивать можно либо силы, либо план скоростей. Иначе говоря, повернутый план скоростей можно представить как жесткий рычаг, находящийся в равновесии под действием приложенных внешних сил. Поэтому данную теорему иногда еще называют теоремой о жестком рычаге Жуковского. Пользуясь ею, можно сразу находить уравновешивающую силу, минуя силовой расчет структурных групп.
Предположим, что заданы силы, действующие на звенья механизма, – F1, F2, ..., Fn. Требуется найти уравновешивающую силу – Fу. Плечи сил, перенесенных в соответствующие точки повернутого на 90° плана скоростей, относительно полюса (hl, h2, ...., hn, hy) находят непосредственным измерением.
Тогда, согласно теореме Жуковского,

отсюда
 . (3.3.31)
. (3.3.31)
Если к звеньям механизма приложены еще и моменты, то их раскладывают на пары сил, приложенные в точках, скорости которых известны.
Тема 5. Динамический анализ машин и механизмов
Динамика – раздел механики машин и механизмов, изучающий закономерности движения звеньев механизма под действием приложенных к ним сил. Существует определение, по которому «динамика рассматривает силы в качестве причины движения тел».
В основе динамики лежат три закона, сформулированные Ньютоном, из которых следует:
1. Если равнодействующая всех внешних сил, действующих на механическую систему равно нулю, то система находится в состоянии покоя (из первого закона).
2. Изменение состояния движения механической системы может быть вызвано либо изменением действующих на нее внешних сил, либо изменением ее массы (из второго закона).
Из этих же законов следует, что динамическими параметрами механической системы являются:
- инерциальные (массы (m) и моменты инерции (I));
- силовые (силы (Fij) и моменты сил (Mij));
- кинематические (линейные (a) и угловые (e) ускорения).
В общей постановке динамика – изучение каких-либо процессов или явлений в функции времени.
Динамическая модель – модель системы, предназначенная для исследования ее свойств в функции времени (или модель системы, предназначенная для исследования в ней динамических явлений).
Прямая задача динамики – определение закона движения системы при заданном управляющем силовом воздействии.
Обратная задача динамики – определение требуемого управляющего силового воздействия, обеспечивающего заданный закон движения системы.
Методы составления уравнений (динамической модели системы):
- энергетический (уравнения энергетического равновесия – закон сохранения энергия);
- кинетостатический (уравнения силового равновесия с учетом сил инерции по принципу Даламбера).
Прямая задача динамики машин.Прямой задачей динамики машины является анализ, определение закона движения механической системы под действием заданных внешних сил. При решении этой задачи параметры машинного агрегата и действующие на него внешние силы известны, необходимо определить закон движения: скорости и ускорения в функции времени или обобщенной координаты. Иначе эту задачу можно сформулировать так: заданы управляющие силы и силы внешнего сопротивления, необходимо определить обеспечиваемый ими закон движения машины. Обратная задача динамики машины – это задача синтеза управления, когда задан требуемый закон движения машины и внешние силы сопротивления, а определяются управляющие силы.
При решении задач динамики используются либо уравнения силового равновесия системы – метод кинетостатики, либо уравнения энергетического равновесия – закон сохранения энергии. Для идеальной механической системы, в которой нет потерь энергии и звенья абсолютно жесткие, этот закон можно применять в виде теоремы о изменении кинетической энергии. Согласно этой теореме, работа всех внешних сил, действующих на систему, расходуется только на изменение ее кинетической энергии. При этом потенциальные силы – силы веса – рассматриваются, как внешние:
 ,
,
где DT – изменение кинетической энергии системы;
T – текущее значение кинетической энергии системы;
Tнач – начальное значение кинетической энергии системы;
 – суммарная работа внешних сил, действующих на систему.
– суммарная работа внешних сил, действующих на систему.
Рассмотрим сложную механическую систему (рис. 3.3.19), состоящую из n подвижных звеньев, из которых r – звеньев совершают вращательное движение, j – плоское, k – поступательное. Основная подвижность системы (W) равна 1. На систему действуют внешние силы (f) и внешние моменты (m). Движение этой системы определяется изменением одной независимой обобщенной координаты. Такую систему при решении задач динамики можно заменить более простой динамической моделью. Положение звена этой модели определяется обобщенной координатой, а динамические параметры заменяются: инерционные – суммарным приведенным моментом инерции (Iпр), силовые – суммарным приведенным моментом (Мпр). Эти параметры динамической модели рассчитываются по критериям подобия модели и объекта, которые определяются соответственно из равенства правых и левых частей уравнений изменения кинетической энергии для модели и объекта, т.е.
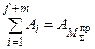 ,
,  ,
,
где  – сумма работ всех внешних сил, действующих на систему;
– сумма работ всех внешних сил, действующих на систему;
 – работа суммарного приведенного момента;
– работа суммарного приведенного момента;
 – сумма кинетических энергий звеньев системы;
– сумма кинетических энергий звеньев системы;
 – кинетическая энергия динамической модели.
– кинетическая энергия динамической модели.

Рис. 3.3.19
Понятия звена приведения и приведенных величин. Использование приведенных величин основывается на известном из кинематического анализа механизмов положении: если кинематическая цепь является механизмом, то по законам движения входных звеньев можно определить законы движения остальных его звеньев. Поэтому вместо исследования движения всех звеньев кинематической цепи механизма записывают уравнение только для звеньев приведения. Под звеном приведения понимают звено, обычно совершающее поступательное или вращательное движение. На него действуют условные силовые факторы, совершающие механическую работу, равную работе всех сил и моментов сил, действующих на звенья механизма, и оно обладает кинетической энергией, равной кинетической энергии всех звеньев механизма.
Из понятия звена приведения вытекают следующие понятия.
Приведенная сила (Fп) (момент приведенной силы (Мп)) – условная сила (момент), которая, будучи приложена в какой-либо точке звена приведения, при заданном положении входного звена совершает в единицу времени механическую работу, численно равную сумме работ всех сил и моментов сил, действующих на звенья механизма. Так как речь идет об условных силовых факторах, то обычно выбирают точку приложения приведенной силы, скорость которой известна, и направление ее вектора принимают совпадающим с направлением вектора скорости.
Из определения приведенной силы (момента) вытекают зависимости для нахождения их величин, в которых учтено, что механическая работа в единицу времени равна мощности:
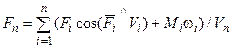 ; (3.3.32)
; (3.3.32)
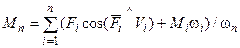 . (3.3.33)
. (3.3.33)
Приведенная масса (mп) (приведенный момент инерции (Iп)) механизма – условная масса (момент инерции), которая, будучи сосредоточена в какой-либо точке звена приведения, обладает кинетической энергией, численно равной кинетической энергии всех звеньев механизма при заданном положении входного звена.
Из этого определения следует, что величины приведенной массы и приведенного момента инерции определяются из зависимостей
 ; (3.3.34)
; (3.3.34)
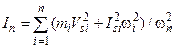 . (3.3.35)
. (3.3.35)
где Si – центр масс звена i.
Анализ выражений (3.3.32) – (3.3.35) показывает, что значения приведенной силы и ее момента, приведенной массы и приведенного момента инерции зависят только от отношения скоростей звеньев и их точек к скорости звена приведения или какой-либо его точки.
Из изучения кинематики механизмов известно, что отношения скоростей звеньев и точек определяются передаточной функцией и не зависят от абсолютных значений кинематических факторов. Поэтому в динамических расчетах шарнирных механизмов отношения скоростей для реализации зависимостей (3.3.32) – (3.3.35) определяют для единичных значений скоростей входных звеньев механизмов, а в зубчатых механизмах – через величины передаточных отношений.
Определение параметров динамической модели машины (приведение сил и масс). Рассмотрим изображенную на рис. 3.3.19 механическую систему и ее динамическую модель. Запишем для них уравнения изменения кинетической энергии.
Кинетическая энергия:
- для механической системы:  ;
;
- для модели:  .
.
Суммарная работа внешних сил:
- для механической системы:

- для модели:
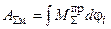 .
.
Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть для левых частей выполняется условие Тс = Тм, а для правых –  . Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений:
. Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений: 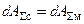 . Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:
. Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:
- для левых частей:
 ;
;
- для правых частей:
 .
.
Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции динамической модели:
 .
.
Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента динамической модели:
 .
.
Уравнения движения динамической модели.
1. Уравнение движения динамической модели в интегральной форме.
Запишем для динамической модели теорему об изменении кинетической энергии:
 ,
,
где 
Ууравнение движения динамической модели в интегральной или энергетической форме имеет вид:
 .
.
Из этого уравнения после преобразований получим формулу для расчета угловой скорости звена приведения
 .
.
Для машин, работающих в режиме пуск-останов (  и
и  ) формула принимает вид
) формула принимает вид
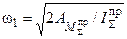 .
.
2. Уравнение движения динамической модели в дифференциальной форме.
Продифференцируем полученное выше уравнение по обобщенной координате:
 ,
,
где

 .
.
После подстановки получим уравнение движения динамической модели в дифференциальной форме
 .
.
Из этого уравнения после преобразований получим формулу для расчета углового ускорения звена приведения

Для механических систем, в которых приведенный момент не зависит от положения звеньев механизма,
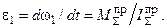
Тема 6. Колебания в механизмах
Основные понятия. Классическая теория механизмов и машин рассматривает модели механизмов с жесткими звеньями, соединенными беззазорными кинематическими парами. Реальные звенья, изготовленные из известных конструкционных материалов, обладают упругостью. В связи с этим при действии на них изменяющихся во времени силовых факторов, в том числе ударов в зазорах кинематических пар, возникают упругие деформации и связанные с ними колебания (вибрации) как самих звеньев и присоединенных конструкций, так и окружающей воздушной среды – шум. Причинами возникновения вибраций могут быть периодические изменения сил (силовое возмущение), перемещений (кинематическое возмущение) или инерционных характеристик (параметрическое возмущение).
Вибрацией (от лат. vibratio – колебание) называют механические колебания в машинах или механизмах сравнительно небольшой амплитуды. Колебание – движение или изменение состояния, обладающее той или иной степенью повторяемости или периодичностью. Механическими колебаниями(колебаниями)называется такое движение механической системы, при котором обобщенные координаты и их производные изменяются во времени, периодически возрастая или убывая (например: качание маятника или груза на пружине, движение ползуна кривошипно-ползунного механизма, колебание пластин, стержней, частей машин).
Различают следующие виды механических колебаний:
- свободные или собственные колебания – колебания, происходящие без переменного внешнего воздействия и поступления энергии извне;
- периодические – колебания, при которых значения обобщенной координаты и ее производных циклически повторяются (если это условие не выполняется, то колебания апериодические);
- вынужденные – колебания, вызываемые и поддерживаемые переменной во времени внешней силой;
- параметрические – колебания, вызываемые изменением во времени динамических параметров системы (жесткости, массы или момента инерции, демпфирования и др.);
- автоколебания – стационарные колебания, возбуждаемые и поддерживаемые за счет энергии, поступающей от источника неколебательного характера, в которой поступление энергии регулируется движением самой системы.
В ряде случаев вибрации нашли полезные применения в технике. Примерами этого являются различные вибромассажеры, вибротранспортеры и т.д.
Если источник возникновения вибраций определяется внутренними свойствами машины или механизма, то говорят о его виброактивности. Чтобы вибрации механизма не распространялись на окружающие его системы или чтобы защитить механизм от вибраций, воздействующих на него со стороны внешних систем, применяются различные методы виброзащиты. Различают внешнюю и внутреннюю виброактивность. Под внутренней виброактивностью понимают колебания, возникающие внутри механизма или машины, которые происходят по его подвижностям или обобщенным координатам. Эти колебания не оказывают непосредственного влияния на окружающую среду. При внешней виброактивности изменение положения механизма приводит к изменению реакций в опорах (т.е. связях механизма с окружающей средой) и непосредственному вибрационному воздействию на связанные с ним системы. Одна из основных причин внешней виброактивности – неуравновешенность его звеньев и механизма в целом.
Колебания каждой точки вибрирующего тела характеризуют следующие параметры:
- амплитуда виброперемещения (x0) – величина наибольшего отклонения от среднего значения;
- частота крлебаний (n) – число колебаний в единицу времени;
- частота круговая (w): w = 2pn;
- период колебаний (Т) – длительность одного цикла периодического колебательного процесса
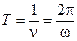 ,
,
где n – частота колебаний, Гц;
Т – период колебаний, с;
w – круговая частота, с-1.
Простейшими механическими колебаниями являются гармонические (рис. 3.3.20, а), описываемые синусоидальными (или косинусоидальными) функциями вида
х = x0 sin wt, (3.3.36)
где х – текущее отклонение рассматриваемой точки от среднего положения, м;
х0 – амплитуда колебаний, м;
w – круговая частота, с–1;
t – текущее время, с;
wt = j – фаза колебания, рад.
Уравнение (3.3.36) описывает незатухающие гармонические колебания с постоянной амплитудой и частотой. Однако чаще на практике встречаются периодические негармонические колебания, состоящие из суммы простых гармонических с различными амплитудами и частотами (рис. 3.3.20, б).

Рис. 3.3.20
 Простейшей физической моделью колебательной системы является сосредоточенная масса (m) на пружине жесткости (с), колеблющаяся без потерь в материале пружины (рис. 3.3.21).
Простейшей физической моделью колебательной системы является сосредоточенная масса (m) на пружине жесткости (с), колеблющаяся без потерь в материале пружины (рис. 3.3.21).
Свободные незатухающие колебания, возникающие при отклонении массы от положения равновесия на величину х0 и освобождении ее, связаны с периодическим высвобождением потенциальной энергии деформации пружины и переходом ее в кинетическую энергию колеблющейся массы и обратно. Они описываются уравнением гармонических колебаний системы с одной степенью свободы с постоянной амплитудой х0 и частотой w0:
 ;
;
x(t) = х0 sin(w0t + j) = х0 sin(w0t + j1),
где х0 – амплитуда виброперемещения, м;
j, j1 – начальные фазовые углы колебаний, рад:
j1 = j – p/2;
w0 – собственная круговая частота, с–1.
Собственная круговая частота зависит от физических параметров колебательной системы и определяется по формуле
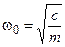 ,
,
где с – жесткость пружины, Н/м;
m – масса колеблющегося тела, кг.
Для одномассовой крутильной системы, состоящей из закрепленного одним концом вала с посаженным на свободный конец диском с моментом инерции J, дифференциальное уравнение свободных колебаний имеет вид

или
 ,
,
где

где с – крутильная жесткость, т.е. крутящий момент, требуемый для закрутки вала на угол в 1 рад.
Дифференциальное уравнение свободных колебаний с затуханием имеет вид:
 ,
,
где x – коэффициент демпфирования (Н×с/м), при этом амплитуда колебаний уменьшается до нуля.
Дифференциальное уравнение вынужденных колебаний без затухания имеет вид:
 ,
,
 ,
, 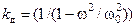 – динамический коэффициент.
– динамический коэффициент.
 .
.
Дифференциальное уравнение вынужденных колебаний с затуханием имеет вид
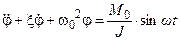 ,
,
где M0sinwt – возмущающий момент, действующий на колеблющийся диск одномассовой системы.
При рассмотрении вынужденных колебаний учет собственных колебаний особенно важен в том случае, когда числовые значения вынужденных и собственных частот равны (w = w0 (условие резонанса)) или близки друг к другу.
Резонансом называется явление сильного возрастания амплитуды колебаний при приближении частоты возбуждающей нагрузки (w) к собственной частоте (w0).
Отличительным признаком колебательной системы является вид дифференциальных уравнений ее движения: линейные и нелинейные колебания. Реальные колебательные системы всегда нелинейные, однако их часто можно описать линейными дифференциальными уравнениями.
Большое внимание привлекают к себе вибрации ВС. Основными частями ВС, изучению которых приходится уделять особое внимание, с точки зрения вибрации, являются крылья, хвостовое оперение, воздушные винты, а также двигатель. При изучении собственных колебаний крыла в пустоте, считают, что фюзеляж является абсолютно жестким телом, и крыло рассматривается, как балка с одним закрепленным и другим свободным концом. Крутильные колебания выражаются в периодическом повороте сечений крыла вокруг некоторой оси (оси жесткости). Кроме крутильных колебаний, крылья ВС подвержены также изгибным колебаниям. Когда центр тяжести и центр жесткости крыла не совпадают, то крыло совершает сложные, так называемые, изгибно-крутильные колебания.
Частоты собственных колебаний крыла ВС можно определить опытным путем. С этой целью чаще всего применяют резонансный метод определения собственных частот колебаний. Крыло с помощью специальных вибраторов подвергается действию периодической возмущающей силы, частоту которой по желанию можно изменить. Подбирая частоту возмущающей силы, при которой крыло вступает в резонанс (частота возмущающей силы станет равной частоте собственных колебаний крыла), мы определяем собственную частоту колебаний крыла. В случае колебания крыла в пустоте, без учета трения в конструкции, колебания будут гармоническими и с постоянной амплитудой.
Дата добавления: 2014-11-13; просмотров: 474; Мы поможем в написании вашей работы!; Нарушение авторских прав |