Розв’язання. Оскільки у першому випадку обидва числа додатні, то маємо Ö3+Ö5

Оскільки у першому випадку обидва числа додатні, то маємо Ö3+Ö5. У другому випадку маємо числа різних знаків, а тому Ö3+(-Ö5)=-(│-Ö5│-│Ö3│)=-(Ö5-Ö3). У третьому випадку маємо -Ö3+Ö5=+(│Ö5│-│-Ö3│)=Ö5-Ö3. Для п’ятого випадку маємо: 0,121121112…+(-0,343343334…)=-(│-0,343343334…│-│0,121121112…│)=-(0,343343334…-0,121121112…)=-0,222…=-0,(2)= - .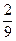

Введені означення суми дійсних чисел можна поширити на випадок будь-якої скінченної кількості доданків, але як виконувати за цими означеннями дії не зовсім зрозуміло. Саме тому спочатку введемо поняття наближеного значення нескінченного неперіодичного десяткового дробу з недостачею та з надлишком, а потім відповідні правила виконання дій. Нехай маємо дійсне число α=0,232232223… Тоді значеннями цього нескінченного неперіодичного десяткового дробу з недостачею з точністю, до цілих, десятих, сотих тощо будуть такі значення 0; 0,2; 0,23; 0,232…, а з надлишком – 1; 0,3; 0,24; 0,233 … Записати це можна за допомогою наступних подвійних нерівностей:

0≤α≤1

0,2≤α ≤0.3

0,23≤α≤0,24

…

α_n′≤α≤α_n′′

…

У цих записах α_n′- це значення дійсного числа α з недостачею, а α_n′′ - це значення дійсного числа α з надлишком.

Розглянемо два дійсних числа αі β з їхніми відповідними наближеннями α_n′≤α_n≤α_n′′ і β_n′≤β_n≤β_n′′. При розгляді властивостей числових нерівностей ми довели теорему про додавання нерівностей однакового смислу. Саме тому можна стверджувати справедливість наступної нерівності: α_n′+β_n′≤α_n+β_n≤α_n′′+β_n′′, яка дозволяє сформулювати наступне правило додавання дійсних чисел.

Правило: сума двох дійсних чисел α і β більша або дорівнює значення суми десяткових наближень цих чисел, взятих з недостачею та менша або дорівнює значення суми десяткових наближень цих чисел, взятих з надлишком.

Символічно маємо таку нерівність: α_n′+β_n′≤α_n+β_n≤α_n′′+β_n′′. Це правило можна поширити на будь-яку скінченну кількість доданків. Проілюструємо застосування цього правила на наступних прикладах.

Вправа:знайти суму дійсних чисел α=0,121121112… і β=1,242242224… з точністю до: а) цілих; б) десятих; в) сотих; г) тисячних.