Розв’язання. Десятковим наближенням числа α до тисячних з недостачею буде 0,121, а з надлишком – 0,122

Десятковим наближенням числа α до тисячних з недостачею буде 0,121, а з надлишком – 0,122. Для числа β будемо відповідно мати 1,242 і 1,243. Тепер можна за сформульованим правилом визначити значення суми чисел α і β з точністю до тисячних: 0,121•1,242≤α•β≤0,122•1,243. Отже, 0,150≤α•β≤0,152. Решту випадків пропонуємо студентам розглянути самостійно.

Виходячи із означення добутку дійсних чисел легко довести справедливість такої теореми.

Теорема: добуток дійсних чисел існує, єдиний, підкоряється комутативному та асоціативному законам і пов'язаний з дією додавання дистрибутивним законом.

Символічно цю теорему можна записати так: 1) ("α,βєR)($!γєR)(α•β=γ); 2) ("α,βєR)(α•β=β•α); 3) ("α,β,γєR)((α•β)•γ=α•(β•γ)); 4) ("α,β,γєR)(α•(β+γ)=α•β+α•γ).

Означення: часткою двох дійсних чисел α і β≠0 називають таке третє дійсне число γ, яке в добутку з числом β дає число α.

Символічно це означення можна записати так: (γ=α:β)↔(β•γ=α). Легко довести справедливість такої теореми та переконатися у справедливості наступного правила.

Теорема: частка двох дійсних чисел α і β≠0 завжди існує та єдина.

Правило:щоб знайти частку двох дійсних чисел α і β≠0 потрібно ділене помножити на число, обернене до дільника.

Символічно це виглядає так α:β=α•( ). Наприклад: Ö5:Ö3=Ö5•( ). Для практичного виконання ділення дійсних чисел, які виражені нескінченними неперіодичними десятковими дробами, використовують їхні десяткові наближення. Якщо маємо α_n′≤α_n≤α_n′′ і β_n′≤β_n≤β_n′′, де α≥0 і β≥0, то ≤ ≤ 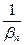. Тоді (α_n′:β_n′′)≤(α_n:β_n)≤(α_n′′:β_n′).

Правило: частка двох дійсних чисел α і β≠0 більша або дорівнює частки числа α з недостачею та числа β з надлишком і менша або дорівнює частки числа α з надлишком і числа β з недостачею.

Символічно це означення записується так: (α_n′:β_n′′)≤(α_n:β_n)≤(α_n′′:β_n). Застосування правила покажемо на наступному прикладі.

Вправа: знайти частку чисел Ö3 і Ö2 з точністю до: а) цілих; б) десятих; в) сотих.