
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическая механика
Практикум по теме «Система сходящихся сил»
 Задача 1. Ось одного из колес шасси вертолета крепится к фюзеляжу с помощью трех шарнирно закрепленных подкосов 1, 2, 3 (рис. 4.1.1). Подкос 2 расположен в плоскости XOZ, а подкос 3 – в плоскости YOZ. Колесо нагружено тремя силами: F1= 4 кН, F2 = 25 кН, F3 = 8 кН, α = 30°, β = 60°. Определите усилия в подкосах 1, 2, 3, считая, что линии действия всех сил пересекаются в точке О. Весом подкосов пренебречь.
Задача 1. Ось одного из колес шасси вертолета крепится к фюзеляжу с помощью трех шарнирно закрепленных подкосов 1, 2, 3 (рис. 4.1.1). Подкос 2 расположен в плоскости XOZ, а подкос 3 – в плоскости YOZ. Колесо нагружено тремя силами: F1= 4 кН, F2 = 25 кН, F3 = 8 кН, α = 30°, β = 60°. Определите усилия в подкосах 1, 2, 3, считая, что линии действия всех сил пересекаются в точке О. Весом подкосов пренебречь.
Ответ: S1 = 13,36 кH; S2 = – 8 кH; S3 = – 28,86 кH.
 Задача 2. Шар, масса которого равна 255 кг, подвешен с помощью кассетного держателя (рис. 4.1.2). Расстояние между шарнирами замка АС держателя (b) равна 200 мм, диаметр шара (d) равен 280 мм, высота бужа (h) равен 35 мм. Определите силу Р действия шара на замок АС и силу N – на раму держателя АВ. Весом замка АС пренебречь.
Задача 2. Шар, масса которого равна 255 кг, подвешен с помощью кассетного держателя (рис. 4.1.2). Расстояние между шарнирами замка АС держателя (b) равна 200 мм, диаметр шара (d) равен 280 мм, высота бужа (h) равен 35 мм. Определите силу Р действия шара на замок АС и силу N – на раму держателя АВ. Весом замка АС пренебречь.
Ответ: Р = 2,69 кН; N = 1 кН.
 Задача 3.Величину расчетной воздушной нагрузки, действующей на элерон (рис. 4.3) можно подсчитать по формуле: Y = kfSq, где k – коэффициент, задаваемый нормами прочности; f – коэффициент безопасности; S – площадь элерона; q – скоростной напор. Пусть Y = 7,92 кН, а отношение h/d = 1/3. Линии действия воздушной нагрузки Y и тяги управления Т взаимно перпендикулярны. Определить величину реакции в шарнире А и тягу Т.
Задача 3.Величину расчетной воздушной нагрузки, действующей на элерон (рис. 4.3) можно подсчитать по формуле: Y = kfSq, где k – коэффициент, задаваемый нормами прочности; f – коэффициент безопасности; S – площадь элерона; q – скоростной напор. Пусть Y = 7,92 кН, а отношение h/d = 1/3. Линии действия воздушной нагрузки Y и тяги управления Т взаимно перпендикулярны. Определить величину реакции в шарнире А и тягу Т.
Ответ: RA= 25,07 kH; T = 23,76 kH
 Задача 4. Аэростат с подъемной силой Q = 28 кН имеет форму шара с объемом V = 4·103 м3 (рис.4.1.4). Вес оболочки с газом и оборудования G = 8 кН приложен в центре шара. Длина троса, на котором удерживается аэростат (АВ) равен 100 м. Под действием нагрузки, равнодействующая которой проходит через центр аэростата точку О параллельно горизонтальной поверхности, шар смещается так, что его центр находится на высоте H = 100 м. Определить натяжение троса (Т) и равнодействующую силу давления ветра (F).
Задача 4. Аэростат с подъемной силой Q = 28 кН имеет форму шара с объемом V = 4·103 м3 (рис.4.1.4). Вес оболочки с газом и оборудования G = 8 кН приложен в центре шара. Длина троса, на котором удерживается аэростат (АВ) равен 100 м. Под действием нагрузки, равнодействующая которой проходит через центр аэростата точку О параллельно горизонтальной поверхности, шар смещается так, что его центр находится на высоте H = 100 м. Определить натяжение троса (Т) и равнодействующую силу давления ветра (F).
Ответ: Т = 22 кН; F = 9,16 кН.
 Задача 5.Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров. На шарнирный болт С действует вертикальная сила Р = 1000 Н (рис. 4.1.5). Определите реакции этих стержней на шарнирный болт, если углы, составляемые стержнями со стеной, равны α = 30° и β = 60°.
Задача 5.Стержни АС и ВС соединены между собой и с вертикальной стеной посредством шарниров. На шарнирный болт С действует вертикальная сила Р = 1000 Н (рис. 4.1.5). Определите реакции этих стержней на шарнирный болт, если углы, составляемые стержнями со стеной, равны α = 30° и β = 60°.
Ответ: RA = 866 Н, RB = 500 Н.
Тестовые задания по теме «Система сходящихся сил»
1. Какое действие оказывают силы на реальные тела?
а) силы изменяют форму или размеры реального тела;
б) силы изменяют движение реального тела;
в) силы изменяют характер движения и деформируют реальные тела.
2. Какое изображение вектора содержит все элементы, характеризующие силу?

3. Как взаимно расположены равнодействующая и уравновешивающая силы?
а) они направлены в одну сторону;
б) они направлены по одной прямой в противоположные стороны;
в) их взаимное расположение может быть произвольным
4. Какой многоугольник сил соответствует уравновешенной системе сходящихся сил?

5. Укажите, какой вектор силового многоугольника является равнодействующей силой.
 а) ОА;
а) ОА;
б) АВ;
в) ВС;
г) СD;
д) OD
6. Определите, будет ли находиться в равновесии тело, к которому приложены силы, направленные по одной прямой: F1 = 16 кН; F2 = -20 кН; F3 = 14 кН; F4 = -6 кН; F5 = 10 кН
а) будет;
б) не будет.
7. При каком значении угла между линиями действия двух сил  и
и 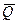 величина их равнодействующей определяется по формуле 1. R =
величина их равнодействующей определяется по формуле 1. R =  ; 2. R = P + Q; 3. R = P – Q.
; 2. R = P + Q; 3. R = P – Q.
а) 0°;
б) 90°;
в) 180°;
г) 270°;
д) 360°
8. Почему силы действия и противодействия не могут взаимно уравновешиваться?
а) эти силы не равны по модулю;
б) они не направлены в противоположные стороны;
в) они приложены к разным телам.
9. Три непараллельные силы, равные по модулю, уравновешены, Какие углы должны составлять между собой их линии действия?
а) 0°;
б) 90°;
в) 180°;
г) 120°;
д) 270°;
е) 360°.
Практикум по теме «Теория пар сил»
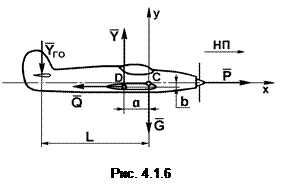 Пример.Полетный вес самолета (G) равен 30 кН, сила тяги (P) составляет 5 кН и проходит через центр тяжести самолета. Даны расстояния: a = 0,1 м; b = 0,06 м; L = 5 м. Найдите подъемную силу`(
Пример.Полетный вес самолета (G) равен 30 кН, сила тяги (P) составляет 5 кН и проходит через центр тяжести самолета. Даны расстояния: a = 0,1 м; b = 0,06 м; L = 5 м. Найдите подъемную силу`(  ), силу лобового сопротивления (
), силу лобового сопротивления ( 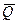 ) и силу`(
) и силу`(  ), нагружающую горизонтальное оперение, если самолет находится в равновесии (рис. 4.1.6).
), нагружающую горизонтальное оперение, если самолет находится в равновесии (рис. 4.1.6).
Решение. Рассмотрим равновесие самолета. К нему приложены две заданные силы (сила тяги (  ) и вес (
) и вес (  ) и три искомые силы (подъемная (
) и три искомые силы (подъемная (  ), сила лобового сопротивления (
), сила лобового сопротивления ( 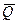 ) и сила, действующая на горизонтальное оперение`(
) и сила, действующая на горизонтальное оперение`(  ).
).
Поместим начало координат в центре тяжести самолета, в точке C, ось X направим по направлению полета, ось Y – по вертикали вверх. Имеем плоскую систему произвольно расположенных сил, составим три уравнения равновесия:

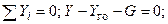

Yго = Pb + Ga / L – a = 5·0,06 + 30·0,1 /4,9 = 673 H.
Из второго уравнения:
Y = Yго + G = 30,673 кH.
 Задача 1. Руль высоты отклонен на угол d = 4°, а = 35 мм, h = 90 мм (рис. 4.1.7). На руль действует аэродинамическая сила (R), равная 3,7 кН, перпендикулярная плоскости хорд руля. Определите усилие в тяге управления 1 и суммарную реакцию шарнира А. Весом руля пренебречь.
Задача 1. Руль высоты отклонен на угол d = 4°, а = 35 мм, h = 90 мм (рис. 4.1.7). На руль действует аэродинамическая сила (R), равная 3,7 кН, перпендикулярная плоскости хорд руля. Определите усилие в тяге управления 1 и суммарную реакцию шарнира А. Весом руля пренебречь.
Ответ: T1 = 1,44 кН; XA = – 1,18 кН; YA = – 3,7 кН.
 Задача 2.На двухконсольную горизонтальную балку действует пара сил (
Задача 2.На двухконсольную горизонтальную балку действует пара сил (  ,
,  ), на левую консоль – равномерно распределенная нагрузка интенсивности (q), а в точке D правой консоли – вертикальная нагрузка (Q). Определите реакции опор, если Р = 1 кН, Q = 2 кН, q = 2 кН/м, a = 0,8 м (рис. 4.1.8).
), на левую консоль – равномерно распределенная нагрузка интенсивности (q), а в точке D правой консоли – вертикальная нагрузка (Q). Определите реакции опор, если Р = 1 кН, Q = 2 кН, q = 2 кН/м, a = 0,8 м (рис. 4.1.8).
Ответ: RA = 1,5 кН; RB = 2,1 кН.
 Задача 3. Определите реакции заделки консольной балки, изображенной на рисунке и находящейся под действием равномерно распределенной нагрузки, сосредоточенной силы и пары сил (рис. 4.1.9).
Задача 3. Определите реакции заделки консольной балки, изображенной на рисунке и находящейся под действием равномерно распределенной нагрузки, сосредоточенной силы и пары сил (рис. 4.1.9).
Ответ: Х = 2,8 кН; Y = 1,7 кН; М = –5,35 кН∙м
 Задача 4.Однородная балка AB весом (P) 100 Н прикреплена к стене шарниром А и удерживается под углом 45° к вертикали при помощи троса, перекинутого через блок и несущего груз G. Ветвь BC троса образует с вертикалью угол, равный 30°. В точке D к балке подвешен груз весом 200 Н. Определите вес груза G и реакцию шарнира А, пренебрегая трением на блоке, если BD = 0,25 AB (рис. 4.1.10).
Задача 4.Однородная балка AB весом (P) 100 Н прикреплена к стене шарниром А и удерживается под углом 45° к вертикали при помощи троса, перекинутого через блок и несущего груз G. Ветвь BC троса образует с вертикалью угол, равный 30°. В точке D к балке подвешен груз весом 200 Н. Определите вес груза G и реакцию шарнира А, пренебрегая трением на блоке, если BD = 0,25 AB (рис. 4.1.10).
Ответ: G = 146 Н; XA = 73 Н; YA = 173 Н.
 Задача 5. Руль направления закреплен в подпятнике О и подшипнике А. В центре давления С с координатами x1 = 0,1 м, y1 = 0,5 м, z1 = 0 м приложена сила бокового давления воздуха P = 2 кН, перпендикулярная плоскости руля. Определите опорные реакции (рис. 4.1.11).
Задача 5. Руль направления закреплен в подпятнике О и подшипнике А. В центре давления С с координатами x1 = 0,1 м, y1 = 0,5 м, z1 = 0 м приложена сила бокового давления воздуха P = 2 кН, перпендикулярная плоскости руля. Определите опорные реакции (рис. 4.1.11).
Ответ: R = Rz = 2 кН; Мx = 1 кН∙м; Мy = 0,2 кН∙м.
 Задача 6.Самолет, полетный вес (G) которого составляет 30 кН, совершает равномерный прямолинейный полет с набором высоты под углом 10° к горизонту. Расстояния от линий действия сил до центра масс: а = 0,1 м, b = 0,06 м, l = 5 м (рис. 4.1.12). Тяга (T), равная 8,5 кН, проходит через центр масс самолета, линия действия силы лобового сопротивления ей параллельна, а подъемная сила и сила, действующая на горизонтальное оперение, перпендикулярны направлению движения. Найдите подъемную силу (Y), силу лобового сопротивления (Q) и силу, действующую на горизонтальное оперение (Yгo).
Задача 6.Самолет, полетный вес (G) которого составляет 30 кН, совершает равномерный прямолинейный полет с набором высоты под углом 10° к горизонту. Расстояния от линий действия сил до центра масс: а = 0,1 м, b = 0,06 м, l = 5 м (рис. 4.1.12). Тяга (T), равная 8,5 кН, проходит через центр масс самолета, линия действия силы лобового сопротивления ей параллельна, а подъемная сила и сила, действующая на горизонтальное оперение, перпендикулярны направлению движения. Найдите подъемную силу (Y), силу лобового сопротивления (Q) и силу, действующую на горизонтальное оперение (Yгo).
 Ответ: Q = 3,29 кH; Y = 32,11 кH; Yго = 52,08 кH.
Ответ: Q = 3,29 кH; Y = 32,11 кH; Yго = 52,08 кH.
Задача 7. На лонжерон киля действует сила (Р), равная 80 кН. Определите реакцию крепления лонжерона к фюзеляжу в точке А, считая крепление жесткой заделкой, при несимметричном нагружении лонжерона стабилизатора, если Y1 = 40 кН, Y2 = 70 кН, a = 2,2 м, h = 2,4 м (рис. 4.1.13).
Ответ: RAX = 80 кH; RAY = 110 кH; M = 126 кH×м.
Тестовые задания по теме «Теория пар сил»
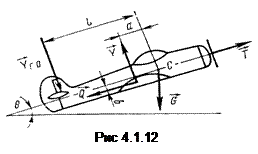
1. Определите, на каком рисунке изображена пара сил.
2. Что необходимо знать для определения эффекта действия пары сил?
а) величину силы и плечо пар
б) произведение величины силы на плечо;
в) величину момента пары и направление.
3. Как можно уравновесить пару сил?
а) одной силой;
б) парой сил.
4. Эффект действия пары сил на тело:
а) зависит от ее положения в плоскости;
б) не зависит от ее положения в плоскости.
5. Момент пары сил равен 100 Н×м, плечо пары составляет 0,2м. Определите величину сил пары.
а) 100 Н;
б) 200 Н;
в) 500 Н.
6. Как изменится величина сил пары, если плечо увеличить в два раза при сохранении величины момента?
а) уменьшится;
б) увеличится.
7. Пары сил действуют в плоскостях, перпендикулярных одной прямой. Можно ли их алгебраически складывать?
а) можно;
б) нельзя.
8. Зависят ли величина и направление момента силы относительно точки от взаимного расположения этой точки и линии действия силы?
а) не зависят;
б) зависят.
9. В каких случаях момент силы относительно оси равен нулю?
а) когда сила параллельна оси;
б) когда линия действия силы пересекает ось;
в) когда сила и ось расположены в одной плоскости.
10. Зависит ли момент присоединенной пары сил от расстояния точки приведения до линии действия силы?
а) не зависит;
б) зависит
11. Зависят ли величина и направление главного вектора от центра приведения
а) не зависит;
б) зависит.
Практикум по теме «Система произвольно расположенных сил»
Задача 1. Определите реакции опор А и В балки, находящейся под действием двух сосредоточенных сил и равномерно распределенной нагрузки. Интенсивность распределенной нагрузки, величины сил и размеры указаны на рис. 4.1.14.
Ответ: XA =2,6 кН; YA = 4,2 кН; XB = 15,6 кН.
Задача 2. Определите реакции опор А, В, С и шарнира D составной балки, изображенной на рисунке, если Q = 5 кН, Р = 6 кН; q = 1,75 кН/м (рис. 4.1.15).
Ответ: XA = 3 кН; YA = 13,8 кН; YB = –6,6 кН; YC = 10 кН; XD = 0; YD = ±5 кН.

 |
Задача 3. Вал узла привода агрегатов с зубчатыми колесами закреплен в подшипниках A и B. Радиусы колес r1 = 0,06 м и r2 = 0,1 м. На колеса действуют силы: Т1 = 3 кН и Т2 = const, параллельные оси Ax, P1 = 1,2 кН и P2 = 0,6 кН, параллельные оси Az, S = 0,9 кН, параллельная оси Ay. Линейные размеры вала: a = 0,03 м, b = 0,04 м, d = 0,06 м. Определите реакции подшипников и силу Т2. M = 1,3 кH×м (рис. 4.1.16).
Ответ: Т2 = 1,8 кН; RAX = –1,56 кН; RBX = 0,36 кН; RAY = 0,9 кН; RAZ = 1,92 кН; RBZ = –0,12 кН.
 Задача 4. С помощью ворота, схематически изображенного на рис. 4.1.17, удерживается груз Q = 1 кН. Радиус барабана (R), равна 5 см. Длина рукоятки (KD), равна 40 см; AD = 30 см; AC = 40 см; CB = 60 см. Веревка сходит с барабана по касательной, наклоненной к горизонту под углом, равным 60°. Определите давление (P) на рукоятку и реакции опор A и B при том положении ворота, когда рукоятка KD горизонтальна (рис. 4.1.17).
Задача 4. С помощью ворота, схематически изображенного на рис. 4.1.17, удерживается груз Q = 1 кН. Радиус барабана (R), равна 5 см. Длина рукоятки (KD), равна 40 см; AD = 30 см; AC = 40 см; CB = 60 см. Веревка сходит с барабана по касательной, наклоненной к горизонту под углом, равным 60°. Определите давление (P) на рукоятку и реакции опор A и B при том положении ворота, когда рукоятка KD горизонтальна (рис. 4.1.17).
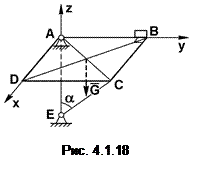 Ответ: Р = 125 Н; XA = –300 Н; ZA = –357 Н; XB = –200 Н; ZB = –384.
Ответ: Р = 125 Н; XA = –300 Н; ZA = –357 Н; XB = –200 Н; ZB = –384.
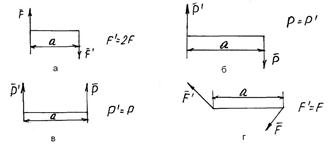
Задача 5.Однородная прямоугольная пластина ABCD со сторонами AB = CD = 0,4 м, b = 0,5 м и весом G = 10 кН закреплена в точке А при помощи шарового шарнира, а в точке В при помощи цилиндрического шарнира или же двумя цилиндрическими шарнирами в точках А и В. Кроме того, пластина поддерживается в равновесном положении стержнем ЕС, прикрепленным к пластине и неподвижной опоре при помощи шарниров. Сторона АВ горизонтальна (рис. 4.1.18). Определите реакции опор А и В и усилие в стержне ЕС, пренебрегая его весом, при a = 30°.
Ответ: ХА = 6,24 кН; YA = 5 кН; ZA = 32,8 кН; XB = 0; ZB = –8,92 кН.
Тестовые задания по теме «Система произвольно
расположенных сил»
1. Зависят ли величина и направлениеглавного вектора от положения центра приведения?
а) не зависит;
б) зависит.
2. Зависят ли величина и знак главного момента от положения центра приведения?
а) не зависят;
б) зависят.
3. В каком случае главный вектор произвольной пространственной системы сил совпадает с ее равнодействующей?
а) когда главный момент не равен нулю;
б) когда главный момент равен нулю.
4. При каком значении главного вектора 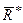 и главного момента М0 система сил находится в равновесии?
и главного момента М0 система сил находится в равновесии?
а) при  М0 = 0;
М0 = 0;
б) при 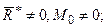
в) при  М0 = 0;
М0 = 0;
г) при 
5. Укажите, какой вид опоры соответствует данным рисункам. Изобразите эти опоры.

а) подвижная;
б) заделка;
в) неподвижная.
6. Можно ли утверждать, что система сил находится в равновесии, если главный вектор и главный момент системы сил равны нулю?
а) можно;
б) нельзя.
7. Как должна быть направлена ось х относительно прямой, проходящей через точки А и В, если уравнения равновесия имеют вид ΣМА = 0, ΣМВ = 0, ΣХi = 0?
а) прямая АВ перпендикулярна оси х;
б) прямая АВ не перпендикулярна оси х.
8. Как должна быть расположена точка А, относительно которой сумма моментов всех сил равна нулю, если уравнения равновесия имеют вид ΣМА = 0, ΣХi = 0, ΣYi = 0?
a) точка А может быть расположена в любом месте плоскости действия сил,
б) точка А – пересечение осей х и Y.
9. Могут ли точки А, В и С располагаться на одной прямой, если в качестве уравнений равновесия приняты уравнения ΣМА = 0, ΣМВ = 0, ΣМС = 0?
а) могут;
б) не могут.
Практикум по теме «Центр параллельных сил и центр тяжести»
Задача 1. Вес киля (G1), равен 5000 H, а вес руля поворота (G2), равен 1000 H (рис. 4.1.19) а = 1,8 м, b = 0,5 м, с = 2,5 м, d =2,0 м. Найдите координаты центра масс вертикального оперения.
Ответ: YС = 2,42 м; ХС= 1,42 м.
Задача 2. Определите положение центра тяжести площади трапециевидного полукрыла (рис. 4.1.20), считая его однородным а = 1,2 м, b =4,2 м, α = 30°, l = 2,1 м, d = 0,9 м.

Ответ: ХС = 1,818 м; YС = 0,883 м.
 Задача 3. Наибольшую аэродинамическую силу создает крыло, и изменение плеча этой силы приводит к значительному изменению момента. Поэтому важно знать положение центра масс самолета (точка С) относительно крыла – центровку самолета. Центровку определяют расстоянием от ребра атаки крыла до центра масс (рис. 4.1.21), измеренным вдоль хорды крыла и выраженным в процентах длины средней аэродинамической хорды (САХ):
Задача 3. Наибольшую аэродинамическую силу создает крыло, и изменение плеча этой силы приводит к значительному изменению момента. Поэтому важно знать положение центра масс самолета (точка С) относительно крыла – центровку самолета. Центровку определяют расстоянием от ребра атаки крыла до центра масс (рис. 4.1.21), измеренным вдоль хорды крыла и выраженным в процентах длины средней аэродинамической хорды (САХ):  , где хс – продольное расстояние от центра масс до переднего конца САХ, а bА – длина САХ. Пусть при первоначальном весе G = 78,4 кН самолет имел центровку 25 % САХ, а bA = 2,5 м. В хвостовую часть самолета на расстоянии S = 2 м от центра масс добавили груз весом 1,96 кН. Определите центровку самолета после добавления груза.
, где хс – продольное расстояние от центра масс до переднего конца САХ, а bА – длина САХ. Пусть при первоначальном весе G = 78,4 кН самолет имел центровку 25 % САХ, а bA = 2,5 м. В хвостовую часть самолета на расстоянии S = 2 м от центра масс добавили груз весом 1,96 кН. Определите центровку самолета после добавления груза.
Ответ: 
Задача 4. Полетный вес самолета (G) равен 150 кН. Длина средней аэродинамической хорды (bА) равна 3,68 м. Несколько пассажиров общим весом 3,2 кН, сидевшие в креслах впереди центра масс самолета на расстояние 3,6 м, перешли в хвостовой отсек самолета. Точка приложения их общей силы тяжести относительно старого положения центра масс составляет 5,6 м. Определите, на сколько изменится центровка самолета.
Ответ: Δх = 5 %.
 Задача 5. Если в качестве оси X выбрать продольную ось фюзеляжа, а начало отсчета поместить в носике фюзеляжа, то центровка самолета определится формулой
Задача 5. Если в качестве оси X выбрать продольную ось фюзеляжа, а начало отсчета поместить в носике фюзеляжа, то центровка самолета определится формулой  . Вес самолета без пассажиров и груза (G) равна 700 кН, расстояние от носика фюзеляжа до средней аэродинамической хорды ха = 18 м, а bA = 6 м. Центровка в этом случае
. Вес самолета без пассажиров и груза (G) равна 700 кН, расстояние от носика фюзеляжа до средней аэродинамической хорды ха = 18 м, а bA = 6 м. Центровка в этом случае  = 0,3. Допустимые пределы центровки примем равными 0,25...0,4. При загрузке на стоянке дополнительный груз (G1) весом 25 кН разместили так, что его центр масс оказался на расстоянии а = 6 м от центра масс незагруженного самолета (рис. 4.1.22). Пассажиров начали рассаживать, начиная со второго салона, и их суммарная сила тяжести (G2), равная 10 кН, в некоторый момент приложена на расстоянии l =11 м от точки С. Определите, будет ли в этом случае центровка входить в заданные пределы.
= 0,3. Допустимые пределы центровки примем равными 0,25...0,4. При загрузке на стоянке дополнительный груз (G1) весом 25 кН разместили так, что его центр масс оказался на расстоянии а = 6 м от центра масс незагруженного самолета (рис. 4.1.22). Пассажиров начали рассаживать, начиная со второго салона, и их суммарная сила тяжести (G2), равная 10 кН, в некоторый момент приложена на расстоянии l =11 м от точки С. Определите, будет ли в этом случае центровка входить в заданные пределы.
Ответ:  .
.
 Задача 6.Длина средней аэродинамической хорды (bA) равна 3,6 м. Центровка самолета в долях САХ равна 0,31 и в заданной системе координат определяется формулой
Задача 6.Длина средней аэродинамической хорды (bA) равна 3,6 м. Центровка самолета в долях САХ равна 0,31 и в заданной системе координат определяется формулой  . Вследствие выгорания топлива в полете центр масс самолета сместился вперед на Δx. При этом центровка самолета стала равной
. Вследствие выгорания топлива в полете центр масс самолета сместился вперед на Δx. При этом центровка самолета стала равной  = 0,28. Определите, на сколько сместился центр масс самолета (рис. 4.1.23).
= 0,28. Определите, на сколько сместился центр масс самолета (рис. 4.1.23).
Ответ:  м.
м.
 Практикум по теме «Понятие о трении. Виды трения»
Практикум по теме «Понятие о трении. Виды трения»
Задача 1.Лестница весом (P1) 200 H опирается на негладкие пол и борт фюзеляжа самолета круглого сечения (рис. 4.1.24), причем в точке касания она перпендикулярна радиусу. Коэффициенты трения: f1 = 0,18, f2 = 0,1. Длина лестницы (l) равна 2 м, β = 75°, α = 10°. Определите максимальный вес груза, который может поднять по лестнице человек весом (Р2) 800 Н.
Ответ: Р3 < 353,8 H.
 Задача 2.Перед разбегом самолета включение и набор тяги двигателей производится при заторможенных колесах основных опор (рис. 4.1.25). Допустимое значение коэффициента трения скольжения тормозных колес с поверхностью перед растормаживанием и троганием самолета соответствует f = 0,3. Вес самолета (G) равен 160 кН. Трением скольжения колес передней опоры пренебречь. l = 14 м, а = 0,8 м, b = 3,1 м, h = 3,6 м. Линия действия суммарной тяги двигателей (Т) параллельна горизонтальной поверхности. Определите вертикальные реакции передней и основных опор самолета. Сдвинется ли самолет с места, если суммарная тяга, набираемая двигателями (T0) равна 40 кН? Трением скольжения колес передней опоры пренебречь.
Задача 2.Перед разбегом самолета включение и набор тяги двигателей производится при заторможенных колесах основных опор (рис. 4.1.25). Допустимое значение коэффициента трения скольжения тормозных колес с поверхностью перед растормаживанием и троганием самолета соответствует f = 0,3. Вес самолета (G) равен 160 кН. Трением скольжения колес передней опоры пренебречь. l = 14 м, а = 0,8 м, b = 3,1 м, h = 3,6 м. Линия действия суммарной тяги двигателей (Т) параллельна горизонтальной поверхности. Определите вертикальные реакции передней и основных опор самолета. Сдвинется ли самолет с места, если суммарная тяга, набираемая двигателями (T0) равна 40 кН? Трением скольжения колес передней опоры пренебречь.
Ответ: N1 = 19,95 кH; N2 = 140,05 кH; самолет останется неподвижным, так как Tсдв = 42,02 кН.
Задача 3.Набор тяги двигателей перед разбегом самолета производится при заторможенных колесах основных опор. Вес самолета равен G, суммарная тяга двигателей параллельна горизонтальной поверхности и равна Т, а линейные размеры указаны в задаче 2. Определите допустимое значение коэффициента трения скольжения тормозных колес с поверхностью ВПП. Трением скольжения колес носовой опоры пренебречь.
Ответ: f > 
 Задача 4.Самолет с работающим двигателем и заторможенными колесами удерживается в равновесии при стоянке на ВПП перед взлетом. К колесам основных опор приложена пара сил с моментом М = 1 кН·м. Тормозные колодки А и В прижаты к барабану диаметром (d) 0,5 м (рис. 4.1.26). Коэффициент трения покоя между барабаном и колодками (f) равен 0,25. Определите величину силы Р, прижимающую тормозные колодки к барабану.
Задача 4.Самолет с работающим двигателем и заторможенными колесами удерживается в равновесии при стоянке на ВПП перед взлетом. К колесам основных опор приложена пара сил с моментом М = 1 кН·м. Тормозные колодки А и В прижаты к барабану диаметром (d) 0,5 м (рис. 4.1.26). Коэффициент трения покоя между барабаном и колодками (f) равен 0,25. Определите величину силы Р, прижимающую тормозные колодки к барабану.
Ответ: Р = 8 кН.
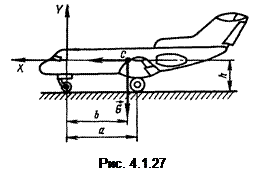 Задача 5. Вес самолета, стоящего на взлетной полосе, (G) равен 69 кН. Коэффициент трения расторможенных колес (f) равен 0,01. Продольная база шасси а = 4,8 м, а расстояние от центра масс самолета до взлетной полосы и до центра переднего колеса соответственно h = 1,3 м, b = 4,5 м (рис. 4.1.27). Диаметр колеса передней опоры (d) равен 0,5 м, и основной (D) – 0,7 м. Определите наименьшую тягу двигателя, при которой самолет придет в движение.
Задача 5. Вес самолета, стоящего на взлетной полосе, (G) равен 69 кН. Коэффициент трения расторможенных колес (f) равен 0,01. Продольная база шасси а = 4,8 м, а расстояние от центра масс самолета до взлетной полосы и до центра переднего колеса соответственно h = 1,3 м, b = 4,5 м (рис. 4.1.27). Диаметр колеса передней опоры (d) равен 0,5 м, и основной (D) – 0,7 м. Определите наименьшую тягу двигателя, при которой самолет придет в движение.
Ответ: Т = 2,18 кН.
Практикум по теме «Основные понятия кинематики.
Способы задания движения»
Задача 1. Спортивный самолет совершает в горизонтальной плоскости правильный вираж так, что его центр масс движется по окружности радиусом 680 м, время виража составляет 34 с. Найдите скорость и ускорение центра масс самолета.
Ответ: V = 125,6 м/с; a = 23,2 м/с2.
Задача 2. Самолет снижается так, что центр масс движется в вертикальной плоскости согласно уравнениям х = 1500 sin (0,05t), y = 90 + 1500 cos (0,05t), где х и y заданы в метрах, t – в секундах. Определите уравнение траектории, а также скорость и ускорение.
Ответ: х2 + (у – 90)2 = 225∙104; V = 75 м/с; a = 3,75 м/с2.
Задача 3.Уравнение движения центра масс самолета во время разбега можно представить в виде х = 0,9t2. Самолет прошел до момента отрыва путь, равный 810 м. Определите ускорение самолета, скорость отрыва и время пробега.
 Ответ: a = 1,8 м/с2; V1 = 54 м/с; t1 = 30 с.
Ответ: a = 1,8 м/с2; V1 = 54 м/с; t1 = 30 с.
Задача 4.Центр масс самолета при плавном вводе в пикирование движется в вертикальной плоскости по дуге АА1 окружности радиусом 800 м. При этом скорости самолета А и А1 дуги АА1 соответственно равны V = 150 м/с и V1 = 155 м/с. Время полета по дуге АА1 равно 5 с. Найдите касательное и нормальное ускорения центра масс самолета в точке А1, считая движение самолета равноускоренным (рис. 4.1.28).
Ответ: aτ = 1 м/с2; an = 30,3 м/с2.
Задача 5.При выходе из пикирования спортивный самолет двигался в вертикальной плоскости по окружности, начав выход на высоте Н1 = 2000 м и окончив его на высоте Н2 = 1000 м. Скорость самолета изменялась по закону V = 240 – 8t м/с. Определите касательное, нормальное и полное ускорение в момент времени t1 = 5 c, время выполнения маневра и скорость в конце пути (V1).
Ответ: aτ = –8 м/с2; an = 40 м/с2; a = 40,7 м/с2; Т = 7,5 с; V1 = 180 м/с.
 Задача 6.С вертолета, летящего с постоянной скоростью V0 = 10 м/с на высоте Н = 50 м над землей, сбрасывают груз М. Дальнейшее движение груза происходит в вертикальной плоскости с постоянным ускорением g = 9,8 м/с2. Определите траекторию груза в системе координат OXY, начало которой совпадает с положением груза в момент отделения от вертолета, расстояние, которое преодолеет груз по горизонтали до падения на землю, скорость в момент падения и угол между вектором скорости и поверхностью земли (рис. 4.1.29).
Задача 6.С вертолета, летящего с постоянной скоростью V0 = 10 м/с на высоте Н = 50 м над землей, сбрасывают груз М. Дальнейшее движение груза происходит в вертикальной плоскости с постоянным ускорением g = 9,8 м/с2. Определите траекторию груза в системе координат OXY, начало которой совпадает с положением груза в момент отделения от вертолета, расстояние, которое преодолеет груз по горизонтали до падения на землю, скорость в момент падения и угол между вектором скорости и поверхностью земли (рис. 4.1.29).
Ответ:  ; S = 32 м, V @ 32,8 м/с; a = 1,25 рад.
; S = 32 м, V @ 32,8 м/с; a = 1,25 рад.
Тестовые задания по теме «Основные понятия кинематики.
Способы задания движения»
1. Можно ли определить траекторию движения точки, если путь, пройденный точкой, задан как функция времени t (например, s = at2)?
а) можно;
б) нельзя.
2. Можно ли определить траекторию движения точки, если известно, как изменяются во времени координаты точки в прямоугольной системе координат (например, x = at2, y = bt2)?
а) можно;
б) нельзя.
3. При каком способе задания движения точки необходимо дополнительно указывать ее траекторию?
а) при любом способе задания движения;
б) при координатном способе;
в) при естественном способе.
4. Определите величину и направление скорости точки, если заданы проекции скорости на оси координат: Vx = 3 м/с, Vy = 4 м/с.
а) V = 5 м/с;
б) V = 7 м/с;
в) V = 9 м/с;
г) V = 16 м/с.
5. Точка равномерно движется по окружности. Можно ли утверждать, что полное ускорение этой точки равно нулю?
а) можно;
б) нельзя.
6. Можно ли утверждать, что поступательное движение твердого тела определяется законом движения любой его точки?
а) можно;
б) нельзя.
7. Точка движется по прямой с постоянным ускорением а = –3 м/с2. Определите, как движется точка.
а) равномерно;
б) равноускоренно;
в) равнозамедленно.
8. Какая составляющая ускорения точки характеризует изменение величины вектора скорости?
а) нормальное ускорение;
б) касательное ускорение.
Практикум по теме «Простейшие виды движения твердого тела»
Пример. При выходе на рабочий режим ротор газотурбинного авиадвигателя вращается согласно уравнению j = 200πt + 15πt2. Определите скорость и ускорение расположенного на расстоянии R = 475 мм от оси вращения центра тяжести лопатки ротора через 4 с после начала вращения.
Решение. Используя дифференциальные зависимости между углом поворота и угловой скоростью, угловой скоростью и угловым ускорением, запишем выражения
 и
и 
откуда

Найдем скорость и ускорения центра тяжести лопатки, касательное и нормальное ускорения:
V = ωR = 320π0,475 = 477,3 м/с,
at = eR = 30p0,475 = 44,8 м/с2,
аn = w2R = (320p)20,475 = 479570,9 м/с2.
При вращении тел с большими угловыми скоростями касательное ускорение точки ничтожно мало по сравнению с нормальным ускорением, поэтому принимаем ускорение центра тяжести лопатки a = an » 480 000 м/с2.
Задача 1. Винт вертолета, вращающийся с угловой скоростью ω0 = 13π рад/с, с момента выключения двигателя сделал до остановки 455 оборотов, вращаясь равнозамедленно. Определите замедление винта и сколько времени прошло с момента выключения мотора до остановки винта.
Ответ: e = 0,3 рад/с2; Т = 140 с.
Задача 2.Для проверки хода вращения турбину раскрутили с помощью стартера. Через 50 с турбина, сделав 600 оборотов, остановилась. Вращение турбины равнозамедленное. Определите начальную угловую скорость и угловое ускорение турбины.
Ответ: w0 = 151 рад/с; e = 3 рад/с2.
Задача 3. Ротор турбины авиационного двигателя вращается равноускоренно из состояния покоя таким образом, что его точка М, отстоящая от оси вращения на расстоянии 0,5 м, имеет в некоторый момент времени ускорение а = 3 м/с2, направленное под углом 45° к радиусу. Определите линейную скорость точки М в рассматриваемый момент времени и количество оборотов, выполненных турбиной за 10 с.
Ответ: V = 1,03 м/с; N = 34 об.
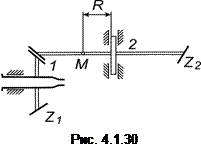 Задача 4. Ведущее зубчатое колесо l хвостового редуктора вертолета вращается с угловой скоростью w = 70π рад/с. Вращение передается на ведомое зубчатое колесо второго редуктора. Точка М колеса 2 отстоит от оси вращения на расстоянии (R), равном 0,1 м. Количество зубьев колес: z1 = 23, z2 = 53. Определите скорость и ускорение точки М (рис. 4.1.30).
Задача 4. Ведущее зубчатое колесо l хвостового редуктора вертолета вращается с угловой скоростью w = 70π рад/с. Вращение передается на ведомое зубчатое колесо второго редуктора. Точка М колеса 2 отстоит от оси вращения на расстоянии (R), равном 0,1 м. Количество зубьев колес: z1 = 23, z2 = 53. Определите скорость и ускорение точки М (рис. 4.1.30).
Ответ: V = 9,5 м/с; a = 909,8 м/с2.
 Задача 5. Для подъема грузов служит электрическая лебедка, состоящая из ведущего вала 1 с насаженной на нем шестеренкой (z1 = 20). Груз поднимается при вращении ведомого вала с шестеренкой 2 (z2 = 60). При этом канат, на котором подвешен груз Р, наматывается на барабан радиусом (R) 0,3 м. Уравнение вращения ведущего вала имеет вид j1 = 2pt2. Определить скорость и ускорение движения груза Р для момента времени t = 10 с (рис. 4.1.31).
Задача 5. Для подъема грузов служит электрическая лебедка, состоящая из ведущего вала 1 с насаженной на нем шестеренкой (z1 = 20). Груз поднимается при вращении ведомого вала с шестеренкой 2 (z2 = 60). При этом канат, на котором подвешен груз Р, наматывается на барабан радиусом (R) 0,3 м. Уравнение вращения ведущего вала имеет вид j1 = 2pt2. Определить скорость и ускорение движения груза Р для момента времени t = 10 с (рис. 4.1.31).
Ответ: V = 12,6 м/с; a = 525,85 м/с2.
Задача 6. Зубчатое колесо 1 (z1 = 80) начинает вращаться равноускоренно из состояния покоя с угловым ускорением e = p 1/c2 и приводит в движение находящееся с ним во внутреннем зацеплении колесо 2 (z2 = 20). Определить угловую скорость колеса 2 и ускорение точки В, лежащей на ободе этого колеса через 10 с после начала движения, если радиус колеса 2 равен r2 = 150 мм.
Ответ: w2 = 125,6 1/с; аВ = 2366,3 м/с2.
Тестовые задания по теме «Простейшие виды движения
твердого тела»
1. Могут ли при поступательном движении твердого тела траектории его точек быть не прямыми линиями?
а) могут;
б) не могут.
2. Можно ли утверждать, что поступательное движение твердого тела определяется законом движения любой его точки?
а) можно;
б) нельзя.
3. Определите характер вращения твердого тела вокруг неподвижной оси в следующих случаях: 1) e = 5 рад/с2; 2) e = 0; 3) w = 150 рад/с; 4) w = 20t рад/c, где t – время.
а) равномерное;
б) неравномерное.
4. Какая составляющая ускорения любой точки твердого тела равна нулю при равномерном вращении твердого тела вокруг неподвижной оси?
а) нормальнее ускорение;
б) касательное ускорение;
в) полное ускорение.
5. Определите угловую скорость вращения вала электродвигателя в рад/с, если n = 1400 об/мин.
а) 150 1/с;
б) 146,5 1/с;
в) 140 1/с.
Практикум по теме «Плоскопараллельное
(плоское) движение твердого тела»
 Задача 1. Частота вращения коленчатого вала поршневого авиадвигателя равна 2450 об/мин. Найдите мгновенный центр скоростей шатуна AB, его мгновенную угловую скорость (ω1) и скорость точки C шатуна в положении, когда поршень B находится в верхней мертвой точке. Известно, что радиус кривошипа (OA) равен 65 мм, длина шатуна составляет 260 мм, а AC = 50 мм (рис. 4.1.32)
Задача 1. Частота вращения коленчатого вала поршневого авиадвигателя равна 2450 об/мин. Найдите мгновенный центр скоростей шатуна AB, его мгновенную угловую скорость (ω1) и скорость точки C шатуна в положении, когда поршень B находится в верхней мертвой точке. Известно, что радиус кривошипа (OA) равен 65 мм, длина шатуна составляет 260 мм, а AC = 50 мм (рис. 4.1.32)
Ответ: w1 = 64 рад/с; Vc = 13,5 м/с.
Задача 2.Поршень приводится в движение при помощи кривошипного механизма с зубчатой рейкой и зубчатым сегментом. Определить скорость поршня в положении механизма, если при этом a = 30°, b = 60°, а угловая скорость кривошипа равна w0 (рис. 4.1.33).
Ответ:  .
.

Задача 3. Схема кривошипно-шатунного механизма воздушного компрессора изображена на рис. 4.1.34. Кривошип ОА длиной r = 0,01 м вращается равномерно с угловой скоростью w0 = 50p  и приводит в движение шатун АВ длиной l = 0,02 м. Определите угловую скорость и угловое ускорение шатуна, а также ускорение ползуна В в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы a = b = 45°, а расстояние ОС равно а = 0,005 м (рис. 4.1.34).
и приводит в движение шатун АВ длиной l = 0,02 м. Определите угловую скорость и угловое ускорение шатуна, а также ускорение ползуна В в момент, когда кривошип и шатун взаимно перпендикулярны и образуют с горизонтальной осью углы a = b = 45°, а расстояние ОС равно а = 0,005 м (рис. 4.1.34).
Ответ: eАВ = 6165  ; aВ = 174,75 м/с2.
; aВ = 174,75 м/с2.
Задача 4. Уравнение движения центра масс самолета, находящегося на ВПП, 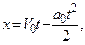 (V0, a0 = const). При этом колесо носовой опоры радиуса r катится без скольжения. Пренебрегая обжатием пневматика, определите скорость и ускорение точки на ободе колеса, которая в момент времени t1 = 30 с диаметрально противоположна точке, в которой находится мгновенный центр скоростей, если V0 = 80 м/с, a0 = 1,6 м/с2; r = 0,4 м (рис. 4.1.35).
(V0, a0 = const). При этом колесо носовой опоры радиуса r катится без скольжения. Пренебрегая обжатием пневматика, определите скорость и ускорение точки на ободе колеса, которая в момент времени t1 = 30 с диаметрально противоположна точке, в которой находится мгновенный центр скоростей, если V0 = 80 м/с, a0 = 1,6 м/с2; r = 0,4 м (рис. 4.1.35).
Ответ: VВ = 64 м/с; aВ = 2560 м/с2.
Задача 5. Колесо самолета радиусом R = 0,35 м при движении по ВПП катится без скольжения. Известно, что в некоторый момент времени скорость центра колеса А (VА) cоставляет 50 м/с, а ускорение (аА) – 6 м/с2. Определите в этот момент времени величины и направления скорости и ускорения точки В, если a = 30° (рис. 4.1.36).
Ответ: VBX = 93,3 м/с; VBY = –25 м/с; аBX = –3583 м/с2; аBY = –6174 м/с2.
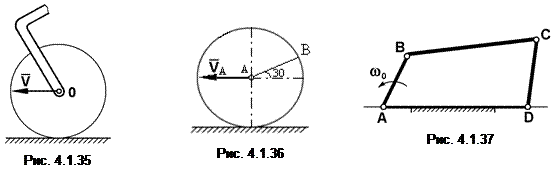 |
Задача 6. В шарнирном четырехзвеннике АВСD ведущий кривошип АВ вращается с постоянной угловой скоростью w0 = 6π рад/с. Определите мгновенные угловые скорости кривошипа CD и стержня ВС в тот момент, когда кривошип АВ и стержень ВС образуют одну прямую, если ВС = 3АВ (рис. 4.1.37).
Ответ: wBC = 2p рад/с; wCD = 0.
 Задача 7. Равносторонний треугольник АВС движется в плоскости рисунка. Ускорения вершин А и В в данный момент времени равны 16 см/с² и направлены по сторонам треугольника. Определите ускорение вершины С треугольника (рис. 4.1.38).
Задача 7. Равносторонний треугольник АВС движется в плоскости рисунка. Ускорения вершин А и В в данный момент времени равны 16 см/с² и направлены по сторонам треугольника. Определите ускорение вершины С треугольника (рис. 4.1.38).
Ответ: ускорение С направлено от вершины С к В и равно 16 см/с².
Практикум по теме «Сложное движение точки»
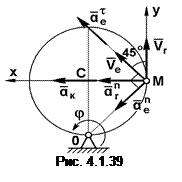 Пример.Диск радиусом 1 м вращается вокруг неподвижной оси, перпендикулярной плоскости диска, по закону j = 2/3π t3. По ободу диска перемещается точка М с относительной скоростью Vr = 10 м/с. Для момента времени t = 1 c определите абсолютную скорость и абсолютное ускорение точки М (рис. 4.1.39).
Пример.Диск радиусом 1 м вращается вокруг неподвижной оси, перпендикулярной плоскости диска, по закону j = 2/3π t3. По ободу диска перемещается точка М с относительной скоростью Vr = 10 м/с. Для момента времени t = 1 c определите абсолютную скорость и абсолютное ускорение точки М (рис. 4.1.39).
Решение. Вращение диска относительно оси О – переносное, движение точки М по ободу диска – относительное. Вектор относительной скорости (  ) направлен по касательной к траектории движения точки М. Вектор переносной скорости (
) направлен по касательной к траектории движения точки М. Вектор переносной скорости (  ) перпендикулярен отрезку ОМ в сторону вращения:
) перпендикулярен отрезку ОМ в сторону вращения:
Ve = weOM = jR  = 2πR
= 2πR  = 2
= 2  π.
π.
Абсолютная скорость находится по формуле

Модуль абсолютной скорости найдем по теореме косинусов:
 м/с
м/с
Абсолютное ускорение найдем из выражения

так как переносное движение – вращательное вокруг оси, то
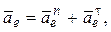
в относительном движении точка М движется по ободу диска, следовательно,

тогда полное выражение для абсолютного ускорения будет представлено в следующем виде:

Каждое из ускорений найдем по модулю и покажем по направлению (см. рис. 4.1.39):
 м/с2;
м/с2;
 м/с2;
м/с2;
 м/с2;
м/с2; 
 м/с2.
м/с2.
Для определения направления ускорения Кориолиса  повернем вектор относительной скорости
повернем вектор относительной скорости  в сторону переносного вращения на угол 90°. Проведем через точку М оси координат и, спроецировав все ускорения на оси, найдем абсолютное ускорение:
в сторону переносного вращения на угол 90°. Проведем через точку М оси координат и, спроецировав все ускорения на оси, найдем абсолютное ускорение:
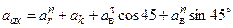 =
=  м/с2;
м/с2;
 м/с2;
м/с2;
 м/с2.
м/с2.
Задача 1. Скорость самолета по приборам в момент посадки (Vr) составляет 60 м/с. На самолет действует встречный боковой ветер под углом α = 30° к направлению ВПП. Определите абсолютную посадочную скорость самолета, направленную вдоль ВПП, и угол между относительной и абсолютной скоростями самолета, если скорость ветра (W) равна 12 м/с (рис. 4.1.40).
Ответ: Vа = 49,31 м/с; γ = 5°44'.
 Задача 2. Вертикальный подъем вертолета происходит согласно уравнению y = 0,3t2 + 6t, а уравнение вращения винта при этом имеет вид φ = 0,1t2 + 19t + φ0, где y – координата, м; φ – угол поворота, рад; t – время, с. Определите величины абсолютной скорости и абсолютного ускорения точки винта, отстоящей от оси вращения на расстоянии 0,5 м через 5 с после начала подъема.
Задача 2. Вертикальный подъем вертолета происходит согласно уравнению y = 0,3t2 + 6t, а уравнение вращения винта при этом имеет вид φ = 0,1t2 + 19t + φ0, где y – координата, м; φ – угол поворота, рад; t – время, с. Определите величины абсолютной скорости и абсолютного ускорения точки винта, отстоящей от оси вращения на расстоянии 0,5 м через 5 с после начала подъема.
Ответ: Vа = 13,5 м/с; aа = 200 м/с2.
Задача 3. Пассажирский самолет заруливает на стоянку по дуге окружности радиуса r = 20 м. Скорость самолета (Ve) равна 2 м/с. Определите переносное, кориолисово и абсолютное ускорения человека, идущего по проходу между креслами со скоростью Vr = 1 м/с вперед к носу самолета.
Ответ: ае = 0,2 м/с2; ак = 0,2 м/с2; а = 0,4 м/с2.
 Задача 4.Несущий винт вертолета приводится во вращение реактивными двигателями, расположенными на концах лопастей. Топливо подается в двигатели по трубопроводу, проложенному внутри лопастей. Скорость течения топлива (Vr) равна 0,4 м/с (рис. 4.1.41).
Задача 4.Несущий винт вертолета приводится во вращение реактивными двигателями, расположенными на концах лопастей. Топливо подается в двигатели по трубопроводу, проложенному внутри лопастей. Скорость течения топлива (Vr) равна 0,4 м/с (рис. 4.1.41).
Определите кориолисово ускорение топлива, если закон вращения ротора выражается уравнением φ = 90t, где j – угол поворота, рад; t – время, с.
Ответ: ac = 72 м/с2.
Задача 5.Диск радиусом 1 м вращается вокруг неподвижной оси, перпендикулярной плоскости диска, по закону j = 2/3pt3. По ободу диска перемещается точка М с относительной скоростью Vr = 10 м/с. Для момента времени t = 1 c определите абсолютную скорость и абсолютное ускорение точки М.
Ответ: V = 13,32 м/с; а = 40,23 м/с2.
Задача 6. Вертолет снижается вертикально согласно уравнению y = 5t + 2t2, а его несущий винт вращается по закону φ = 30t + 3t2, где y – координата, м; φ – угол поворота, рад; t – время, с. Ось Оy направлена вниз. Определите абсолютное ускорение точки лопасти винта, лежащей на расстоянии 2 м от оси вращения, в момент времени t = 2 с.
Ответ: а = 3,52 км/с2.
Практикум по теме «Динамика относительного
движения материальной точки»
Задача 1. Точка привеса математического маятника длины l движется по вертикали равноускоренно. Определите период Т малых колебаний маятника в двух случаях: когда ускорение точки привеса направлено вверх и имеет какую угодно величину р; когда это ускорение направлено вниз и величина его р < g.
Ответ: 
 .
.
Задача 2.Железнодорожный поезд идет со скоростью 15 м/с по рельсам, проложенным по меридиану с юга на север. Масса поезда равна 2000 т. Определите боковое давление поезда на рельсы: если он пересекает в данный момент северную широту 60°; если он идет в этом же месте с севера на юг.
Ответ: 3778,7 Н на правый восточный рельс; 3778,7 Н на правый западный рельс.
Задача 3. Материальная точка свободно падает в северном полушарии с высоты 500 м на Землю. Принимая во внимание вращение Земли вокруг своей оси и пренебрегая сопротивлением воздуха, определите, насколько отклонится на восток точка при падении. Географическая широта места равна 60°.
Ответ: На 12 см.
Задача 4.Горизонтальная трубка CD равномерно вращается вокруг вертикальной оси АВ с угловой скоростью ω0. Внутри трубки находится тело М. Определите скорость V тела относительно трубки в момент его вылета, если в начальный момент V = 0, х = x0, длина трубки равна L. Трением пренебречь.
Ответ:  .
.
Задача 5. Определите, как меняется ускорение силы тяжести в зависимости от широты места (j) вследствие вращения Земли вокруг своей оси. Радиус Земли (R) равен 6370 км.
Ответ:  или
или  .
.
Задача 6.Во сколько раз надо увеличить угловую скорость вращения Земли вокруг своей оси, чтобы тяжелая точка, находящаяся на поверхности Земли на экваторе, не имела бы веса? Радиус Земли (R) = 6370 км.
Ответ: В 17 раз.
Практикум по теме «Введение в динамику
системы материальных точек»
Задача 1. При выполнении «мертвой петли» самолет описывает окружность радиусом 500 м в вертикальной плоскости, двигаясь по траектории со скоростью, равной 150 м/с. Вес летчика (G) составляет 800 Н. Определите максимальную и минимальную силу, прижимающую летчика к сидению.
Ответ: Nmax= 4480 H; Nmin=2890 H.
Задача 2. Спортивный самолет совершает маневр в вертикальной плоскости, двигаясь с постоянной скоростью, равной 100 м/с. В тот момент времени, когда самолет занимает нижнее горизонтальное положение, перегрузка (n) равна 2 (перегрузка – это отношение нормального ускорения центра масс самолета к ускорению силы тяжести). Вес летчика (G) составляет 800 Н. Определите радиус кривизны траектории r и величину силы давления N летчика на сиденье в рассматриваемый момент времени.
Ответ: N = 2400 H; ρ = 510,2 м.
Задача 3. Самолет совершает правильный вираж со скоростью, равной 150 м/с, описывая в горизонтальной плоскости дугу окружности, радиус которой составляет 5683 м. Подъемная сила направлена перпендикулярно к плоскости крыла под углом γ к вертикали, а ее линия действия проходит через центр масс самолета. Определите угол крена самолета.
Ответ: ۟γ = 22°.
Задача 4.Самолет весом (G) 75 кН движется прямолинейно с набором высоты под углом a = 13° к горизонту. Суммарная тяга двигателей (T) направлена по скорости движения и равна 35 кН. Силу лобового сопротивления (Q) будем считать постоянной и равной 13 475 Н. Определите ускорение самолета и скорость через 20 с после того, как его скорость была равна V0 = 150 м/с.
Ответ: а = 0,6 м/с2; V = 162 м/c.
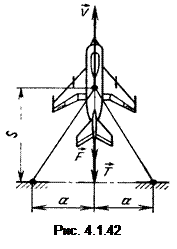 Задача 5.Для сокращения пробега в момент касания колесами ВПП истребитель цепляется за натянутый упругий трос, который, растягиваясь, создает тормозную силу T = kS, где k = 277,5 Н/м. Масса истребителя составляет 2500 кг. Общая сила сопротивления (F) составляет 25 % от веса самолета. До остановки самолет прошел 100 м. Определите посадочную скорость (рис. 4.1.42).
Задача 5.Для сокращения пробега в момент касания колесами ВПП истребитель цепляется за натянутый упругий трос, который, растягиваясь, создает тормозную силу T = kS, где k = 277,5 Н/м. Масса истребителя составляет 2500 кг. Общая сила сопротивления (F) составляет 25 % от веса самолета. До остановки самолет прошел 100 м. Определите посадочную скорость (рис. 4.1.42).
Ответ: V = 10 м/с.
Задача 6.Спортивный самолет массой 2 000 кг летит горизонтально с ускорением 5 м/с2, имея в данный момент скорость, равную 200 м/с. Сопротивление воздуха пропорционально квадратy скорости и при скорости в 1 м/с равно 0,5 Н. Считая силу сопротивления направленной в сторону, обратную скорости, определите силу тяги винта, если она составляет угол в 10° с направлением полета. Определите также величину подъемной силы в данный момент.
Практикум по теме «Теорема о движении центра масс»
Задача 1. В грузовом отсеке самолета массой М, стоящего на земле, начинают перемещать груз массой m. Перемещение осуществляется лебедкой, установленной внутри самолета, причем скорость движения груза изменяется по закону  . Определите величину горизонтальной реакции Т шасси самолета, если перемещение осуществляется в направлении продольной оси (рис. 4.1.43).
. Определите величину горизонтальной реакции Т шасси самолета, если перемещение осуществляется в направлении продольной оси (рис. 4.1.43).
Ответ: Т = mV0ke-kt.

Рис. 4.1.43
 Задача 2.На однородную призму А, лежащую на горизонтальной плоскости, положена однородная призма В (рис. 4.1.44); поперечные сечения призм – прямоугольные треугольники, масса призмы А втрое больше массы призмы В. Предполагая, что призмы и горизонтальная плоскость идеально гладкие, определите длину l, на которую передвинется призма А, когда призма В, спускаясь по А, дойдет до горизонтальной плоскости.
Задача 2.На однородную призму А, лежащую на горизонтальной плоскости, положена однородная призма В (рис. 4.1.44); поперечные сечения призм – прямоугольные треугольники, масса призмы А втрое больше массы призмы В. Предполагая, что призмы и горизонтальная плоскость идеально гладкие, определите длину l, на которую передвинется призма А, когда призма В, спускаясь по А, дойдет до горизонтальной плоскости.
Ответ: l = (a – b)/4.
 Задача 3. Два груза массой M1 и М2, соединенные нерастяжимой нитью, переброшенной через блок A, скользят по гладким боковым сторонам прямоугольного клина, опирающегося основанием ВС на гладкую горизонтальную плоскость (рис. 4.1.45). Найдите перемещение клина по горизонтальной плоскости при опускании груза M1 на высоту h = 10 см. Масса клина М = 4M1 = 16M2. Массами нити и блока пренебречь.
Задача 3. Два груза массой M1 и М2, соединенные нерастяжимой нитью, переброшенной через блок A, скользят по гладким боковым сторонам прямоугольного клина, опирающегося основанием ВС на гладкую горизонтальную плоскость (рис. 4.1.45). Найдите перемещение клина по горизонтальной плоскости при опускании груза M1 на высоту h = 10 см. Масса клина М = 4M1 = 16M2. Массами нити и блока пренебречь.
Ответ: Клин переместится вправо на 3,77 см.
Задача 4.По горизонтальной товарной платформе длиной 6 м и массой 2700 кг, находившейся в начальный момент в покое, двое рабочих перекатывают тяжелую отливку из левого конца платформы в правый. В какую сторону и насколько переместится при этом платформа, если общая масса груза и рабочих равна 1800 кг? Силами сопротивления движению платформы пренебречь.
Ответ: Налево на 2,4 м.
Задача 5. При движении самолета по ВПП из состояния покоя на колесо основной опоры действует сила F, приложенная в центре колеса, и пара сил с моментом М. Вес колеса равен G, радиус колеса составляет r, радиус инерции колеса относительно центра масс равен ρ. Коэффициент трения качения равен f. Колесо катится без скольжения. Определите закон движения центра масс колеса.
Ответ:  .
.
Практикум по теме «Теорема об изменении количества движения»
Задача 1.Груз весом (Р) 8 кН спускается на парашюте с установившейся скоростью V0 = 15 м/c. За 6 с до приземления включается тормозной двигатель, вследствие чего груз приземляется со скоростью V1 = 0,3 м/c. Какую тягу развивает тормозной двигатель?
Ответ: Т = 10 кН.
Задача 2.Парашютист весом (Р) 0,98 кН покинул самолет без вертикальной скорости и первые 5 с падал под действием только силы тяжести. После раскрытия парашюта на него начинает действовать сила сопротивления. Парашютист приземлился через 12 с, имея вертикальную составляющую скорости (Vk), равную 6 м/с. Предполагаем, что среднее значение вертикальной составляющей силы сопротивления Q = const. Определить силу Q.
Ответ: Q = 1,13 кН.
 Задача 3.По горизонтальной платформе А, движущейся по инерции со скоростью V0, перемещается тележка В (рис. 4.1.46) с постоянной относительной скоростью V1. В некоторый момент времени тележка была заторможена. Определите общую скорость V платформы с тележкой после ее остановки, если М – масса платформы, а m – масса тележки.
Задача 3.По горизонтальной платформе А, движущейся по инерции со скоростью V0, перемещается тележка В (рис. 4.1.46) с постоянной относительной скоростью V1. В некоторый момент времени тележка была заторможена. Определите общую скорость V платформы с тележкой после ее остановки, если М – масса платформы, а m – масса тележки.
Ответ:  .
.
Задача 4.Каким должен быть коэффициент трения (f) колес заторможенного автомобиля о дорогу, если при скорости движения V = 20 м/с он останавливается через 6 с после начала торможения?
Ответ: f = 0,33.
Задача 5.Истребитель, движущийся прямолинейно с постоянной скоростью V0 = 200 м/c, производит залп двумя ракетами по наземной цели по направлению, образующему угол, равный π/6 рад с направлением полета. Начальная относительная скорость снаряда U = 3V0. Вес самолета (G) составляет 49 кН, масса каждого снаряда (m) равна 60 кг. Определите горизонтальную скорость самолета в первый момент после залпа.
Ответ: V1 = 187,9 м/c.
Практикум по теме «Теорема об изменении момента
количества движения»
Задача 1. Ротор гироскопа массой 30 кг в момент выключения имел угловую скорость, равную 400p рад/с. Определите момент сил сопротивления, приложенных к ротору, относительно оси вращения, считая их постоянными, если ротор остановился через 30 мин. Осевой радиус инерции ротора равен 0,1 м.
Ответ: Мz = 0,209 Hм.
Задача 2. Турбина раскручена с помощью стартера до угловой скорости ω = 45p рад/с. Вес вращающихся частей (G) равен 3 кН, их радиус инерции относительно оси вращения (r) составляет 0,068 м, а коэффициент трения в подшипниках (f) равен 0,03. Диаметр вала равен 0,12 м. Определите время выбега турбины и количество оборотов, сделанных валом до полной остановки.
Ответ: t = 18,7 c; N = 211.
 Задача 3. Шкив массой m, имеющий радиус инерции r, затормаживается за счет прижатия к нему с силой N двух колодок. Коэффициент трения между колодками и шкивом равен f. Определите время затормаживания шкива, если в момент наложения колодок угловая скорость шкива равна ω0 (рис. 4.1.47).
Задача 3. Шкив массой m, имеющий радиус инерции r, затормаживается за счет прижатия к нему с силой N двух колодок. Коэффициент трения между колодками и шкивом равен f. Определите время затормаживания шкива, если в момент наложения колодок угловая скорость шкива равна ω0 (рис. 4.1.47).
Ответ: t = mρω0 / 2fN.
Задача 4.В процессе виража самолет движется в горизонтальной плоскости по окружности радиусом 1000 м со скоростью 100 м/с. Воздушный винт самолета весом 320 Н имеет угловую скорость, равную 80p рад/с, радиус инерции его относительно оси вращения равен 0,5 м. Найдите гироскопическое давление на подшипники А и В, в которых закреплена ось винта, если расстояние между ними (l) равно 1 м.
Ответ: NA = NB = 205 H.
Задача 5.Скорость самолета в процессе уборки шасси после отрыва от поверхности аэродрома равна 80 м/с, средняя угловая скорость шасси при их уборке (ω1) составляет 0,8 рад/с, вес колеса (G) равен 1000 H, радиус колеса составляет 0,44 м, осевой момент инерции колеса (Iz) равен 6,47 кг·м2. Определите гироскопический момент, который возникает при уборке шасси.
Ответ: М = 940 Нм.
Задача 6.Определить гироскопические реакции турбины двигателя, которые возникают в подшипниках турбины при выполнении самолетом петли Нестерова, если скорость полета на участке равна 250 м/с, средний радиус кривизны траектории петли (R) составляет 2900 м, осевой момент инерции турбины (Ix) равен 9,005 кг·м2. Угловая скорость вращения турбины (w) составляет  рад/с, расстояние между подшипниками турбины равно 0,65 м.
рад/с, расстояние между подшипниками турбины равно 0,65 м.
Ответ: N1 = N2 = 2500 H.
Практикум по теме «Теорема об изменении кинетической энергии»
Задача 1. Скорость отрыва самолета (V), движущегося прямолинейно по ВПП, равна 70 м/с. Начальная скорость равна нулю. Определите скорость самолета в той точке ВПП, для достижения которой затрачена половина всей совершенной при движении по ВПП работы.
Ответ: V1 = 35
Дата добавления: 2014-11-13; просмотров: 1199; Мы поможем в написании вашей работы!; Нарушение авторских прав