
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кинематические пары
| Обозначение | Звенья | Название | Класс |
| А | 0 – 1 | вращательная (низшая) | |
| В | 1 – 2 | вращательная (низшая) | |
| С | 2 – 3 | вращательная (низшая) | |
| D | 3 – 0 | поступательная (низшая) |
Определяем степень подвижности механизма, используя формулу П.П. Чебышева:
 ,
,
где n – число подвижных звеньев механизма;
 – число низших кинематических пар;
– число низших кинематических пар;
 – число высших кинематических пар.
– число высших кинематических пар.
Определяем структурные группы Ассура (рис. 4.3.6). Состав и последовательность присоединения групп Ассура в механизме можно выразить его формулой строения:
11(0 – 1)В ® 22(2 – 3) ВП.
Из этой формулы видно, что к структурной группе входного звена (кривошип 1) со стойкой (О) 1-го класса присоединена структурная группа 2-го класса, 2-го порядка, состоящая из шатуна 2 и ползуна 3.

Рис. 4.3.6
Построение плана механизма. Выбираем масштабный коэффициент для плана механизма:
 ,
,
где АВ – отрезок, изображающий на плане механизма звено АВ и его размер  .
.
Длину этого отрезка принимают произвольно от 30 до 70 мм.
Находим длины остальных отрезков:
 ;
;
 ;
;
 ;
;

Построения производят в следующем порядке. На чертеж (см. рис. 4.3.6) наносится ось стойки и на ней выбирается положение точки А. От горизонтальной оси откладываем угол j = 45°, тем самым показывая направление кривошипа АВ, на котором откладывается отрезок АВ = 45 мм. Далее изображается направляющая для ползуна, отстоящая от горизонтальной оси на величину y. В данном случае она совпадает с осью для стойки. Затем из точки В циркулем делается засечка радиусом ВЕ = 180 мм на оси направляющей ползуна. Точка пересечения – искомая точка Е. Аналогично находится положение точек S1 и S2: из точки А радиусом 22,5 мм делается засечка на кривошипе АВ, получается точка S1; из точки В радиусом 90 мм делается засечка на шатуне ВЕ – точка S2. Все точки соединяются прямыми линиями. План механизма построен.
Практикум по теме «Кинематический анализ и синтез механизмов»
 Пример 1.Произведем кинематический анализ шестизвенного механизма, кинематическая схема которого j1, e1, li, w1 (рис. 4.3.7). Определим vj, aj, ej, wi. Решение векторных уравнений скоростей и ускорений проводится графическим методом, часть неизвестных определяется по уравнениям кинематики плоского движения аналитически. Таким образом, для решения уравнений в задаче используется комбинированный графо-аналитический метод.
Пример 1.Произведем кинематический анализ шестизвенного механизма, кинематическая схема которого j1, e1, li, w1 (рис. 4.3.7). Определим vj, aj, ej, wi. Решение векторных уравнений скоростей и ускорений проводится графическим методом, часть неизвестных определяется по уравнениям кинематики плоского движения аналитически. Таким образом, для решения уравнений в задаче используется комбинированный графо-аналитический метод.
1. Построение плана положений. Планом положений механизма называется векторная диаграмма, на которой в масштабе изображены в виде векторов звенья механизма. Кинематические пары на плане положений не изображаются. С помощью плана положений графически решается задача о положении звеньев, определяются неизвестные линейные и угловые координаты.
 2. Построение плана скоростей (рис. 4.3.8). Определяем виды относительного движения звеньев: звено 5 движется поступательно, звенья 1, 3 совершают вращательное движение, а звенья 2, 4 – плоское.
2. Построение плана скоростей (рис. 4.3.8). Определяем виды относительного движения звеньев: звено 5 движется поступательно, звенья 1, 3 совершают вращательное движение, а звенья 2, 4 – плоское.
Линейную скорость точки B звена 1 определяем по формуле
vB = w1lAB.
На плане скорость vB изображается отрезком pvb. Зададимся величиной этого отрезка и определим масштаб плана скоростей:
mv = pvb / vB.
Для скорости точки C составим векторное уравнение сложного движения:
 ,
,
из графического решения которого находим модули векторов скоростей:
vC = pvc / mv;
vBC = bc / mv.
Скорости центров масс S2 и S3, а также скорость точки E звена 3 определяем пропорциональным делением отрезков плана скоростей :
BS2 / BC = bs2 / bc, bs2 = (BS2 / BC)bc;
DS3 / DC = ds3 / dc, ds3 = (DS3 / DC)dc;
DE3 / DC = de / dc, de = (DE3 / DC)dc.
Следовательно, vS2 = bs2 / mv, vS3 = bs3 / mv, vE = de / mv.
Для скорости точки F составим векторное уравнение сложного движения:
 ,
,
из графического решения которого находим модули векторов скоростей:
vF = pvf / mv;
vEF = ef / mv.
Угловые скорости звеньев 2 и 3 находим по формулам:
w2 = vCB / lCB;
w3 = vC / lCD.
Построение плана ускорений (рис. 4.3.9). Ускорение точки B звена 1, совершающего вращательное движение, определяем по формуле

 ,
,
где  – нормальная составляющая ускорения;
– нормальная составляющая ускорения;
 – тангенциальная составляющая ускорения.
– тангенциальная составляющая ускорения.
Задаемся величиной отрезка pan'b, изображающего на плане ускорений нормальную составляющую, и определим масштаб плана ускорений: ma = pa  /
/ 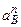 .
.
Ускорение точки C определяется совместным решением векторных уравнений сложного движения точки C относительно точки B:

и вращательного движения точки C:

где 

Тангенциальные составляющие найдем из плана ускорений:
 ,
,  .
.
Ускорение центров масс S2, S3 и точки E определим методом пропорционального деления отрезков плана ускорений:
BS2 / BC = b'  / b'c', b'
/ b'c', b'  = (BS2 / BC)b'c';
= (BS2 / BC)b'c';
DS3 / DC = d'  / d'c', d'
/ d'c', d'  = (DS3 / DC)d'c'
= (DS3 / DC)d'c'
DE3 / DC = d'e' / d'c', d'e' = (DE3 / DC)d'c';
Следовательно,
 ,
,  ,
, 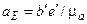 .
.
Для ускорения точки F составим векторное уравнение сложного движения:

где  = 2w3vFE – ускорение Кариолиса точки F в относительном движении относительно точки E.
= 2w3vFE – ускорение Кариолиса точки F в относительном движении относительно точки E.
Угловые ускорения звеньев 2 и 3 определяем по формулам:
 ,
,  .
.
Итак, с помощью графо-аналитического метода, мы определили угловые скорости и ускорения звеньев, а также линейные скорости и ускорения заданных точек механизма, изображенного на рис. 4.3.7.
Пример 2. Кинематический анализ механизма (рис. 4.3.10) графо-аналитическим методом.

Рис. 4.3.10:
а – план механизма m L = 0,01 м/мм; б – план ускорений mV = 19,45 м/(c2·мм); в – план скоростей mV = 0,495 м/(c·мм)
1. Построение плана скоростей. План скоростей строим в соответствии с формулой строения механизма. Определим вначале величину и направление скорости  точки В кривошипа. Величина определяется формулой
точки В кривошипа. Величина определяется формулой
 .
.
Вектор скорости перпендикулярен кривошипу АВ и направлен в сторону вращения кривошипа.
Построение начинаем с выбора полюса плана скоростей  и величины отрезка
и величины отрезка  (изображающего вектор
(изображающего вектор  ), которую выбираем в пределах 30–100 мм. Определим масштабный коэффициент плана скоростей:
), которую выбираем в пределах 30–100 мм. Определим масштабный коэффициент плана скоростей:
 .
.
Из полюса откладываем отрезок  перпендикулярно к АВ (в сторону вращения кривошипа), обозначаем конец вектора стрелкой и буквой
перпендикулярно к АВ (в сторону вращения кривошипа), обозначаем конец вектора стрелкой и буквой  (рис. 4.3.10, в).
(рис. 4.3.10, в).
Рассмотрим движение точки Е по отношению к точке В, затем по отношению к направляющей. Связь между скоростями указанных точек может быть представлена векторным уравнением
 .
.
Решаем уравнение графически. Через точку b – конец ранее найденного отрезка  плана скоростей – проводим прямую, перпендикулярную направлению ВЕ. Через полюс
плана скоростей – проводим прямую, перпендикулярную направлению ВЕ. Через полюс  проводим прямую, параллельную направляющей ползуна. Пересечение двух указанных лучей отмечаем точкой е. Отрезок
проводим прямую, параллельную направляющей ползуна. Пересечение двух указанных лучей отмечаем точкой е. Отрезок  изображает абсолютную скорость
изображает абсолютную скорость  точки Е, а отрезок
точки Е, а отрезок 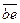 на плане скоростей изображает скорость
на плане скоростей изображает скорость  точки Е звена 2 в движении относительно точки В.
точки Е звена 2 в движении относительно точки В.
Величины этих скоростей определяют по формулам:
 м/с;
м/с;
 м/с,
м/с,
где  и
и  измеряем с плана скоростей (рис. 4.3.10, в).
измеряем с плана скоростей (рис. 4.3.10, в).
Для нахождения скоростей точек S1 и S2 воспользуемся теоремой подобия для скоростей. На стороне  откладываем отрезок
откладываем отрезок  подобный отрезку ВS1 на плане механизма и сходно с ним расположенный. Расстояние точки s1 от точки b плана скоростей найдем из отношения
подобный отрезку ВS1 на плане механизма и сходно с ним расположенный. Расстояние точки s1 от точки b плана скоростей найдем из отношения
 ,
,
 .
.
Аналогично для точки S2:  , находим
, находим  мм.
мм.
Затем методом засечек (bs1 = 25 мм, bs2 = 18 мм) определяем положение точек s1 и s2 и соединяем их с полюсом плана скоростей  . Получаем направления скоростей
. Получаем направления скоростей  и
и  . Величины этих векторов определяются формулами:
. Величины этих векторов определяются формулами:
 м/с;
м/с;
 м/с.
м/с.
Угловая скорость звена 2 определяется равенством:
 с–1.
с–1.
Для выявления направления угловой скорости звена 2 вектор скорости  мысленно переносят в точку Е звена 2 и определяют согласно движению точки Е, что w2 направлена против часовой стрелки. Указываем направление угловой скорости второго звена на плане механизма.
мысленно переносят в точку Е звена 2 и определяют согласно движению точки Е, что w2 направлена против часовой стрелки. Указываем направление угловой скорости второго звена на плане механизма.
2. Построение плана ускорений. План ускорений также выполняется в порядке, определяемом формулой строения данного механизма.
Вектор ускорения  точки В в общем случае определяется нормальной и тангенциальной составляющими:
точки В в общем случае определяется нормальной и тангенциальной составляющими:
 ,
,
где  м/с2;
м/с2;  .
.
Вектор нормального ускорения направлен вдоль прямой ВА от точки В к центру А, вектор тангенциального ускорения перпендикулярно прямой АВ. При w1 = const угловое ускорение кривошипа e1 = 0 и  .
.
На плане ускорений (рис. 4.3.10, б) выбираем полюс  и величину отрезка
и величину отрезка  (40–70 мм), изображающего вектор
(40–70 мм), изображающего вектор  . Выбираем масштабный коэффициент плана ускорений:
. Выбираем масштабный коэффициент плана ускорений:

Откладывая отрезок Pab = 70 мм ускорения точки В из полюса  параллельно направлению звена АВ (от В к А), обозначают конец стрелкой и буквой b.
параллельно направлению звена АВ (от В к А), обозначают конец стрелкой и буквой b.
Для построения плана ускорений группы (2 – 3) определяем ускорение точки Е. Составим векторное уравнение, рассматривая движение точки Е по отношению к В:
 .
.
Это уравнение содержит два неизвестных элемента: величины векторов  ,
,  .
.
При этом векторы  имеют направление (
имеют направление (  ,
,  ,
,  ), а вектор
), а вектор  и величину:
и величину:
 м/с2.
м/с2.
Через точку  ранее построенного отрезка
ранее построенного отрезка  плана ускорений проводят линию, параллельную ВЕ, и откладывают на ней отрезок
плана ускорений проводят линию, параллельную ВЕ, и откладывают на ней отрезок  , изображающий вектор ускорения
, изображающий вектор ускорения  , длина которого равна
, длина которого равна
 .
.
Далее, через точку n проводят линию, перпендикулярную ВЕ (направление вектора  ), а из полюса
), а из полюса  откладывают линию, параллельную направляющей АE. Пересечение указанных лучей обозначено точкой е. Отрезок
откладывают линию, параллельную направляющей АE. Пересечение указанных лучей обозначено точкой е. Отрезок  изображает вектор ускорения
изображает вектор ускорения  . Соединив точки b и e, получим отрезок, соответствующий ускорению
. Соединив точки b и e, получим отрезок, соответствующий ускорению  полного относительного ускорения точки Е относительно В.
полного относительного ускорения точки Е относительно В.
По теореме подобия находим длину отрезка bs2, определяющего положение точки S2 на плане ускорений из условия:
 ;
;
 мм.
мм.
Аналогично для точки S1 находим
 мм.
мм.
Методом засечек находим положение точек S1 и S2 на векторах  и
и 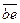 . С плана ускорений определяем величины ускорений:
. С плана ускорений определяем величины ускорений:
 ;
;
 ;
;
 ;
;
 .
.
Величину углового ускорения e2 найдем из уравнения
 .
.
Перенеся вектор  (он направлен от n к e) в точку Е плана механизма звена 2, находим направление
(он направлен от n к e) в точку Е плана механизма звена 2, находим направление  – против часовой стрелки.
– против часовой стрелки.
План ускорений построен.


Практикум по теме «Силовой анализ и расчет механизмов»
Пример 1. Кривошипно-шатунный механизм (рис. 4.74)
Силы, действующие на механизм:
- движущая сила (  ) или движущий момент (
) или движущий момент (  ) действуют на входное звено механизма от двигателя;
) действуют на входное звено механизма от двигателя;
- силы (  ) или моменты (
) или моменты (  ) полезного сопротивления;
) полезного сопротивления;
- силы тяжести звеньев (G):
 Н;
Н;
 Н;
Н;
 Н;
Н;
- силы «пассивных» сопротивлений (силы трения) (  ) или их моменты (
) или их моменты (  );
);
- силы инерции (  ) и моменты инерции (
) и моменты инерции (  ):
):
 Н,
Н,  ;
;
 Н,
Н,  ;
;
 Н,
Н,  .
.
Разбиваем механизм на структурные группы Ассура. Построим отдельно структурную группу «шатун – ползун», приложим к ней все действующие силы, включая реакции связей  и
и  , силы и моменты инерции (рис. 4.3.12).
, силы и моменты инерции (рис. 4.3.12).

Составляем уравнение моментов относительно точки Е:
 :
:  .
.
Из этой формулы можно определить тангенциальную составляющую реакции шарнира В:



Расстояния 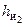 и
и  измеряем с плана данной структурной группы. Умножая их на масштабный коэффициент mL, получим реальные значения плеч соответствующих сил.
измеряем с плана данной структурной группы. Умножая их на масштабный коэффициент mL, получим реальные значения плеч соответствующих сил.
На основании принципа Даламбера составляем уравнение равновесия структурной группы «шатун – ползун»:

Из восьми значений сил, входящих в это уравнение, шесть известны по величине и направлению, а две только по направлению. Следовательно, возможно графическое решение этого уравнения. Для определения неизвестных составляющих строим план сил данной структурной группы (рис. 4.3.13).
Выбираем полюс  и величину отрезка
и величину отрезка  (10–70 мм), изображающего вектор
(10–70 мм), изображающего вектор  . Выбираем масштабный коэффициент плана сил:
. Выбираем масштабный коэффициент плана сил:

Откладывая отрезок  из полюса
из полюса  перпендикулярно направлению звена ВЕ, обозначают конец стрелкой и буквой а. Далее построения ведут в следующем порядке: в направлении действия силы
перпендикулярно направлению звена ВЕ, обозначают конец стрелкой и буквой а. Далее построения ведут в следующем порядке: в направлении действия силы  (противоположно линии действия ускорения
(противоположно линии действия ускорения  ) откладываем отрезок
) откладываем отрезок  ; из точки b в направлении действия сил
; из точки b в направлении действия сил  и
и  (вертикально вниз) откладываем отрезок
(вертикально вниз) откладываем отрезок  ; из точки с в направлении действия силы
; из точки с в направлении действия силы  (противоположно линии действия ускорения
(противоположно линии действия ускорения  ) откладываем отрезок
) откладываем отрезок  ; из точки d в направлении действия силы
; из точки d в направлении действия силы  откладываем отрезок
откладываем отрезок  .
.

Величины указанных отрезков находят по формулам:
 мм;
мм;
 мм;
мм;
 мм;
мм;
 мм.
мм.
Затем через полученную точку е проводим вертикально вверх луч, дающий направление реакции  , а через полюс плана сил проводим луч, параллельный ВЕ, дающий направление реакции
, а через полюс плана сил проводим луч, параллельный ВЕ, дающий направление реакции  . Точка пересечения этих лучей – искомая точка f. Так как
. Точка пересечения этих лучей – искомая точка f. Так как  , то соединяя точки a и f получим направление силы
, то соединяя точки a и f получим направление силы  .
.
Из плана сил определяем величины отрезков  , ef и af, а также величины соответствующих сил:
, ef и af, а также величины соответствующих сил:
 Н;
Н;

 Н.
Н.
 Теперь произведем расчет входного звена механизма. Строим структурную группу входного звена со стойкой и прикладываем к ней все действующие силы (рис. 4.3.14). Реакция
Теперь произведем расчет входного звена механизма. Строим структурную группу входного звена со стойкой и прикладываем к ней все действующие силы (рис. 4.3.14). Реакция  равна, но обратная по направлению, ранее определенной реакции
равна, но обратная по направлению, ранее определенной реакции  (
(  ). Поскольку входное звено совершает вращательное движение, то необходимо учесть уравновешивающую силу
). Поскольку входное звено совершает вращательное движение, то необходимо учесть уравновешивающую силу  , которая находится из уравнения моментов относительно оси вращения входного звена точки А.
, которая находится из уравнения моментов относительно оси вращения входного звена точки А.
 :
: 
 Н.
Н.
Уравнение равновесия для данной структурной группы имеет вид
 .
.
В этом уравнении неизвестны величина и направление реакции  .
.
 Строим план сил структурной группы входного звена (рис. 4.3.15). Последовательность построения аналогична предыдущему случаю. Выбираем длину отрезка, соответствующего силе
Строим план сил структурной группы входного звена (рис. 4.3.15). Последовательность построения аналогична предыдущему случаю. Выбираем длину отрезка, соответствующего силе  , произвольно в пределах от 30 до 100 мм. Выбираем масштабный коэффициент этого плана сил:
, произвольно в пределах от 30 до 100 мм. Выбираем масштабный коэффициент этого плана сил:

Далее находим величины отрезков, соответствующих известным силам  :
:
 мм;
мм;
 мм;
мм;
 мм.
мм.
Отрезки откладываем, начиная с полюса  , в направлении, параллельном силам, которым они соответствуют. Замыкая многоугольник (соединяя точки d и
, в направлении, параллельном силам, которым они соответствуют. Замыкая многоугольник (соединяя точки d и  ), получим направление реакции
), получим направление реакции  . Ее величину определим по формуле
. Ее величину определим по формуле
 Н.
Н.
Планы сил построены.
Пример 2. Произвести силовой расчет шестизвенного рычажного механизма
 Рассматривается кинетостатический расчет шестизвенного рычажного механизма (рис. 4.3.16). Дано mi, JSi, li, FC5, aSi, ji, ei, необходимо определить Fij, Mg1. Решение поставленной задачи осуществляется методом кинетостатики. Решение векторных уравнений сил проводится графическим методом, а уравнения моментов решаются аналитически. Таким образом, в данном примере для решения уравнений кинетостатики используется графо-аналитический метод.
Рассматривается кинетостатический расчет шестизвенного рычажного механизма (рис. 4.3.16). Дано mi, JSi, li, FC5, aSi, ji, ei, необходимо определить Fij, Mg1. Решение поставленной задачи осуществляется методом кинетостатики. Решение векторных уравнений сил проводится графическим методом, а уравнения моментов решаются аналитически. Таким образом, в данном примере для решения уравнений кинетостатики используется графо-аналитический метод.
Уравнения кинестатического равновесия:
Fi + FФi = 0; Mi + MФi = 0,
где FФi – инерционные силы, приложенные к звеньям;
MФi – моменты сил инерции, приложенные к звеньям.
1. Определение числа неизвестных при силовом расчете
Для определения числа неизвестных, а, следовательно, и числа независимых уравнений, при силовых расчетах необходимо провести структурный анализ механизма и определить число и классы кинематических пар, число основных подвижностей, число избыточных связей. Чтобы силовой расчет можно было провести, используя только уравнения кинетостатики, необходимо устранить в нем избыточные связи. В противном случае, к системе уравнений кинетостатики необходимо добавить уравнения деформации звеньев, необходимые для раскрытия статической неопределимости механизма. Так как каждая связь в КП механизма соответствует одной компоненте реакции, то число неизвестных компонент равно суммарному числу связей, накладываемых КП механизма. Уравновешивающая сила или момент должны действовать по каждой основной подвижности механизма. Поэтому суммарное число неизвестных в силовом расчете определяется суммой связей в КП механизма и его основных подвижностей:
ns = W0 + S(H – i)pi,
где ns – число неизвестных в силовом расчете.
2. Определение сил тяжести:
Gi = migi.
3. Определение главных векторов и главных моментов сил инерции:
Фi = –miaSi;
MФi = –ISiei.
4. Кинетостатический силовой расчет механизма:
4.1. Силовой расчет группы звеньев 4 – 5.
 В начале рассмотрим звено 4 (рис. 4.3.17) и запишем векторное уравнение сил:
В начале рассмотрим звено 4 (рис. 4.3.17) и запишем векторное уравнение сил:
 .
.
Из этого уравнения следует, что сила  и приложена в точке E к звену 4.
и приложена в точке E к звену 4.
Сумма моментов для звена 4 относительно точки E позволяет вычислить момент в поступательной паре E, образованный звеньями 4 и 3:
 M43 = 0.
M43 = 0.
Рассмотрим группу звеньев 4 – 5:
Векторное уравнение сил для группы звеньев 4 – 5 (рис. 4.3.18) дает возможность определить модули векторов сил F43 и F50.
 .
.
 Строим план сил в масштабе mF и находим
Строим план сил в масштабе mF и находим
F43 = ab /mF;
F50 = bpF / mF .
Для определения реактивного момента в поступательной паре Q составим уравнение моментов для звенев 4 – 5 относительно точки Q:
 ;
;
–M50 + F43hQF43 + G5lS5Q = 0.
из последнего уравнения определяем M50.
4.2. Силовой расчет группы звеньев 2 – 3 (рис. 4.3.19).
Рассмотрим звено 2:

 ;
;
–MФ2 + G2hCG2 – Ф2hCФ2 –  lBC = 0.
lBC = 0.
Из этого уравнения определяем тангенциальную составляющую  . Рассмотрим сумму моментов для группы звеньев 2 – 3 относительно точки D:
. Рассмотрим сумму моментов для группы звеньев 2 – 3 относительно точки D:
–MФ2 + G2hDG2 + Ф2hDФ2 + MФ3 –  hDF21t –
hDF21t –
–  hDF21n – G3hDG3 + Ф3hDФ3 = 0.
hDF21n – G3hDG3 + Ф3hDФ3 = 0.
Из этого уравнения определяем нормальную составляющую  .
.
Полная реакция в паре B равна:
 .
.
 Векторное уравнение сил для группы 2 – 3 позволяет графически определить вектор F30 по величине и направлению (рис. 4.3.20).
Векторное уравнение сил для группы 2 – 3 позволяет графически определить вектор F30 по величине и направлению (рис. 4.3.20).

Строим план сил в масштабе mF (см. рис. 4.3.20) и находим F30 = cpF / mF.
Рассмотрим векторное уравнение сил для звена 2:

из которого находим : F23 = dc / mF.
4.3. Силовой расчет начального звена 1 (рис. 4.3.21).
 Из векторного уравнения сил для звена 1 графически определяем вектор F10 по величине и направлению:
Из векторного уравнения сил для звена 1 графически определяем вектор F10 по величине и направлению:

Строим план сил (рис. 4.3.22) в масштабе mF и находим
F10 = cpF / mF.
 Сумма моментов для звена 1 относительно точки A дает возможность найти значение движущего момента Mд1:
Сумма моментов для звена 1 относительно точки A дает возможность найти значение движущего момента Mд1:

–F12hAF12 + Mд1 + MФ1 = 0.
Итак, с помощью графо-аналитического способа мы определили величины и направления реакций в кинематических парах, величины реактивных моментов и значение уравновешивающего момента данного механизма.
Практикум по теме «Синтез механизмов»
Пример 1. Аналитическое определение передаточного отношения.
В планетарном редукторе, изображенном на рис. 4.3.23, на звене 2 нарезаны два зубчатых венца: z2, который зацепляется с зубчатым венцом z1 звена 1; z3, который зацепляется с внутренним зубчатым венцом z4 звена 3.
По формуле Виллиса отношение угловых скоростей звеньев для внешнего зацепления колес z2 и z1:
(w1 – wh)/(w2 – wh) = –z2 / z1;
для внешнего зацепления колес z4 и z3
(w2 – wh) / (w3 – wh) = –z4 / z3.
Перемножим правые и левые части этих уравнений и получим
[(w1 – wh) / (w2 – wh)][( w2 – wh) / (w3 – wh)] = z2z4 / z1z3 ;
[(w1 – wh) / (–wh) ] = z2z4 / z1z3;
 = w1 / wh = 1 – z2z4 / z1z3.
= w1 / wh = 1 – z2z4 / z1z3.
Пример 2. Графическое определение передаточного отношения двухрядного механизма с двумя внешними зацеплениями.
В системе координат ri0V построим треугольники распределения линейных скоростей звеньев (рис. 4.3.23). Для этого из точки a c ординатой r1 в выбранном произвольном масштабе mV , мм/мс–1 отложим отрезок aa'. Через конец этого отрезка и начало координат проведем прямую, которая определит распределение скоростей для точек звена 1, лежащих на оси ri . Эта прямая образует с осью ri угол y1. Так как в точке c скорости звеньев 2 и 3 равны между собой и равны нулю, то, соединяя точку с прямой с точкой a, получим линию распределения скоростей для звена 2. Так как точка b принадлежит звеньям 2 и h, то ее скорость определяется по лучу сa' для радиуса, равного rB = (r1 + r2), что в масштабе mV , мм/мс-1 соответствует отрезку bb'. Соединяя точку b' с началом координат прямой, найдем линию распределения скоростей для водила. Эта линия образует с осью ri угол yh . Передаточное отношение планетарного механизма, определенное по данным графическим построениям, можно записать так:
 = w1 / wh = tgy1 / tgyh = aa' / aa".
= w1 / wh = tgy1 / tgyh = aa' / aa".

Рис. 4.3.23
Пример 3.Подбор чисел зубьев для планетарного механизма (рис. 4.3.24).
Условия, которые необходимо выполнить при подборе чисел зубьев колес типового планетарного механизма:
1. Заданное передаточное отношение с требуемой точностью.
 2. Соосность входного и выходного валов механизма.
2. Соосность входного и выходного валов механизма.
3. Свободное размещение (соседство) сателлитов.
4. Сборка механизма при выбранных числах зубьев колес.
5. Отсутствие подреза зубьев с внешним зацеплением.
6. Отсутствие заклинивания во внутреннем зацеплении.
7. Минимальные относительные габариты механизма.
По условию задачи дано u1k = 0,1, k = 3. Определить z1, z2, z3, z4.
Для решения этой задачи используем метод сомножителей. Зубья колес планетарного механизма, рассчитанные этим методом, удовлетворяют условиям 1, 2, 5 и 6. Проверяем эти зубья по условиям 3 (соседство) и 4 (сборка) и, если они выполняются, считаем этот вариант одним из возможных решений. Если после перебора рассматриваемых сочетаний сомножителей получим несколько возможных решений, то проводим их сравнение по условию 7. Решением задачи будет сочетание чисел зубьев, обеспечивающее габаритный минимальный размер R.
Передаточное отношение данного механизма:
u1h = 1 – z2z4 / z1z3;
–1 / 10 = 1 – z2z4 / z1z3;
z2z4 / z1z3 = BD / AC = 11 / 10;
11 / 10 = 1 × 11 / 2 × 5 = 11 × 1 / 5 × 2 = 11 × 1 / 2 × 5 = 1 × 11 / 5 × 2.
Условие соосности для этой схемы:
z1 + z2 = z3 + z4.
Выразим его через сомножители
a(A + B) = b(C + D).
Принимаем коэффициенты a = (D + C), b = (A + B) и получаем для первого сочетания сомножителей:
z1 = (D + C)Aq = (11 + 5)2q = 32q;
z2 = (D + C)Bq = (11 + 5)1q = 16q;
z3 = (A + B)Cq = (2 + 1)5q = 15q;
z4 = (A + B)D q = (2 + 1)11q = 33q,
при q = 2 z1 = 64, z2 = 32, z3 = 30, z4 = 66.
Проверка условия соседства:
sin(p / k) > max[(z2,3 +2 ) / (z1 + z2)];
0,866 > 0,375 – условие выполняется.
Проверка условия сборки:
(u1hz1 / k)(1 + kp) = B (целое число);
(–2 / 10 × 3)(1 + 3p) – не целое число, условие сборки не выполняется.
Следовательно, рассмотрим второе сочетание сомножителей:
z1 = (D + C)Aq = (1 + 2)5q = 15q;
z2 = (D + C)Bq = (1 + 2)11q = 33q;
z3 = (A + B)Cq = (5 + 11)2q = 32q;
z4 = (A + B)D q = (5 + 11)1q = 16q,
при q = 2 z1 = 30, z2 = 66, z3 = 64, z4 = 32.
Проверка условия соседства:
sin(p / k) > max[(z2,3 +2 ) / (z1 + z2)];
0,866 > 0,708 – условие выполняется.
Проверка условия сборки:
(u1hz1 / k)(1 + kp) = B (целое число);
(–30 / 10 × 3)(1 + 3p) = B – целое число, условие выполняется.
То есть получен первый вариант решения.
Габаритный размер:
R = min [max (z1 + 2z2)] = 81.
Рассмотрим третье сочетание сомножителей:
z1 = (D + C)Aq = (1 + 5)2q = 12q;
z2 = (D + C)Bq = (1 + 5)11q = 66q;
z3 = (A + B)Cq = (2 + 11)5q = 65q;
z4 = (A + B)Dq = (2 + 11)1q = 13q,
при q = 2 z1 = 24, z2 = 132, z3 = 130, z4 = 26.
Проверка условия соседства:
sin(p / k) > max[(z2,3 +2) / (z1 + z2)];
0,866 > 0,858 – условие выполняется.
Проверка условия сборки:
(u1hz1 / k)(1 + kp) = B (целое число)
(–24 / 10 × 3)(1 + 3p) – не целое число, условие не выполняется.
Рассмотрим последнее сочетание сомножителей:
z1 = (D + C)Aq = (11 + 2)5q = 65q;
z2 = (D + C)Bq = (11 + 2)1q = 13q;
z3 = (A + B)Cq = (5 + 1)2q = 12q;
z4 = (A + B)Dq = (5 + 1)11q = 66q,
при q = 2 z1 = 130, z2 = 26, z3 = 24, z4 = 132.
Проверка условия соседства:
sin(p / k) > max[(z2,3 +2 ) / (z1 + z2)];
0,866 > 0,179 – условие выполняется.
Проверка условия сборки
(u1hz1 / k)(1 + kp) = B (целое число);
(– 130 / 10 × 3)(1 + 3p) – не целое число, условие не выполняется.
Следовательно, только второе сочетание сомножителей удовлетворяет заданным условиям.
Ответ: z1 = 30, z2 = 66, z3 = 64, z4 = 32.
Тестовые задания по разделу «Теория механизмов и машин»
 1. Какая цепь изображена на рисунке?
1. Какая цепь изображена на рисунке?
а) простая замкнутая кинематическая цепь;
б) простая открытая кинематическая цепь;
в) сложная открытая кинематическая цепь;
г) сложная замкнутая кинематическая цепь.
 2. Укажите класс кинематической пары, изображенной на рисунке.
2. Укажите класс кинематической пары, изображенной на рисунке.
а) пара 1-го класса;
б) пара 2-го класса;
в) пара 3-го класса;
г) пара 4-го класса;
3. Как назвается звено 3 на схеме механизма называется?
 а) кривошип;
а) кривошип;
б) стойка;
в) шатун;
г) коромысло;
д) кулиса.
4. Какая кинематическая пара, изображена на рисунке?
 а) поступательная пара;
а) поступательная пара;
б) вращательная пара;
в) винтовая пара;
г) зубчатая пара.
5. Группы Ассура 2-го класса могут быть…
а) двух видов;
б) трех видов;
в) четырех видов;
г) пяти видов.
д) бесконечного множества видов.
6. Укажите класс кинематической пары, изображенной на рисунке.
 а) пара 1-го класса;
а) пара 1-го класса;
б) пара 2-го класса;
в) пара 3-го класса;
г) пара 4-го класса;
д) пара 5-го класса.
 7. Какая кинематическая пара изображена на рисунке?
7. Какая кинематическая пара изображена на рисунке?
а) поступательная пара;
б) вращательная пара;
в) винтовая пара;
г) зубчатая пара.
8. Какая цепь изображена на рисунке?
 а) простая замкнутая кинематическая цепь;
а) простая замкнутая кинематическая цепь;
б) простая открытая кинематическая цепь;
в) сложная открытая кинематическая цепь;
г) сложная замкнутая кинематическая цепь.
9. W = 3n – 2p5 – p4. Эта формула описывает:
а) момент сопротивления прямоугольника;
б) степень подвижности плоского механизма;
в) силу инерции при поступательном движении;
г) момент силы относительно оси.
 10. Укажите класс кинематической пары, изображенной на рисунке.
10. Укажите класс кинематической пары, изображенной на рисунке.
а) пара 1-го класса;
б) пара 2-го класса;
в) пара 3-го класса;
г) пара 4-го класса;
д) пара 5-го класса.
 11. Схема какого механизма изображена на рисунке?
11. Схема какого механизма изображена на рисунке?
а) кулисного механизма;
б) кривошипно-коромыслового механизма;
в) кривошипно-ползунного механизма;
г) двухкоромыслового механизма.
 12. Схема какого механизма изображена на рисунке?
12. Схема какого механизма изображена на рисунке?
а) кривошипно-ползунного механизма;
б) кулисного механизма;
в) кривошипно-коромыслового механизма;
г) двухкоромыслового механизма;
д) кулачкового механизма.
 13. Схема какого механизма изображена на рисунке?
13. Схема какого механизма изображена на рисунке?
а) кривошипно-ползунного механизма;
б) кулисного механизма;
в) кулачкового механизма;
г) кривошипно-коромыслового механизма;
д) двухкоромыслового механизма.
14. Схема какого механизма изображена на рисунке?
 а) кривошипно-ползунного механизма;
а) кривошипно-ползунного механизма;
б) кулачкового механизма;
в) механизма качающегося цилиндра;
г) кривошипно-коромыслового механизма;
д) двухкоромыслового механизма.
 15. Укажите класс кинематической пары, изображенной на рисунке.
15. Укажите класс кинематической пары, изображенной на рисунке.
а) пара 1-го класса;
б) пара 2-го класса;
в) пара 3-го класса;
г) пара 4-го класса;
д) пара 5-го класса.
 17. Какая цепь изображена на рисунке?
17. Какая цепь изображена на рисунке?
а) простая замкнутая кинематическая цепь;
б) простая открытая кинематическая цепь;
в) сложная открытая кинематическая цепь;
г) сложная замкнутая кинематическая цепь.
18. Коэффициент полезного действия – это …
а) отношение величины силы инерции звена к уравновешивающей силе;
б) отношение величины работы вредных сопротивлений к работе движущих сил;
в) отношение величины работы полезных сопротивлений к работе движущих сил;
г) отношение работы полезных сопротивлений к работе вредных сопротивлений.
19. Как называется звено 3 на схеме механизма ?
 а) кулиса;
а) кулиса;
б) стойка;
в) шатун;
г) коромысло;
д) ползун.
19. Что определяют методом Жуковского?
а) силу инерции;
б) уравновешивающую силу;
в) угловую скорость вращения;
г) степень подвижности механизма.
 20. Степень подвижности механизма, изображенного на рисунке, равна…
20. Степень подвижности механизма, изображенного на рисунке, равна…
а) W = 0;
2) W = 1;
3) W = 2;
4) W = 3.
21. Какую размерность имеет масштаб плана ускорений механизма?
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
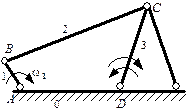 22. Чему равна степень подвижности механизма?
22. Чему равна степень подвижности механизма?
а) W = 0;
б) W = 1;
в) W = 2;
г) W = 3.
23. Группой Ассура называют…
а) группу рычажных механизмов;
б) кинематическую цепь, у которой степень подвижности W = 0;
в) кинематическую цепь, в которой содержатся только вращательные пары;
г) группу студентов с лозунгами и транспорантами.
24. В группе Ассура может содержаться…
а) только четное число подвижных звеньев;
б) только нечетное число подвижных звеньев;
в) любое число подвижных звеньев;
г) только два подвижных звена.
25. Укажите класс кинематической пары, изображенной на рисунке.
 а) пара 1-го класса;
а) пара 1-го класса;
б) пара 2-го класса;
в) пара 3-го класса;
г) пара 4-го класса;
д) пара 5-го класса.
26. В группе Ассура может содержаться…
а) только четное число кинематических пар 5-го класса;
б) только нечетное число кинематических пар 5-го класса;
в) любое число кинематических пар 5-го класса;
г) число пар 5-го класса, в 1,5 раза больше числа подвижных звеньев.
 27. Как называется звено 2 на схеме механизма?
27. Как называется звено 2 на схеме механизма?
а) ползун;
б) кривошип;
в) кулисный камень;
г) коромысло;
д) шатун.
28. В состав плоского механизма могут входить…
а) только кинематические пары 1-го, 2-го, 3-го класса;
б) только кинематические пары 4-го и 5-го класса;
в) кинематические пары любого класса.
29. Какую размерность имеет масштаб плана скоростей механизма?
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
30. Как назвается звено 1 на схеме механизма, изображенного на рисунке?
 а) ползун;
а) ползун;
б) кривошип;
в) шатун;
г) коромысло;
д) кулиса.
31. Какую размерность имеет масштаб плана скоростей механизма?
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
32. Какой из видов зубчатого зацепления наиболее распространен в машиностроении?
а) эвольвентное зацепление.
б) циклоидальное зацепление.
в) круговинтовое зацепление.
 |
33. Какой из планов скоростей соответствует данному положению механизма?
34. При решении динамических задач в ТММ используют…
а) принцип Паули;
б) принцип домино;
в) принцип Даламбера;
г) формулу Эйлера.
 35. Как называется звено 3 на схеме механизма, изображенного на рисунке?
35. Как называется звено 3 на схеме механизма, изображенного на рисунке?
а) ползун;
б) кривошип;
в) кулиса;
г) коромысло;
д) шатун.
36. Маховик устанавливают с целью …
а) увеличить скорость механизма;
б) уменьшить скорость механизма;
в) уменьшить неравномерность движения;
 г) увеличить вес механизма.
г) увеличить вес механизма.
37. Как называется звено 3 на схеме механизма, изображенной на рисунке?
а) ползун;
б) стойка;
в) кулиса;
г) коромысло;
д) шатун.
38. Диаграмму энергомасс используют для определения…
а) энергии звеньев механизма;
б) масс звеньев механизма;
в) момента инерции маховика;
г) величины уравновешивающей силы.
39. Ползун на плоскости придет в движение, если направление действующей на него силы …
а) лежит вне конуса трения;
б) лежит внутри конуса трения;
в) перпендикулярно направлению движения.
Дата добавления: 2014-11-13; просмотров: 797; Мы поможем в написании вашей работы!; Нарушение авторских прав |