Потери на трение по длине

При равномерном движении жидкости в трубах постоянного диаметра потери напора на трение по длине трубы, как для ламинарного, так и для турбулентного течения, определяются по формуле Дарси-Вейсбаха: ,

где h, м - потери напора; λ - безразмерный коэффициент гидравлического трения;

l, м - длина трубы; d, м- внутренний диаметр трубы; ν, м/с - средняя скорость в сечении потока.

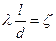, или λ = при l = d, т.е. коэффициент гидравлического трения представляет собой коэффициент сопротивления трубопровода длиной, равной внутреннему диаметру трубы.

В чем состоит физический смысл коэффициента трения λ?

Рассмотрим равновесие столбика жидкости длиной l и радиусом r.

Сила давления F = (p₁ – p₂) pr²; сила трения R = t 2prl,

где pr² – площадь живого сечения столбика жидкости; 2prl – площадь боковой поверхности столбика.

(p₁ – p₂) pr² = t 2prl, отсюда Dр_тр. = (p₁ – p₂) = .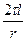

Потери удельной энергии на трение в давлениях составляют: Dр_тр. = ρgλ , тогда 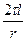= ρgλ , отсюда λ = .

Физический смысл коэффициента гидравлического трения заключается в пропорциональности касательному напряжению, отнесенному к динамическому давлению.

В общем случае коэффициент λ зависит от относительной шероховатости внутренней поверхности стенок труб и числа Рейнольдса: l = f (Re, D/d),

где D/d - относительная шероховатость трубы; D - абсолютная эквивалентная шероховатость трубы. Ее можно представить в виде песчинок одинакового размера, потери на которых эквивалентны потерям при реальной шероховатости трубы:

Величина абсолютной эквивалентной шероховатости трубы Δ выбирается по справочникам с учётом материала, способа изготовления, срока службы и условий эксплуатации трубы.

Зависимость λ = f (Re; Δ/d) можно рассмотреть на графике Мурина.

Рис. График Мурина

В зависимости от режима течения эту зависимость можно разбить на две зоны:

1) зону ламинарного течения (Re ≤ 2320), где шероховатость не влияет нa сопротивление, коэффициент λ зависит только от числа Рейнольдса и определяется по формуле Пуазейля: ;

2) зону турбулентного течения (Re >2320). Для расчета величины коэффициента λ существует ряд эмпирических формул, одной из которых явля­ется универсальная формула Альтшуля: .

В зависимости от соотношения и зону турбулентного течения можно разбить на три области, отличающиеся характером изменения ко­эффициента λ:

а) область гидравлически гладких труб, где >> (при относительно небольших значениях чисел Re и малой шероховатости стенок труб), когда λ не зависит от шероховатости и определяется лишь числом Рейнольдса.

В этом случае коэффициент λ может быть вычислен по формуле Блазиуса: ;

б) переходная область, где и соразмерны, когда коэффициент λ зависит одновременно от двух параметров - числа Re и относительной ше­роховатости, и может быть вычислен по формуле Альтшуля;

в) область гидравлически шероховатых труб, где << (при очень больших значениях чисел Re), когда коэффициент λ нe зависит от числа Re, а определяется лишь относительной шероховатостью.

Коэффициент λ можно вычислить по формуле Шифринсона: .

Эта область еще носит название область квадратичного сопротивления, так как потери напора пропорциональны скорости (расходу) во второй степе­ни, или область автомодельности по числу Рейнольдса, т.е. коэффициент λ не зависит от числа Рейнольдса.

Разделение зоны турбулентного течения на области гидравлическо­го сопротивления физически можно объяснить следующим образом.

В турбулентном потоке непосредственно у стенки трубы имеется ламинарный подслой, толщина которого зависит от числа Re и может быть приближенно определена пo формуле: .

Из этой формулы видно, что с увеличением скорости движения жидкости в трубе (соответственно числа Re) толщина ламинарного подслоя уменьшается.

В зависимости от соотношения эквивалентной абсолютной шерохова­тости трубы Δ и толщины ламинарного подслоя δ_л различают трубы гид­равлически гладкие и гидравлически шероховатые.

Если δ_л >Δ, поток не испытывает дополнительных завихрений от ше­роховатости поверхности. Такая труба называется гидравлически гладкой.

Если же δ_л<Δ, выступы шероховатости оголяются и в обтекающую их жидкость вносят дополнительные возмущения. В этом случае труба назы­вается гидравлически шероховатой.

а) - гидравлически гладкая труба; б) – труба работающая в переходной области со­противления;

в) - гидравлически шероховатая труба.