Равномерное вращение сосуда с жидкостью вокруг вертикальной оси

Сосуд с жидкостью вращается с угловой скоростью ω = const.

Ha жидкость действуют две единичные массовые силы: сила тяжести g и сила инерции а = ω² r.

Равнодействующая 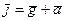и направлена по нормали к поверхности жидкости.

жидкости. tg tga = = ; тогда dz = dr.

Интегрируя это выражение, получаем: z = + с.

Для начальных условий r = 0 с = z_о, окончательно

z = +z_o - уравнение свободной поверхности жид­кости, параболоид вращения, вершина которого находится на расстоянии z_o от дна сосуда.

Определим зависимость давления в произвольной точке жидкости как функцию от r и z.

Условие равновесия столбика жидкости площадью ds в проекции на ось Oz:

pds – (z_o – z_М + )ρgds = 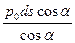, где cosα = .

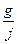Сокращая на ds, получаем: р = p_o + + ρg(z_о- z_M) - давление во вращающейся жидкости. Оно возрастает пропорционально радиусу r и уменьшается пропорционально высоте z_M.