Плоскость сравнения. Пьезометр

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность - одна из них (h = 0).

Плоскость, от которой отсчитываются координаты сечений, называется плоскостью сравнения. Возьмем на произвольной высоте плоскость сравнения:

z - координата точки М; z_о- координата свободной поверхности.

Заменив в основном уравнении гидростатики h = z_о- z, получаем:

р = р_о + ρg(z_о - z); p = р_о + ρgz_о - ρgz; z + p/ρg = z_о + р_о/ρg.

Можно утверждать, что z + р/ρg = const. Координата z называется геометрической высотой, величина р/ρg - пьезометрической высотой, а (z + р/ρg) - гидростатическим напором. Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости

При определении гидростатического давления, как правило, оперируют избыточным давлением или вакуумом, т.к. атмосферное давление действует со всех сторон, то его можно нe принимать во внимание.

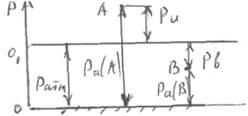
Избыточное давление в жидкости можно определить пo пьезометру. Пьезометр - это тонкая прозрачная трубка, прикрепленная к небольшому отверстию в стенке трубы или сосуда. Плос­кость атмосферного давления, горизонтальная плоскость, проходящая через уровень жидкости в пьезометре, называется пьезометрической плоскостью. Если сосуд открыт в атмосферу, то пье­зометрическая плоскость совпадает со свободной поверхностью жидкости.

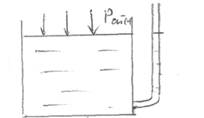
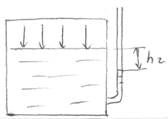
h – пьезометрическая высота;

h = 0; h₁ =р_и/ρg; h₂ =р_в/ρg.