Определение продольного перемещения свободного конца трубы на участке подземного трубопровода.

Рассмотрим прямолинейный подземный участок трубопровода, правый конец которого будем считать неподвижным (рисунок 33). Полагается, что длина участка ограничена и равна .

Рисунок 33. Расчетная схема подземного участка магистрального трубопровода.

Расчетная модель магистрального трубопровода представляет собой стержень кольцевого сечения, взаимодействующий со средой, которая моделирует работу реального грунта.

Предполагается, что взаимодействие трубы со средой происходит в соответствии с идеализированной диаграммой зависимости распределенной продольной нагрузки от продольных перемещений (рисунок 34), которая построена на основании диаграммы (рисунок 32).

Для того, чтобы определить погонную осевую силу сопротивления грунта, достаточно умножить касательные напряжения , равномерно распределенные по поверхности трубы, на периметр трубы

, (9.12)

и с учетом (9.11)

. (9.13)

Рисунок 34. Диаграмма продольных нагрузок

Аналитически модель грунта описывается двумя участками:

· участок линейноупругой связи между трубой и грунтом

при ; (9.14)

· участок пластической связи между трубой и грунтом

при . (9.15)

Участок, где при взаимодействии трубопровода с грунтом , называется участком предельного равновесия, его длина равна (первый участок I на рисунке 33).

На основании анализа результатов проведенных экспериментов для определения предельного сопротивления грунта сдвигу рекомендуется следующая формула:

, (9.16)

где – вес трубопровода с продуктом;

– угол внутреннего трения грунта;

– объемный вес грунта;

– безразмерный коэффициент, учитывающий образование свода обрушения;

– коэффициент сцепления грунта, МПа (характеристика грунта, зависит от коэффициента пористости).

Коэффициента образования свода обрушения можно определить по диаграмме (рисунок 35) или с помощью рекомендуемых эмпирических формул

· для песчаного грунта (9.17)

· для глинистых грунтов . (9.18)

Рисунок 35. Коэффициент образования свода обрушения.

1 – песчаный грунт; 2 – глинистый грунт.

В зависимости от нагрузок и относительной жесткости трубопровода возможны два варианта его работы:

· имеется один участок; отсутствует участок предельного равновесия грунта; между трубой и грунтом существует только упругая связь; ;

· имеются два участка работы; существует участок предельного равновесия грунта; на первом участке взаимодействие между трубой и грунтом упругое; на втором пластическое.

Для вычисления продольных деформаций необходимо учитывать температурные воздействия и нагрузки от внутреннего давления

, (9.19)

где 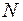– продольная сила в поперечных сечениях трубы;

– модуль упругости материала трубы;

– площадь кольцевого сечения трубы;

– коэффициент линейного расширения материала трубы;

– температурный перепад положительный при нагреве;

– коэффициент Пуассона;

– кольцевые напряжения.

Из полученного выражения (9.14) получаем формулу для определения продольной силы

(9.20)

С учетом соотношения Коши

. (9.21)

Если ввести обозначение

, (9.22)

то уравнение для продольной силы будет записано в следующем виде

(9.23)

С учетом уравнения равновесия (9.2) получаются выражения для продольных перемещений W

· на первом участке

или (9.24)

· на втором участке

(9.25)

где . (9.26) Таким образом, для определения перемещений поперечных сечений трубопровода получены дифференциальные однородные уравнения второго порядка с постоянными коэффициентами (9.17) и (9.18).

Для получения решения первого дифференциального уравнения проводим дважды интегрирование

(9.27)

с учетом получается выражение для продольной силы на первом участке

, (9.28)

где – постоянные интегрирования.

Если в полученные уравнения подставить координату , то получим перемещение и продольную силу в начале трубы (свободного конца трубы)

, (9.29)

. (9.30)

Из выражения (9.25) определим постоянную интегрирования

(9.31)

Для второго дифференциального уравнения (9.20) необходимо составить характеристическое уравнение

, (9.32)

корни которого позволяют получить решение для продольных перемещений на втором участке трубопровода

(9.33)

где - гиперболический косинус;

- гиперболический синус для аргумента .

Рисунок 35. Графики гиперболических функций.

С учетом получаем уравнение для продольной силы

, (9.34)

где – постоянные интегрирования.

Если в уравнение (9.27) подставить условие при , , то получим

, откуда

, (9.35)

где - гиперболический тангенс .

Для решения практических задач необходимо определить постоянные и длину участка предельного равновесия трубопровода . С этой целью сформулируем граничные условия, кроме тех которые уже были использованы.

При продольные перемещения на конце первого участка и в начале второго равны , также как и продольные силы , кроме того, в этом сечении продольное перемещение становится равным предельному .

После реализации всех условий получаем

;

; (9.36)

; (9.37)

(9.38)

Величина определяется, в результате решения трансцендентного уравнения (9.32).

После определения вычисляются произвольные постоянные , которые позволяют определить .

Также определяются продольное перемещение в начале участка трубопровода и продольное усилие в конце участка

. (9.39)

Однако следует отметить, что для получения полного решения задачи об определении продольных перемещений подземного трубопровода ещё не известна длина участка трубопровода , на которой продольные перемещения станут равны нулю. При рассмотрении конкретных задач, как правило, удается решить эту проблему.

Далее рассмотрены частные случаи подземных трубопроводов. Один из наиболее распространенных случаев, когда можно считать участок трубопровода полубесконечным, т.е. длина участка трубопровода стремится к бесконечности, а гиперболический тангенс стремится к единице в соответствии с графиком (рисунок 35)

;

Это условие позволяет определить длину участка предельного равновесия из выражения (9.32)

(9.40)

С учетом полученного выражения для , из уравнений (9.26), (9.29), (9.30), (9.31) находим постоянные интегрирования

(9.41)

(9.42)

. (9.43)

Перемещения в начале участка получается из уравнения (9.24)

(9.44)

Усилия в защемленной части трубопровода, где продольные перемещения , определяются из уравнения (9.33) при условии, что гиперболический косинус стремится к бесконечности

,

. (9.45)

Для того, чтобы оценить длину участка магистрального трубопровода необходимо ввести критерий, который будет устанавливать, когда размер участка можно считать бесконечно длинным.

Для решения практических задач достаточную точность будет обеспечивать следующее условие: перемещение правого конца участка равняется 0,01 от перемещения сечения, соответствующего концу участка предельного равновесия.

, (9.46)

где

Из уравнения (9.27) с учетом (9.29)

.

Для , (рисунок 35)

. (9.47)

С учетом определения гиперболических функций

(9.48)

Подставляем (9.42) в (9.41) с учетом (9.37)

и после сокращений

или .

. (9.49)

Подставив вместо его значение из (9.34) и вычислив логарифм получаем окончательное выражение

. (9.50)

Однако, нужно не забывать, что полученные решения относятся к варианту, когда по длине трубопровода имеются два участка взаимодействия трубы и грунта, т.е. существует участок предельного равновесия грунта. Поэтому, чтобы выбрать правильный вариант решения, нужно иметь критерий наличия участка предельного равновесия грунта. Анализируя выражение (9.32), определим условие, когда .

Если , то и . С учетом этого легко получить критерий для существования участка предельного равновесия грунта

. (9.51)

Если можно считать трубопровод полубесконечным

при , условие (9.45) упрощается

. (9.52)