
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Некоторые случаи вычисления работы.
1) Работа сил тяжести, действующих на систему. Работа силы тяжести, действующей на частицу весом  , будет равна
, будет равна 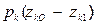 , где
, где 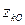 и
и  - координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна
- координаты, определяющие начальное и конечное положение частицы. Тогда сумма работ всех сил тяжести, действующих на систему, будет равна
 ,
,
где Р - вес системы,  - вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей Р на перемещении центра тяжести (или центра масс) системы.
- вертикальное перемещение центра тяжести (или центра масс). Следовательно, работа сил тяжести, действующих на систему, вычисляется как работа их равнодействующей Р на перемещении центра тяжести (или центра масс) системы.
2) Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.27) будет равна
 ,
,
так как  , где
, где 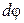 - угол поворота тела.
- угол поворота тела.
Но, как легко видеть,  . Будем называть величину
. Будем называть величину  вращающим моментом. Тогда получим:
вращающим моментом. Тогда получим:  .
.
Следовательно, в рассматриваемом случае элементарная работа равна произведению вращающего момента на элементарный угол поворота. Формула справедлива и при действии нескольких сил, если считать  .
.
 При повороте на конечный угол
При повороте на конечный угол  работа будет равна
работа будет равна
 ,
,
а в случае постоянного момента 
 .
.
|
Укажем еще, как в данном случае определяется мощность
 .
.
Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощности вращающий момент будет тем больше, чем меньше угловая скорость.
 3) Работа сил трения, действующих на катящееся тело. На колесо радиуса R (рис.28), катящееся по некоторой плоскости (поверхности) без скольжения, действует сила трения F , препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы
3) Работа сил трения, действующих на катящееся тело. На колесо радиуса R (рис.28), катящееся по некоторой плоскости (поверхности) без скольжения, действует сила трения F , препятствующая скольжению точки касания В вдоль плоскости. Элементарная работа этой силы  . Но точка В в данном случае является мгновенным центром скоростей и
. Но точка В в данном случае является мгновенным центром скоростей и  . Так как
. Так как 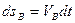 , то
, то  и для каждого элементарного перемещения
и для каждого элементарного перемещения  .
.
Следовательно, при качении без скольжения, работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю. По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.28,а).
Сопротивление качению, возникающее вследствие деформации поверхностей (pис.28,б), создает пару (  ), момент которой
), момент которой  , где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса
, где k- коэффициент трения качения. Тогда учитывая, что при качении угол поворота колеса  , получим:
, получим:
 ,
,
где  - элементарное перемещение центра С колеса.
- элементарное перемещение центра С колеса.
Если N= const, то полная работа сил сопротивления качению будет равна

Так как величина  /R мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.
/R мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.
Дата добавления: 2014-12-23; просмотров: 287; Мы поможем в написании вашей работы!; Нарушение авторских прав |