
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
С помощью ППП Ехсеl. Здесь на примерах будут показаны возможности ППП Ехсеl при синтезе моделей временных рядов.
Здесь на примерах будут показаны возможности ППП Ехсеl при синтезе моделей временных рядов.
Пример 5.1. В табл. 5.3 приведены данные, отражающие спрос на некоторый товар за восьмилетний период (усл.ед.).
Таблица 5.3
| Год, t | ||||||||
| Спрос, уt |
Необходимо создать адекватную модель временного ряда и оценить прогноз индивидуального значения спроса на товар на момент t = 9 (девятый год) с надежностью 0,95.
Предварительный анализ данных.
1. Выявление аномальных наблюдений. Из графика (рис. 5.1) видно, что под «подозрение», в смысле аномальности, попадает второй уровень (по отношению к третьему уровню).
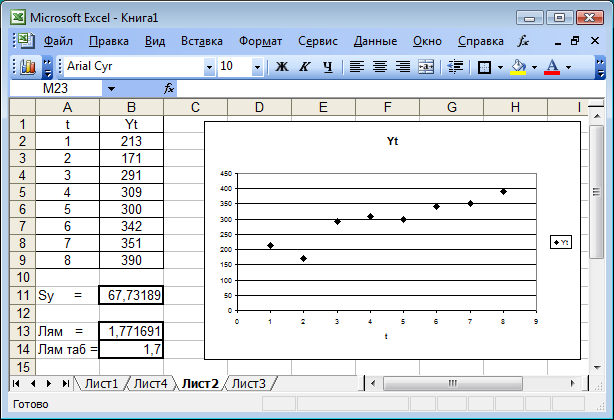
Рис. 5.1
Проверка с помощью критерия Ирвина (5.3) показала, что этот уровень действительно является аномальным, т.к. 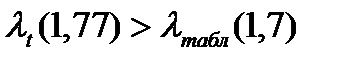 . Для вычисления Sy была использована функция СТАНДОТКЛОНП. Поэтому этот уровень заменяется средним значением соседних уровней (первого и третьего), т.е. принимается у3 = 252.
. Для вычисления Sy была использована функция СТАНДОТКЛОНП. Поэтому этот уровень заменяется средним значением соседних уровней (первого и третьего), т.е. принимается у3 = 252.
2. Проверка наличия тренда. Для реализации алгоритма разности средних уровней временную последовательность разбиваем на две части по 4 уровня в каждой.
Гипотезу о равенстве дисперсий проверим с помощью F-теста, который можно найти среди инструментов Анализа данных(рис.5.2).
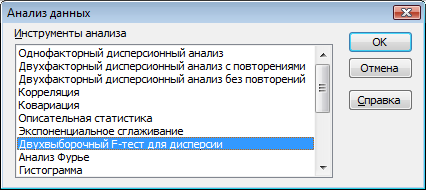
Рис. 5.2
Вводим данные для выполнения F-теста, указывая интервал для первой и второй переменных (рис. 5.3). Результат выполнения теста приведен на рис. 5.4. Анализируя результаты выполнения двухвыборочного F-теста для проверки гипотезы о равенстве дисперсий, приходим к выводу, что выборочные дисперсии ( 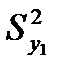 и
и 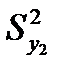 ) различаются незначительно: Fнабл (1,34) < Fкр(9,28).
) различаются незначительно: Fнабл (1,34) < Fкр(9,28).
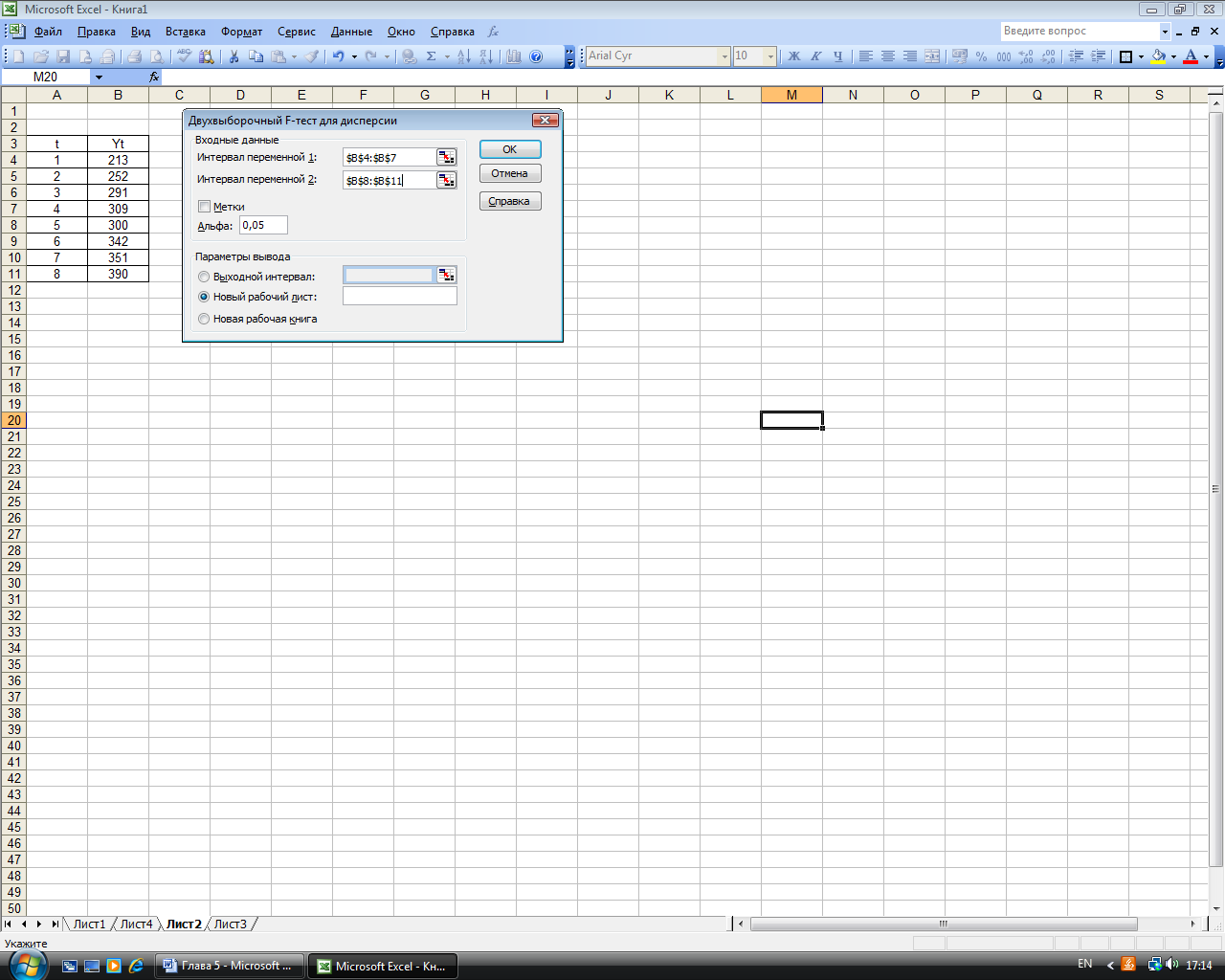
Рис. 5.3
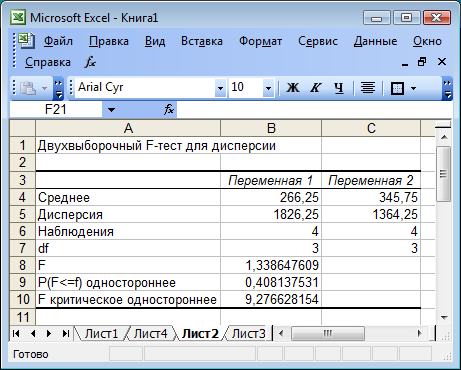
Рис. 5.4
При использовании процедуры «Двухвыборочный F-тест для дисперсии» следует иметь ввиду, что если Fнабл > 1, то Fкр = 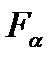 и рассматривается правосторонняя критическая область. При этом в качестве альтернативной гипотезы рассматривается гипотеза Н1 :
и рассматривается правосторонняя критическая область. При этом в качестве альтернативной гипотезы рассматривается гипотеза Н1 : 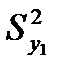 >
> 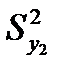 , т.е. различие дисперсий утверждается при Fнабл > Fкр. Если же Fнабл < 1, то Fкр =
, т.е. различие дисперсий утверждается при Fнабл > Fкр. Если же Fнабл < 1, то Fкр =  и рассматривается левосторонняя альтернативная гипотеза: Н1 :
и рассматривается левосторонняя альтернативная гипотеза: Н1 : 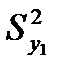 <
< 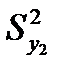 , при этом дисперсии выборок различаются, если Fнабл < Fкр.
, при этом дисперсии выборок различаются, если Fнабл < Fкр.
Проверка гипотезы о равенстве средних этих подвыборок осуществляется с помощью t – статистики Стьюдента (5.5). Для чего можно воспользоваться инструментом Анализа данных: Двухвыборочный t-тест с одинаковыми дисперсиями (рис. 5.5). Вводим данные. Результат выполнения t-теста приведен на рис. 5.6. Так как  , то делаем вывод о том, что тренд присутствует.
, то делаем вывод о том, что тренд присутствует.
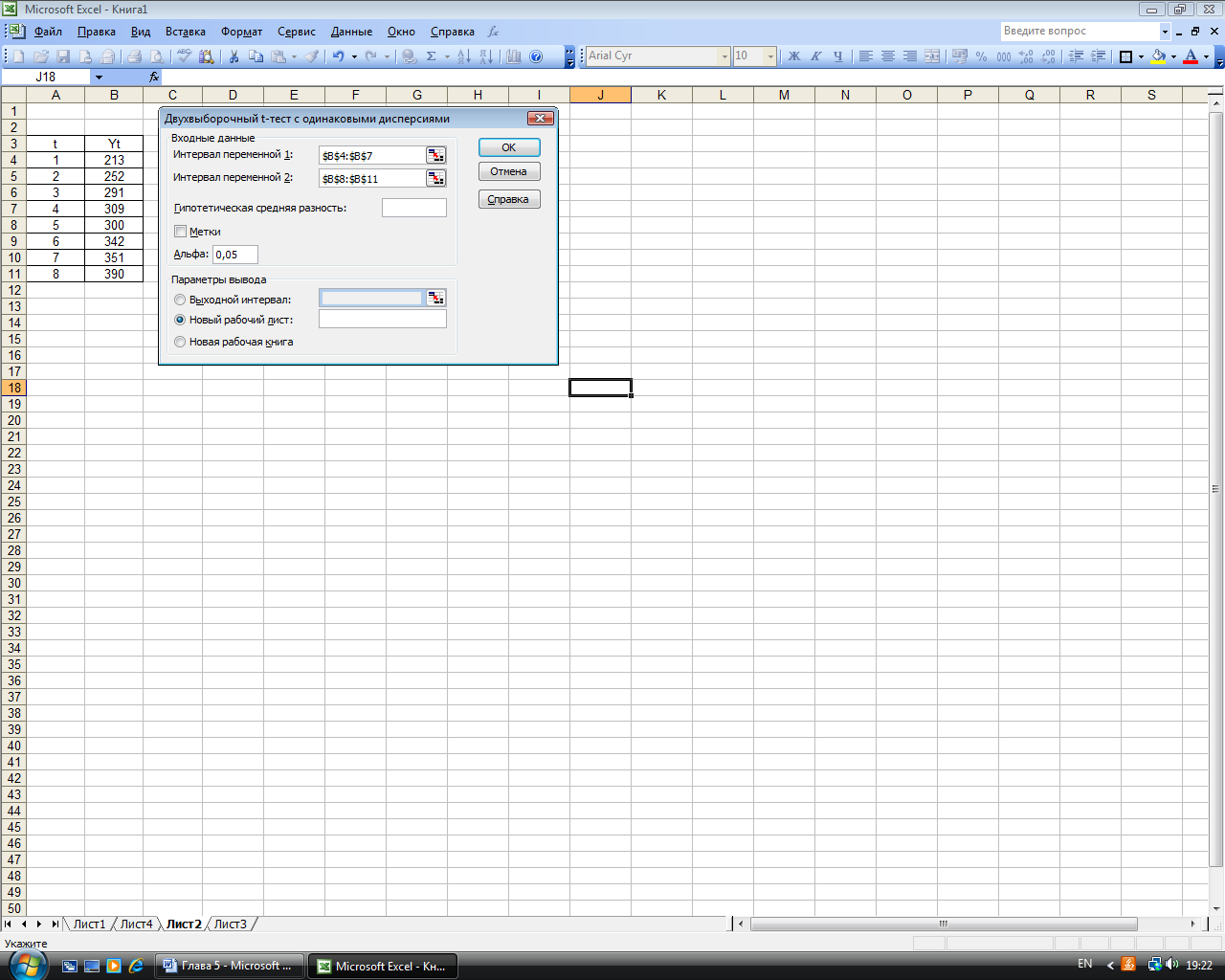
Рис. 5.5

Рис. 5.6
В качестве подтверждения наличия тенденции можно воспользоваться коррелограммой (рис. 5.7). Так как наиболее высоким оказался коэффициент автокорреляции первого порядка, то временной ряд содержит тенденцию. Кроме того с увеличением лага корреляция монотонно убывает, что свидетельствует о стационарности ряда, вероятностные свойства которого не изменяются во времени. Коэффициенты автокорреляции были получены с помощью статистической функции КОРРЕЛ.
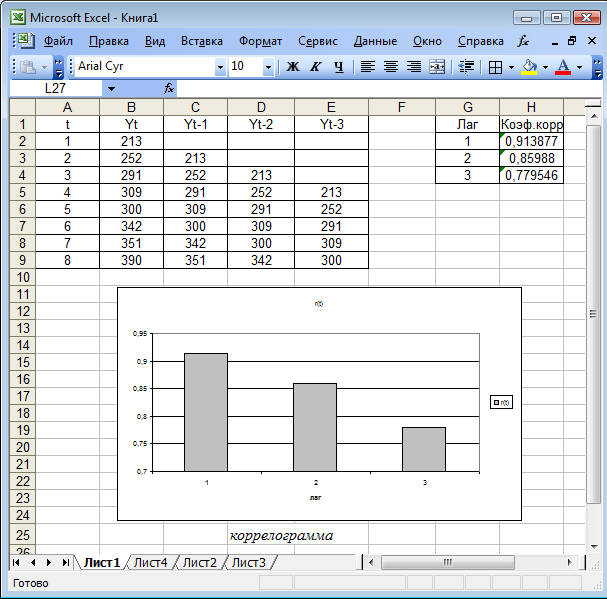
Рис. 5.7
3. Сглаживание временных рядов. К ряду вначале применим механическое сглаживание, а затем, для удобства прогноза, аппроксимируем его аналитически.
Для механического сглаживания применим метод простой скользящей средней с интервалом сглаживания m = 3 года. Результаты сглаживания представлены на рис. 5.8.
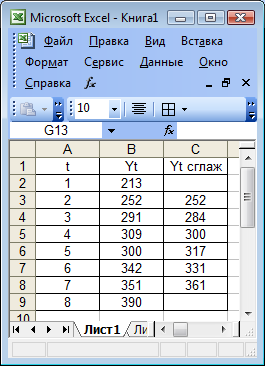
Рис. 5.8
Из графика сглаженного ряда видно, что наиболее подходящим трендом является линейный тренд. Уравнение линейного тренда, полученного с помощью функции ЛИНЕЙН (рис. 5.9), имеет вид
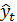
 .
.
Высокий коэффициент детерминации R2 = 0,98 и его статистическая значимость (F(211,7) > Fкр(7,7)) свидетельствуют о высоком качестве уравнения тренда.

Рис. 5.9
На рис. 5.9 также представлено прогнозное значение спроса на товар на 9–й год и его доверительный интервал, который был получен по формуле (5.15).
Пример 5.2. Имеются условные данные об объемах потребления электроэнергии (млн кВт ч) жителями региона за 16 кварталов (табл. 5.4).
Таблица 5.4
| t | ||||||||||||||||
| yt | 6,0 | 4,4 | 5,0 | 9,0 | 7,2 | 4,8 | 6,0 | 10,0 | 8,0 | 5,6 | 6,4 | 11,0 | 9,0 | 6,6 | 7,0 | 10,8 |
Необходимо синтезировать математическую модель и определить прогноз потребления электроэнергии в течение первого полугодия ближайшего следующего года. Нанесем эти значения на график (рис. 5.10).
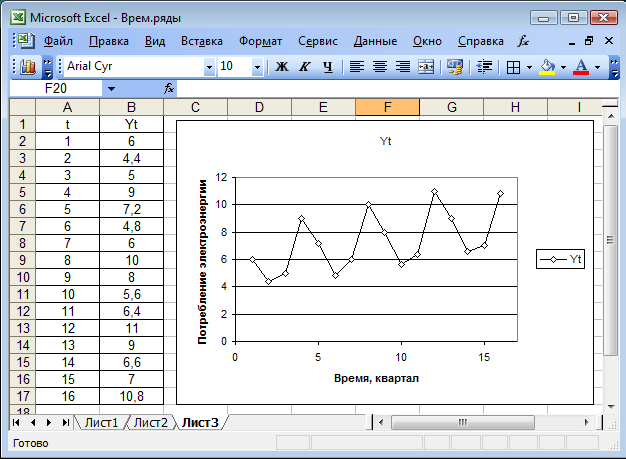
Рис. 5.10
Из графика рис. 5.10 видно, что во временном ряду присутствует сезонная составляющая и есть тенденция увеличения расхода. Подтвердим эти предварительные выводы статистическими методами.
Для этого построим коррелограмму (рис. 5.11). Построение было выполнено на компьютере по аналогии примера 5.1.

Рис. 5.11
Из коррелограммы рис. 5.11 видно, что самым высоким оказался коэффициент автокорреляции четвертого порядка, что свидетельствует о наличии сезонных колебаний с периодом равным 4. Подтверждением этого является значение r8. Кроме того значимыми являются r2 и r6 , что подтверждает наличие во временном ряду линейной тенденции.
По графику (рис. 5.10) можно установить наличие приблизительно равной амплитуды колебаний, что свидетельствует о возможной аддитивной модели этого ряда.
Построение аддитивной модели
Шаг 1. Проведем выравнивание исходных уровней ряда методом простой скользящей средней. Длина интервала сглаживания должна быть равна периоду колебаний, т.е. m = 4. В этом случае в формуле скользящей средней будут использоваться пять уровней с весовыми коэффициентами: 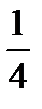 (1/2, 1, 1, 1, 1/2) (см.п. 5.1.2), т.е. первое сглаженное значение будет для третьего уровня, второе для четвертого и т.д.
(1/2, 1, 1, 1, 1/2) (см.п. 5.1.2), т.е. первое сглаженное значение будет для третьего уровня, второе для четвертого и т.д.

Рис. 5.12
Шаг 2. Найдем оценки сезонной компоненты (4 столбец табл. рис. 5.12), как разность между фактическими уровнями ряда yt (2 столбец) и центрированными скользящими средними (3 столбец).
Используем эти оценки для расчета сезонной компоненты S (рис. 5.13). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Si . Обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Для данной модели имеем 0,6 – 1,958 – 1,275 + 2,708 = 0,075. Определим корректирующий коэффициент k = 0,075/4 = 0,01875.
Скорректированное значение сезонной компоненты (последняя строка рис. 5.13) вычисляется по формуле 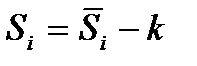 , i = 1, 2, 3, 4.
, i = 1, 2, 3, 4.
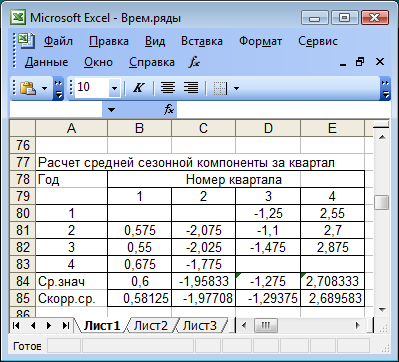
Рис. 5.13
Шаг 3. Вычтем сезонные компоненты из каждого уровня временного ряда, получим F + E = Y – S (4 столбец рис. 5.14).
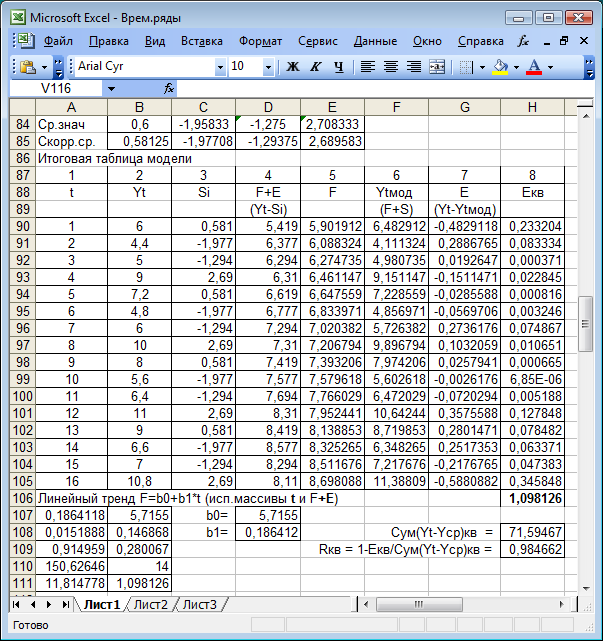
Рис. 5.14
Шаг 4. Определим компоненту F. Для этого по значениям F + E рассчитаем линейный тренд с использованием функции ЛИНЕЙН: 
 . Подставляя в это уравнение t = 1, 2, … получим 5 столбец.
. Подставляя в это уравнение t = 1, 2, … получим 5 столбец.
Шаг 5. Найдем значения уровней ряда, полученных по аддитивной модели. Для этого прибавим к уровням F их сезонные составляющие Yt мод = F + S (6 столбец).
Шаг 6. Найдем ошибки (7 столбец). Из рис. 5.14 следует, что коэффициент детерминации R2 = 0,985. Это свидетельствует о высоком качестве аддитивной модели, т.е. 98,5% общей вариации уровней временного ряда объясняется этой моделью.
Спрогнозируем потребление электроэнергии в течение первого полугодия следующего ( пятого) года, т.е. необходимо найти Y(17) + Y(18)
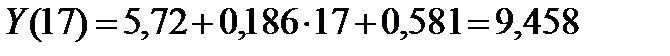 ;
;
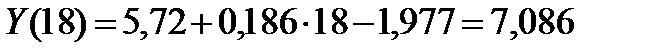 .
.
Таким образом, прогноз на следующее полугодие составит
(9,458 + 7,086) = 16,544 млн кВт ч.
Пример 5.3. Задачу примера 5.2 решим с использованием фиктивных переменных.
Модель будет иметь вид
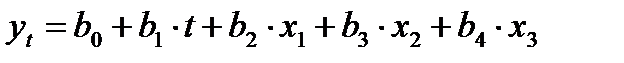 , (5.17)
, (5.17)
где 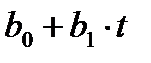 - линейный тренд; х1, х2, х3 – фиктивные переменные.
- линейный тренд; х1, х2, х3 – фиктивные переменные.
Фиктивные переменные принимают следующие значения:
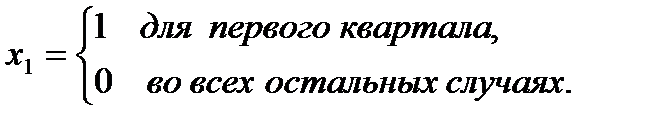
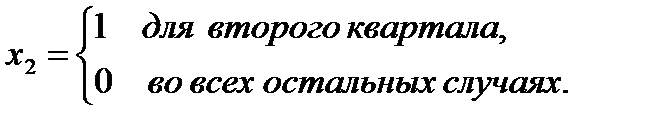
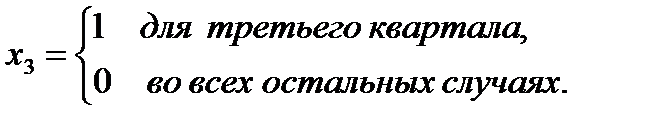
Результаты оценивания уравнения множественной регрессии (5.17) МНК представлены на рис. 5.15. Для определения коэффициентов была использована функция ЛИНЕЙН. Из рис. 5.15 видно, что адекватность модели статистическим данным достаточно высокая. Подтверждением высокого качества модели также является близость коэффициента детерминации R2 к единице (R2 = 0,985). Кроме того, все коэффициенты статистически значимы.
Пример 5.4. Поквартальные данные о прибыли компании (тыс. у.е.) представлены в табл. 5.5.
Таблица 5.5
| Год | Квартал | |||
| I | II | III | IV | |
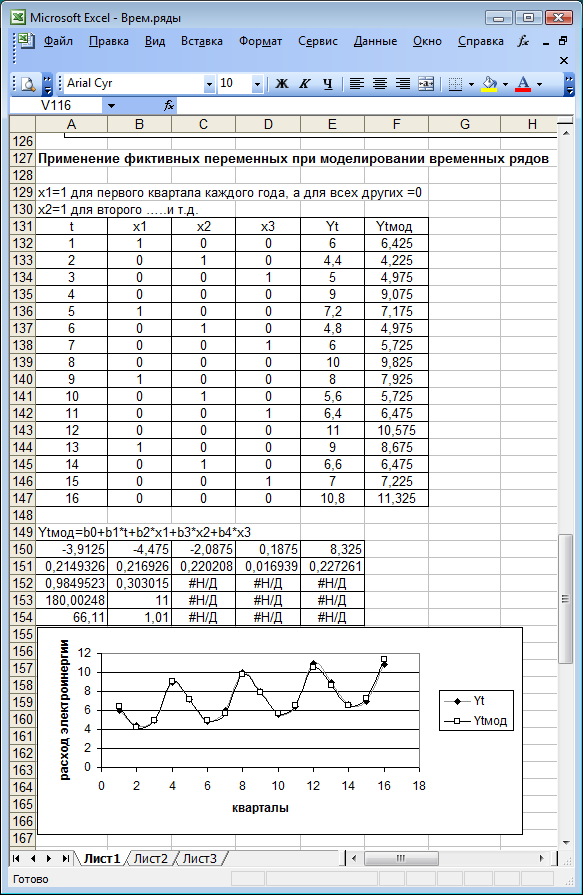
Рис. 5.15
Из графика (рис. 5.16) видно, что ряд имеет сезонные колебания (период равен 4) и общую убывающую тенденцию. Причем амплитуда колебаний также уменьшается. Это свидетельствует о том, что здесь необходимо использовать мультипликативную модель:  .
.
Рис. 5.16
Построение мультипликативной модели
Шаг 1. Выравнивание исходных уровней ряда методом простой скользящей средней. Этот шаг полностью совпадает с шагом 1 в аддитивной модели. Результаты выравнивания представлены на рис. 5.17.
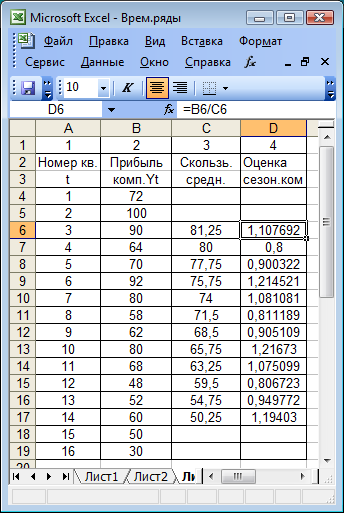
Рис. 5.17
Шаг 2. Оценка сезонной компоненты (4 столбец рис. 5.17), как отношение значений фактических уровней ряда yt (2 столбец) и центрированных скользящих средних (3 столбец). Средние квартальные значения сезонной компоненты 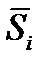 представлены на рис. 5.18.
представлены на рис. 5.18.
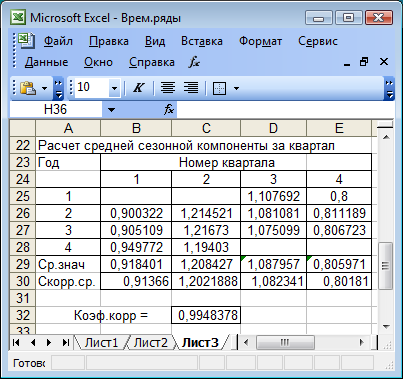
Рис. 5.18
Для определения корректирующего коэффициента воспользуемся соотношением k = 4/  = 0,9948. Скорректированные значения сезонной компоненты (последняя строка рис. 5.18) были получены по формуле
= 0,9948. Скорректированные значения сезонной компоненты (последняя строка рис. 5.18) были получены по формуле 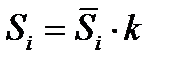 , i = 1, 2, 3, 4.
, i = 1, 2, 3, 4.
Шаг 3. Удалим сезонную компоненту из ряда 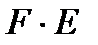 = Y / S (4 столбец рис. 5.19).
= Y / S (4 столбец рис. 5.19).
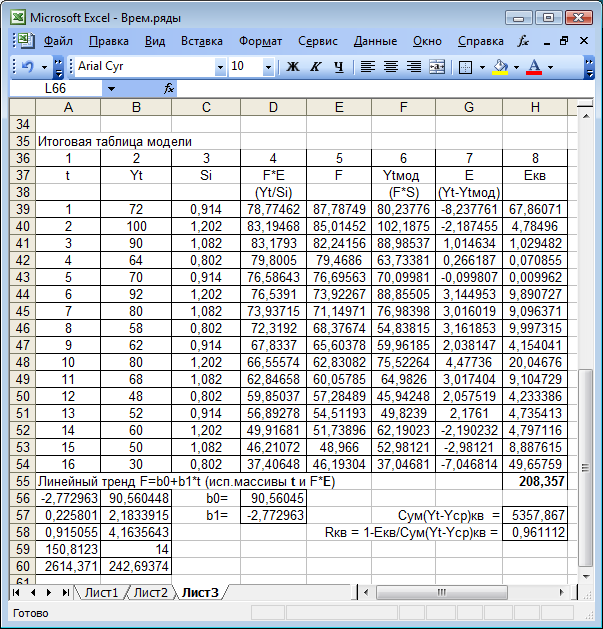
Рис. 5.19
Шаг 4. Определим компоненту F. Для этого по значениям 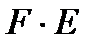 рассчитаем линейный тренд с использованием функции ЛИНЕЙН:
рассчитаем линейный тренд с использованием функции ЛИНЕЙН: 
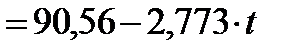 . Подставляя в это уравнение t = 1, 2, … получим 5 столбец.
. Подставляя в это уравнение t = 1, 2, … получим 5 столбец.
Шаг 5. Найдем значения уровней ряда, полученных по мультипликативной модели. Для этого прибавим к уровням F их сезонные составляющие Yt мод =  (6 столбец).
(6 столбец).
Из рис. 5.20 видно, что совпадение модельных и экспериментальных данных достаточно высокое.
Рис. 5.20
Свидетельством высокого качества модели также является близкое к единице значение коэффициента детерминации R2 = 0,96.
5.3. Контрольные задания
Задача 1. Экспорт, импорт, внешнеторговый оборот Австралии и Бельгии за 1961 – 1995 гг. характеризуются данными, представленными в табл. 5.6.
Таблица 5.6
| Год | Австралия, млн шиллингов | Бельгия, млн франков | |||||
| Экспорт | Импорт | Внешнеторговый оборот | Экспорт | Импорт | Внешнеторговый оборот | ||
Задание
1. Постройте график временного ряда.
2. Проверьте на аномальность уровней ряда и при их наличии произвести корректировку.
3. Проверьте наличие тренда.
4. Постройте коррелограмму. Охарактеризуйте структуру этого ряда.
5. Осуществите механическое сглаживание ряда с помощью скользящей средней.
6. Проведите расчет параметров трендов разной формы.
7. Оцените статистическую значимость трендов через F – критерий, значимость параметров трендов – через t – критерий.
8. Выберите лучшую форму тренда и выполните по ней интервальный прогноз для t = tпрогн.
Вариант 1.1
yt – экспорт Австралии; tпрогн – 1996 год; уровень значимости 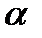 = 0,01.
= 0,01.
Вариант 1.2
yt – импорт Австралии; tпрогн – 1997 год; уровень значимости 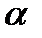 = 0,03.
= 0,03.
Вариант 1.3
yt – внешнеторговый оборот Австралии; tпрогн – 1998 год; уровень значимости 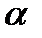 = 0,05.
= 0,05.
Вариант 1.4
yt – экспорт Бельгии; tпрогн – 1996 год; уровень значимости 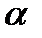 = 0,01.
= 0,01.
Вариант 1.5
yt – импорт Бельгии; tпрогн – 1997 год; уровень значимости 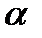 = 0,03.
= 0,03.
Вариант 1.6
yt – внешнеторговый оборот Бельгии; tпрогн – 1998 год; уровень значимости 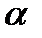 = 0,05.
= 0,05.
Задача 2. Реальный объем произведенного в России ВВП по кварталам в среднегодовых ценах 1995 года (трлн.рублей) представлен в табл. 5.7 (данные Федеральной службы государственной статистики: www.gks.ru).
Таблица 5.7
| 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | |
| Валовой внутренний продукт в рыночных ценах | 330,1 | 341,6 | 395,7 | 361,1 | 322,8 | 330,1 | 374,0 | 350,1 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 304,6 | 318,0 | 371,0 | 341,5 | 300,9 | 309,6 | 353,7 | 333,9 |
| в том числе: | ||||||||
| Производство товаров | 126,0 | 136,0 | 187,3 | 147,6 | 121,8 | 127,7 | 170,2 | 141,7 |
| из них: | ||||||||
| Пpомышленность | 93,3 | 90,3 | 93,2 | 95,3 | 92,7 | 88,3 | 87,4 | 94,0 |
| Сельское хозяйство | 5,5 | 11,7 | 57,5 | 20,9 | 5,2 | 11,0 | 53,5 | 20,9 |
| Стpоительство | 25,4 | 32,0 | 34,5 | 29,4 | 22,2 | 26,5 | 27,4 | 24,8 |
| Производство услуг | 178,6 | 182,0 | 183,7 | 193,9 | 179,1 | 181,9 | 183,5 | 192,2 |
| в том числе: | ||||||||
| Рыночные услуги | 142,4 | 145,5 | 146,9 | 156,8 | 141,6 | 144,3 | 145,8 | 154,6 |
| из них: | ||||||||
| Транспорт и связь | 40,6 | 41,2 | 41,4 | 39,7 | 39,1 | 39,2 | 39,2 | 38,1 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 64,7 | 67,3 | 71,0 | 79,4 | 66,1 | 69,3 | 72,8 | 79,4 |
| Нерыночные услуги | 36,2 | 36,5 | 36,8 | 37,1 | 37,5 | 37,6 | 37,7 | 37,6 |
| 1 квар-тал | 2 квар-ал | 3 квар-тал | 4 квар-тал | 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | |
| Валовой внутренний продукт в рыночных ценах | 321,4 | 327,3 | 384,7 | 362,6 | 316,7 | 324,2 | 350,8 | 329,7 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 301,2 | 307,0 | 362,9 | 345,3 | 297,5 | 305,0 | 331,8 | 314,9 |
| в том числе: | ||||||||
| Производство товаров | 118,4 | 124,0 | 176,7 | 146,4 | 119,2 | 122,2 | 152,1 | 130,4 |
| из них: | ||||||||
| Пpомышленность | 92,0 | 88,0 | 91,0 | 99,7 | 94,3 | 86,5 | 81,3 | 90,9 |
| Сельское хозяйство | 4,8 | 10,4 | 57,1 | 20,6 | 4,6 | 10,5 | 43,5 | 16,8 |
| Стpоительство | 20,0 | 23,9 | 26,9 | 24,6 | 18,9 | 23,7 | 25,6 | 21,2 |
| Производство услуг | 182,8 | 183,0 | 186,2 | 198,9 | 178,3 | 182,8 | 179,7 | 184,5 |
| в том числе: | ||||||||
| Рыночные услуги | 145,9 | 146,2 | 149,3 | 161,9 | 140,5 | 145,3 | 141,7 | 148,3 |
| из них: | ||||||||
| Транспорт и связь | 38,5 | 38,0 | 38,3 | 37,9 | 37,4 | 36,5 | 37,3 | 36,3 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 70,1 | 71,8 | 75,8 | 84,9 | 69,1 | 70,7 | 69,2 | 73,4 |
| Нерыночные услуги | 36,9 | 36,8 | 36,9 | 37,0 | 37,8 | 37,5 | 38,0 | 36,2 |
| 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | |
| Валовой внутренний продукт в рыночных ценах | 310,8 | 334,2 | 390,9 | 369,4 | 346,3 | 368,4 | 432,0 | 399,8 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 291,5 | 313,4 | 366,4 | 348,7 | 322,6 | 343,0 | 402,9 | 374,4 |
| в том числе: | ||||||||
| Производство товаров | 116,7 | 130,0 | 179,0 | 152,6 | 131,9 | 146,2 | 202,8 | 169,3 |
| из них: | ||||||||
| Пpомышленность | 91,7 | 92,4 | 101,0 | 104,0 | 103,4 | 102,7 | 112,7 | 113,6 |
| Сельское хозяйство | 5,4 | 12,7 | 48,8 | 21,4 | 6,0 | 13,7 | 55,9 | 23,9 |
| Стpоительство | 18,2 | 23,2 | 27,6 | 25,7 | 20,9 | 27,9 | 32,4 | 30,0 |
| Производство услуг | 174,8 | 183,4 | 187,4 | 196,1 | 190,7 | 196,8 | 200,1 | 205,1 |
| в том числе: | ||||||||
| Рыночные услуги | 136,5 | 145,2 | 148,9 | 158,7 | 151,7 | 157,9 | 161,0 | 167,6 |
| из них: | ||||||||
| Транспорт и связь | 39,4 | 39,8 | 42,0 | 40,5 | 42,4 | 41,6 | 44,5 | 43,1 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 62,8 | 65,6 | 70,0 | 78,4 | 74,3 | 74,7 | 78,0 | 83,3 |
| Нерыночные услуги | 38,3 | 38,2 | 38,5 | 37,4 | 39,0 | 38,9 | 39,1 | 37,5 |
Задание
1. Постройте график временного ряда.
2. Визуально из графика и с помощью коррелограммы охарактеризуйте структуру этого ряда.
3. Рассчитайте значения сезонной компоненты методом скользящей средней.
4. Выделите трендовую составляющую.
5. Выберите лучшую форму тренда и оцените ее параметры.
6. Постройте аддитивную модель этого ряда.
7. Постройте аддитивную модель с использованием фиктивных переменных.
8. Сделайте сравнительный анализ этих моделей.
9. Выполните точечный прогноз для t = tпрогн.
Вариант 2.1
yt - валовой внутренний продукт в рыночных ценах; tпрогн – I квартал 2001 года; уровень значимости 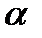 = 0,01.
= 0,01.
Вариант 2.2
yt - валовой внутренний продукт в основных ценах; tпрогн – II квартал 2001 года; уровень значимости 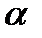 = 0,02.
= 0,02.
Вариант 2.3
yt - производство товаров; tпрогн – III квартал 2001 года; уровень значимости 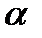 = 0,03.
= 0,03.
Вариант 2.4
yt - производство промышленных товаров; tпрогн – 4 квартал 2001 года; уровень значимости 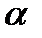 = 0,04.
= 0,04.
Вариант 2.5
yt - производство с/х товаров; tпрогн – 1и 2 кварталы 2001 года; уровень значимости 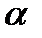 = 0,05.
= 0,05.
Задача 3. Реальный объем произведенного в России ВВП по кварталам в среднегодовых ценах 2000 года (млрд.рублей) представлен в табл. 5.8 (данные Федеральной службы государственной статистики: www.gks.ru).
Таблица 5.8
| 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | |
| Валовой внутренний продукт в рыночных ценах | 1651,2 | 1732,3 | 2020,2 | 1901,9 | 1728,3 | 1819,6 | 2141,7 | 1988,0 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 1468,4 | 1542,5 | 1810,1 | 1709,4 | 1534,5 | 1617,2 | 1916,6 | 1782,6 |
| в том числе: | ||||||||
| Производство товаров | 629,9 | 668,9 | 903,6 | 737,2 | 665,0 | 708,9 | 975,1 | 782,0 |
| из них: | ||||||||
| Пpомышленность | 492,4 | 489,0 | 528,6 | 539,2 | 519,2 | 516,3 | 552,9 | 561,3 |
| Сельское хозяйство | 48,9 | 62,3 | 238,5 | 70,5 | 51,6 | 67,4 | 272,3 | 76,8 |
| Стpоительство | 78,9 | 107,2 | 126,1 | 116,6 | 84,4 | 114,7 | 139,4 | 132,8 |
| 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | 1 квар-тал | 2 квар-тал | 3 квар-тал | 4 квар-тал | |
| Производство услуг | 838,5 | 873,6 | 906,5 | 972,2 | 869,5 | 908,3 | 941,5 | 1000,6 |
| в том числе: | ||||||||
| Рыночные услуги | 702,0 | 736,5 | 768,8 | 834,0 | 735,0 | 773,4 | 801,4 | 863,8 |
| из них: | ||||||||
| Транспорт и связь | 140,5 | 144,1 | 150,3 | 151,5 | 144,8 | 154,0 | 159,2 | 161,8 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 361,7 | 372,6 | 423,2 | 377,6 | 386,6 | 401,0 | 440,9 | |
| Нерыночные услуги | 136,5 | 137,1 | 137,7 | 138,2 | 134,5 | 134,9 | 140,1 | 136,8 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт в рыночных ценах | 1794,1 | 1899,9 | 2237,0 | 2110,8 | 1930,6 | 2051,7 | 2376,2 | 2274,2 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 1589,1 | 1686,4 | 2000,7 | 1895,3 | 1715,2 | 1818,7 | 2131,1 | 2045,6 |
| в том числе: | ||||||||
| Производство товаров | 685,3 | 736,1 | 1002,3 | 820,1 | 736,4 | 799,4 | 1077,9 | 896,8 |
| из них: | ||||||||
| Пpомышленность | 533,9 | 536,7 | 584,3 | 580,2 | 570,2 | 579,6 | 625,9 | 626,1 |
| Сельское хозяйство | 56,6 | 72,2 | 263,1 | 89,8 | 59,0 | 74,6 | 275,3 | 100,2 |
| Стpоительство | 85,0 | 116,6 | 144,3 | 138,6 | 96,5 | 133,7 | 165,2 | 158,4 |
| Производство услуг | 903,8 | 950,3 | 998,4 | 1075,2 | 978,8 | 1019,3 | 1053,2 | 1148,8 |
| в том числе: | ||||||||
| Рыночные услуги | 767,4 | 812,7 | 855,0 | 934,2 | 836,3 | 875,9 | 904,5 | 1002,6 |
| из них: | ||||||||
| Транспорт и связь | 151,4 | 162,5 | 170,4 | 171,6 | 161,6 | 175,3 | 184,6 | 191,3 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 400,5 | 412,7 | 433,6 | 490,3 | 457,9 | 463,4 | 470,3 | 534,8 |
| Нерыночные услуги | 136,4 | 137,6 | 143,4 | 141,0 | 142,5 | 143,4 | 148,7 | 146,2 |
| 1 квар- тал | 1 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт в рыночных ценах | 2071,6 | 2205,7 | 2545,1 | 2427,0 |
| в основных ценах (без снятия косвенно-измеряемых услуг финансового посредничества) | 1837,3 | 1960,7 | 2277,0 | 2186,4 |
| в том числе: | ||||
| Производство товаров | 792,2 | 861,6 | 1135,5 | 942,1 |
| из них: | ||||
| Пpомышленность | 612,2 | 621,5 | 658,3 | 656,3 |
| Сельское хозяйство | 58,6 | 74,6 | 288,7 | 102,0 |
| Стpоительство | 109,9 | 153,3 | 176,3 | 170,6 |
| Производство услуг | 1045,1 | 1099,1 | 1141,5 | 1244,3 |
| в том числе: | ||||
| Рыночные услуги | 899,6 | 952,3 | 989,1 | 1094,7 |
| из них: | ||||
| Транспорт и связь | 175,3 | 194,3 | 203,3 | 207,8 |
| Торговля (оптовая, розничная), общественное питание и заготовки | 499,0 | 511,1 | 519,3 | 591,3 |
| Нерыночные услуги | 145,5 | 146,8 | 152,4 | 149,6 |
Задание.
1. Постройте график временного ряда.
2. Визуально из графика и с помощью коррелограммы охарактеризуйте структуру этого ряда.
3. Рассчитайте значения сезонной компоненты методом скользящей средней.
4. Выделите трендовую составляющую.
5. Выберите лучшую форму тренда и оцените ее параметры.
6. Постройте аддитивную модель этого ряда.
7. Постройте аддитивную модель с использованием фиктивных переменных.
8. Сделайте сравнительный анализ этих моделей.
9. Выполните точечный прогноз для t = tпрогн.
Вариант 3.1
yt - валовой внутренний продукт в рыночных ценах; tпрогн – 1 квартал 2005 года; уровень значимости 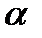 = 0,01.
= 0,01.
Вариант 3.2
yt - валовой внутренний продукт в основных ценах; tпрогн – 2 квартал 2005 года; уровень значимости 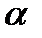 = 0,02.
= 0,02.
Вариант 3.3
yt - производство товаров; tпрогн – 3 квартал 2005 года; уровень значимости 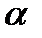 = 0,03.
= 0,03.
Вариант 3.4
yt - производство промышленных товаров; tпрогн – 4 квартал 2005 года; уровень значимости 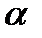 = 0,04.
= 0,04.
Вариант 3.5
yt - производство с/х товаров; tпрогн – 1и 2 кварталы 2005 года; уровень значимости 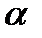 = 0,05.
= 0,05.
Задача 4. Номинальный объем использованного в России ВВП по кварталам (в текущих ценах, млрд.руб., до 1998г. – трлн.руб.) представлен в табл. 5.9 (данные Федеральной службы государственной статистики: www.gks.ru).
Таблица 5.9
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт | 235,0 | 324,3 | 421,1 | 448,1 | 425,3 | 468,4 | 548,9 | 565,2 |
| в том числе: | ||||||||
| Расходы на конечное потребление | 181,2 | 233,0 | 281,7 | 320,7 | 330,4 | 349,6 | 364,9 | 391,0 |
| домашних хозяйств | 126,0 | 163,7 | 200,9 | 229,2 | 230,0 | 242,9 | 256,1 | 278,8 |
| государственного управления | 50,7 | 63,6 | 74,2 | 84,0 | 91,8 | 97,5 | 99,5 | 102,6 |
| некоммерческих организаций, обслуживающих домашние хозяйства | 4,5 | 5,7 | 6,6 | 7,5 | 8,6 | 9,2 | 9,3 | 9,6 |
| Валовое накопление | 30,9 | 69,4 | 132,2 | 130,9 | 73,4 | 91,3 | 170,6 | 139,9 |
| валовое накопление основного капитала1) | 30,0 | 61,7 | 75,8 | 133,6 | 63,4 | 78,9 | 97,6 | 161,7 |
| изменение запасов материальных оборотных средств | 0,9 | 7,7 | 56,4 | -2,7 | 10,0 | 12,4 | 73,0 | -21,8 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Чистый экспорт | 18,9 | 19,2 | 5,2 | 5,2 | 13,0 | 16,0 | 19,4 | 36,4 |
| Экспорт | 88,5 | 113,9 | 101,9 | 114,1 | 110,2 | 123,5 | 134,7 | 155,1 |
| Импорт | 69,6 | 94,7 | 96,7 | 108,9 | 97,2 | 107,5 | 115,3 | 118,7 |
| Статистическое расхождение | 4,0 | 2,7 | 2,0 | -8,7 | 8,5 | 11,5 | -6,0 | -2,1 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт | 512,4 | 555,1 | 634,2 | 640,8 | 550,9 | 602,5 | 675,5 | 800,7 |
| в том числе: | ||||||||
| Расходы на конечное потребление | 413,3 | 426,9 | 452,3 | 483,6 | 420,1 | 427,0 | 503,6 | 653,1 |
| домашних хозяйств | 282,8 | 292,0 | 315,0 | 345,4 | 307,2 | 312,4 | 371,6 | 471,1 |
| государственного управления | 119,0 | 123,1 | 125,3 | 126,1 | 102,7 | 104,1 | 120,1 | 165,7 |
| некоммерческих организаций, обслуживающих домашние хозяйства | 11,5 | 11,8 | 12,0 | 12,1 | 10,2 | 10,5 | 11,9 | 16,3 |
| Валовое накопление | 83,4 | 107,8 | 186,0 | 137,6 | 127,2 | 162,8 | 119,7 | -16,2 |
| валовое накопление основного капитала1) | 77,1 | 90,1 | 116,0 | 145,3 | 73,6 | 90,0 | 115,2 | 145,9 |
| изменение запасов материальных оборотных средств | 6,3 | 17,7 | 70,0 | -7,7 | 53,6 | 72,8 | 4,5 | -162,1 |
| Чистый экспорт | 21,6 | 10,2 | 8,5 | 11,3 | -6,6 | -1,3 | 35,6 | 147,7 |
| Экспорт | 130,3 | 135,2 | 148,4 | 165,4 | 124,8 | 133,0 | 197,3 | 365,9 |
| Импорт | 108,7 | 125,0 | 139,9 | 154,1 | 131,4 | 134,3 | 161,7 | 218,2 |
| Статистическое расхождение | -5,9 | 10,2 | -12,6 | 8,3 | 10,2 | 14,0 | 16,6 | 16,1 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт | 901,3 | 1101,5 | 1373,1 | 1447,3 | 1527,4 | 1696,6 | 2037,8 | 2043,8 |
| в том числе: | ||||||||
| Расходы на конечное потребление | 708,0 | 766,3 | 852,5 | 958,9 | 997,7 | 1045,1 | 1167,3 | 1266,7 |
| домашних хозяйств | 536,7 | 580,5 | 655,3 | 753,7 | 724,0 | 760,9 | 857,6 | 952,7 |
| государственного управления | 158,6 | 172,0 | 182,6 | 190,0 | 255,2 | 265,0 | 289,5 | 292,8 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| некоммерческих организаций, обслуживающих домашние хозяйства | 12,7 | 13,8 | 14,6 | 15,2 | 18,5 | 19,2 | 20,2 | 21,2 |
| Валовое накопление | 69,4 | 170,1 | 313,8 | 162,0 | 177,0 | 283,2 | 470,1 | 435,4 |
| валовое накопление основного капитала1) | 101,9 | 139,1 | 194,0 | 258,9 | 179,7 | 252,5 | 346,3 | 453,5 |
| изменение запасов материальных оборотных средств | -32,5 | 31,0 | 119,8 | -96,9 | -2,7 | 30,7 | 123,8 | -18,1 |
| Чистый экспорт | 123,9 | 165,1 | 206,8 | 326,4 | 372,3 | 388,6 | 372,2 | 330,0 |
| Экспорт | 388,3 | 470,9 | 529,0 | 696,4 | 755,2 | 803,0 | 834,1 | 826,6 |
| Импорт | 264,4 | 305,8 | 322,2 | 370,0 | 382,9 | 414,4 | 461,9 | 496,6 |
| Статистическое расхождение | 0,0 | 0,0 | 0,0 | 0,0 | -19,6 | -20,3 | 28,2 | 11,7 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | ||
| Валовой внутренний продукт | 1900,9 | 2105,0 | 2487,9 | 2449,8 | 2259,5 | 2525,7 | 3009,2 | 3023,1 | |
| в том числе: | |||||||||
| Расходы на конечное потребление | 1306,3 | 1412,7 | 1523,9 | 1643,9 | 1691,0 | 1779,9 | 1907,0 | 2070,9 | |
| домашних хозяйств | 937,1 | 1023,2 | 1125,0 | 1233,0 | 1203,2 | 1273,8 | 1391,5 | 1539,9 | |
| государственного управления | 345,9 | 365,2 | 373,8 | 385,0 | 457,4 | 474,6 | 483,4 | 497,9 | |
| некоммерческих организаций, обслуживающих домашние хозяйства | 23,3 | 24,5 | 25,1 | 25,9 | 30,4 | 31,5 | 32,1 | 33,1 | |
| Валовое накопление | 253,7 | 409,6 | 682,7 | 617,1 | 333,5 | 456,4 | 745,5 | 635,1 | |
| валовое накопление основного капитала1) | 264,4 | 367,5 | 470,3 | 587,1 | 305,5 | 418,2 | 542,6 | 672,5 | |
| изменение запасов материальных оборотных средств | -10,7 | 42,1 | 212,4 | 30,0 | 28,0 | 38,2 | 202,9 | -37,4 | |
| Чистый экспорт | 357,1 | 294,7 | 274,5 | 207,4 | 235,7 | 290,7 | 329,7 | 311,4 | |
| Экспорт | 792,7 | 838,8 | 848,7 | 819,4 | 759,5 | 929,5 | 1043,2 | 1081,5 | |
| Импорт | 435,6 | 544,1 | 574,2 | 612,0 | 523,8 | 638,8 | 713,5 | 770,1 | |
| Статистическое расхождение | -16,2 | -12,0 | 6,8 | -18,6 | -0,7 | -1,3 | 27,0 | 5,7 | |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт | 2850,7 | 3107,8 | 3629,8 | 3655,0 | 3516.8 | 3969.8 | 4615.2 | 4946.4 |
| в том числе: | ||||||||
| Расходы на конечное потребление | 2071,1 | 2165,8 | 2289,9 | 2497,9 | 2584.7 | 2714.9 | 2919.6 | 3182.3 |
| домашних хозяйств | 1476,6 | 1547,8 | 1663,3 | 1852,4 | 1864.8 | 1975.4 | 2165.6 | 2399.8 |
| государственного управления | 557,4 | 579,7 | 587,7 | 605,8 | 684.1 | 702.8 | 716.6 | 744.0 |
| некоммерческих организаций, обслуживающих домашние хозяйства | 37,1 | 38,3 | 38,9 | 39,7 | 35.8 | 36.7 | 37.4 | 38.5 |
| Валовое накопление | 382,5 | 580,3 | 985,2 | 807,1 | 493.0 | 760.3 | 1206.5 | 1099.1 |
| валовое накопление основного капитала1) | 376,2 | 530,9 | 672,1 | 853,1 | 496.3 | 690.5 | 850.3 | 1093.4 |
| изменение запасов материальных оборотных средств | 6,3 | 49,4 | 313,1 | -46,0 | -3.3 | 69.8 | 356.2 | 5.7 |
| Чистый экспорт | 414,0 | 351,5 | 360,2 | 376,3 | 425.5 | 495.0 | 557.5 | 608.5 |
| Экспорт | 1081,0 | 1103,1 | 1206,6 | 1265,2 | 1180.0 | 1391.3 | 1585.6 | 1703.5 |
| Импорт | 667,0 | 751,6 | 846,4 | 888,9 | 754.5 | 896.3 | 1028.1 | 1095.0 |
| Статистическое расхождение | -16,9 | 10,2 | -5,5 | -26,3 | 13.6 | -0.4 | -68.4 | 56.5 |
| 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | 1 квар- тал | 2 квар- тал | 3 квар- тал | 4 квар- тал | |
| Валовой внутренний продукт | 4459.7 | 5080.4 | 5873.0 | 6212.3 | 5811.9 | 6389.5 | 7299.2 | 7402.9 |
| в том числе: | ||||||||
| Расходы на конечное потребление | 3170.8 | 3460.5 | 3686.6 | 4001.0
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228270']=__lxGc__['s']['_228270']||{'b':{}})['b']['_698049']={'i':__lxGc__.b++};
|
Главная страница Случайная страница Контакты