
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткие теоретические сведения
Образцы изоляции (газовой, жидкой, твердой) и изоляционные конструкции подвергаются различного рода испытаниям. Например, электрическая прочность газовых промежутков и конструкций при постоянном или переменном напряжении определяется при непрерывном подъеме напряжения до пробоя. Скорость нарастания напряжения в этом случае, как правило, не лимитируется. При повторных испытаниях наблюдаемые значения пробивных напряжений будут неодинаковы. Разброс пробивных напряжений при такого вида испытаниях определяется многими причинами: неидентичностью промежутков от испытания к испытанию; нестабильной погрешностью измерительного прибора; субъективностью оператора; статистическими закономерностями, связанными с возникновением и развитием самого процесса разряда и т.п., - т.е. разброс зависит от многих случайных факторов.
Среднее значение пробивного напряжения
 ,
,
часто приводится как характеристики электрической прочности образца или изоляционной конструкции. Однако для многих практических случаев важно знать, помимо  , характеристики, связанные с разбросом пробивных напряжений; минимальное пробивное напряжение Up min; вероятность пробоя при подъеме напряжения до данной величины Ui-P(Up
, характеристики, связанные с разбросом пробивных напряжений; минимальное пробивное напряжение Up min; вероятность пробоя при подъеме напряжения до данной величины Ui-P(Up  Ui); среднеквадратичное отклонение
Ui); среднеквадратичное отклонение
 ,
,
которое является мерой крутизны зависимости P(Up  Ui).
Ui).
Зависимость вероятности пробоя от величины напряжения по экспериментальным данным строится следующим методом. Разделим диапазон полученных N значений пробивных напряжений на n равных элементарных диапазонов ΔU по соотношению
 .
.
Каждому из этих элементарных диапазонов пробивного напряжения будет соответствовать число пробоев Δn1; Δn2… Δnn и
 .
.
Величина  приблизительно равна вероятности того, что пробой произойдет в диапазоне значения напряжения от Uk до Uk+1 .
приблизительно равна вероятности того, что пробой произойдет в диапазоне значения напряжения от Uk до Uk+1 .
При условиях нормировки ΔU=1 и  получается экспериментальная гистограмма (рис.3.1) распределения плотности вероятности пробоев. Суммируя pk от p1 до pi получаем:
получается экспериментальная гистограмма (рис.3.1) распределения плотности вероятности пробоев. Суммируя pk от p1 до pi получаем:  - приближенную вероятность того, что пробой произойдет при Up. Ступенчатый график
- приближенную вероятность того, что пробой произойдет при Up. Ступенчатый график  дает экспериментальную зависимость Pi от напряжения. Из теории вероятности известно, что при
дает экспериментальную зависимость Pi от напряжения. Из теории вероятности известно, что при  функция Pk(U) представляет собой распределение плотности вероятности или дифференциальную кривую распределения вероятностей пробоя.
функция Pk(U) представляет собой распределение плотности вероятности или дифференциальную кривую распределения вероятностей пробоя.

Рис. 3.1. Построение экспериментальных гистограмм распределения вероятности пробоев и аппроксимирующих кривых дифференциального и интегрального распределений
При этом

интегральная кривая распределения вероятности пробоя. В общем случае эти кривые экспериментально получены быть не могут (  ). Однако, исходя из физических предпосылок, экспериментальные гистограммы для рk и
). Однако, исходя из физических предпосылок, экспериментальные гистограммы для рk и  могут быть аппроксимированы каким-либо математическим законом распределения вероятностей.
могут быть аппроксимированы каким-либо математическим законом распределения вероятностей.
Многочисленные исследования показали, что при многократных пробоях воздушных промежутков зависимость вероятности возникновения разряда от напряжения разряда в пределах  удовлетворительно описывается функцией нормального распределения Гаусса
удовлетворительно описывается функцией нормального распределения Гаусса
 ,
,
где  и σ - параметры распределения.
и σ - параметры распределения.
Точность определения найденных значений  и σ по сравнению с истинным зависит от N. Например, относительная погрешность определения σ и
и σ по сравнению с истинным зависит от N. Например, относительная погрешность определения σ и  с надежностью 0,95 находится по соотношениям
с надежностью 0,95 находится по соотношениям
 ;
;
 .
.
Соответствующие абсолютные погрешности
 ;
;  .
.
Построение кривых нормального распределения по известным параметрам σ и  производится с использованием соответствующих таблиц, приведенных в пособиях и справочниках по теории вероятности и математической статистике (некоторые табличные значения приведены в приложении к данной работе).
производится с использованием соответствующих таблиц, приведенных в пособиях и справочниках по теории вероятности и математической статистике (некоторые табличные значения приведены в приложении к данной работе).
При аналогичных испытаниях образцов жидкости (например, трансформаторного масла) разброс пробивных напряжений и  зависят не только от всех факторов, перечисленных для газообразных образцов, но и от времени воздействия (скорости подъема) напряжения.
зависят не только от всех факторов, перечисленных для газообразных образцов, но и от времени воздействия (скорости подъема) напряжения.
Формирование разряда в технически чистой жидкости при сравнительно длительном воздействии напряжения (секунды и более) связано с наличием и расположением в момент испытания в промежутке различного рода примесей, пузырьков, их накоплением, деформацией и т.д.
Поэтому разброс пробивных напряжений в жидкости будет больше, чем в газе, и, повторяем, будет сильно зависеть от скорости подъема напряжения. Следовательно, при испытаниях жидких образцов скорость нарастания напряжения должна быть строго лимитирована. Кривая  при испытаниях жидкой изоляции также удовлетворительно аппроксимируется усеченным (от -3s до +3s) интегральным распределением Гаусса, хотя отличие действительной кривой от нормального закона здесь может быть более заметно.
при испытаниях жидкой изоляции также удовлетворительно аппроксимируется усеченным (от -3s до +3s) интегральным распределением Гаусса, хотя отличие действительной кривой от нормального закона здесь может быть более заметно.
Для большинства практически важных случаев при известной (найденной) кривой распределения вероятностей пробоев по напряжениям за минимальное разрядное напряжение при идентичных условиях опыта принимается 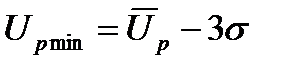 .
.
Содержание работы и порядок ее выполнения
1. Получить экспериментальные данные для определения статических характеристик пробоя при испытании воздушных и масляных промежутков при плавном подъеме напряжения промышленной частоты.
2. Построить по экспериментальным данным гистограммы для pk, рассчитать Pi(Up<Ui) и  и оценить точность их определения.
и оценить точность их определения.
3. По найденным  и σ , используя таблицы, построить график нормального распределения (интегральная кривая) и определить Umin.
и σ , используя таблицы, построить график нормального распределения (интегральная кривая) и определить Umin.
4. Для полученных опытных данных по программе ЭВМ (по отдельной инструкции) построить гистограммы плотности вероятности и вероятности пробоев для разных величин n. Рассчитать параметры  , σ,
, σ,  ,
,  и получить кривые дифференциального и интегрального распределения Гаусса.
и получить кривые дифференциального и интегрального распределения Гаусса.
Работа выполняется на высоковольтной испытательной установке, которая приведена на рис. 3.2.

Рис.3.2. Принципиальная схема испытательной установки
Включение обеспечивается с помощью рубильника QS1, кнопки SB1 (ВКЛ) и магнитного пускателя КМ. Отключение и защита – с помощью токового реле КА, автомата SF1 и кнопки SB2 (ОТКЛ).
При выполнении опытов использовать заданные преподавателем промежутки. Рекомендуется для получения приемлемых оценок выполнить N=50 опытов для каждого промежутка. Скорость подъема напряжения и условия проведения опытов выдержать, по возможности, постоянным. Для построения гистограммы по данным 50 опытов n принимается обычно в пределах 7-9. При работе с программой ЭВМ число диапазонов n можно менять.
Результаты измерений записать в табл.3.1, а расчеты – в табл. 3.2.
Таблица 3.1
| № п/п | U1, В | U2, кВ U2=kгрU1 | U2i, кВ | № п/п | U1, В | U2, кВ | U2i, кВ |

| 
| ||||||
| … | 
| … | 
|
Таблица 3.2
| № п/п | 
| 
| 
| 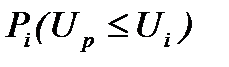
| 
| 
| 
| 
|
По полученным и рассчитанным данным построить гистограммы для pk(ΔUk) и Pi(Up  Ui), интегральную кривую нормального распределения Гаусса в пределах (
Ui), интегральную кривую нормального распределения Гаусса в пределах (  )…(
)…(  ).
).
Вероятность попадания нормально распределенной случайной величины U (в нашем случае - вероятность пробоя) в интервал (U1, U2) вычисляется по формуле
 ,
,
где  - функция Лапласа (интеграл вероятности), некоторые значения которой приведены в таблице.
- функция Лапласа (интеграл вероятности), некоторые значения которой приведены в таблице.
Таблица 3.3
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| 0,0797 | 0,1585 | 0,2358 | 0,3108 | 0,3829 | 0,4515 | 0,5161 | 0,5763 | 0,6319 | ||
| 0,6827 | 0,7287 | 0,7699 | 0,8064 | 0,8385 | 0,8664 | 0,8904 | 0,6109 | 0,9231 | 0,9426 | |
| 0,9545 | 0,9643 | 0,9786 | 0,9876 | 0,9836 | 0,9876 | 0,9907 | 0,9931 | 0,9949 | 0,9963 | |
| 0,9973 | 0,9981 | 0,9986 | 0,9990 | 0,9993 | 0,9995 | 0,9997 | 0,9998 | 0,9998 | 0,9999 |
Приведем расчет одной точки. Допустим, по экспериментальным данным s=5 кВ,  =30 кВ. Определим
=30 кВ. Определим  .
.

Интеграл вероятности является функцией нечетной и
 .
.
Аналогично рассчитываются все остальные точки в пределах от - 3σ – до +3σ.
Содержание отчета
1. Цель работы и методика ее проведения.
2. Схема испытательной установки и параметров основного оборудования
3. Результаты испытаний и расчетов в виде таблиц и графиков.
4. Расчетные формулы и примеры расчета основных величин (  , σ,
, σ,  ).
).
5. Основные результаты, полученные по программе ЭВМ.
6. Выводы по работе.
Контрольные вопросы
1. Чем определяется разброс пробивных напряжений образцов изоляции?
2. Почему разброс пробивных напряжений жидкой изоляции больше, чем воздушной?
3. Является ли исчерпывающей характеристикой изоляционных возможностей конструкции величина  ?
?
4. Поясните смысл основных параметров нормального распределения (σ,  ).
).
5. Почему нормальное распределение Гаусса удовлетворительно аппроксимирует экспериментальную кривую P (Up = Ui) в пределах  ?
?
6. Часто очень важной величиной для оценки изоляции является величина Up,min. Почему?
7. Определите необходимый объем испытаний для оценки  и σ при заданной величине погрешности.
и σ при заданной величине погрешности.
Литература: [1], с.41-43; [3], с.78-81;
[6], справочники и пособия по теории вероятности и математической статистике.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Тульский государственный университет»
Факультет систем автоматического управления
(ИВТС им. В.П. Грязева)
Кафедра «Электроэнергетика»
Дата добавления: 2014-12-23; просмотров: 395; Мы поможем в написании вашей работы!; Нарушение авторских прав |