Средние показатели

Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.

Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:

· средняя арифметическая,

· средняя гармоническая,

· средняя геометрическая,

· средняя хронологическая;

· средняя квадратическая, кубическая и т.д.

Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):

i=

где х _i - i-ый вариант осредняемого признака (i= )

f _i - вес i-го варианта.

Кроме степенных средних в экономической практике также используются средние структурные, среди которых наиболее распространены мода и медиана.

Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая простая используется в тех случаях, когда расчет осуществляется по несгруппированным данным, и имеет вид:

(3.1)

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться в совокупности несколько раз. В подобных случаях расчет средней производится по сгруппированным данным, то есть данным представленным в виде дискретных или интервальных вариационных рядов распределения.

Средняя арифметическая взвешенная определяется по формуле:

(3.2)

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы):

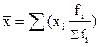. (3.3)

Таким образом, среднюю арифметическую невзвешенную можно использовать в том случае, когда точно установлено отсутствие весов или их равенство.

При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам путем определения средней арифметической простой между нижней и верхней границами каждого интервала.

Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства:

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

(3.4)

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

(3.5)

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С.

4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

(3.6)

5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

(3.7)

6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

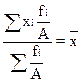(3.8)

Исходя из данного свойства, можно заключить, что если все веса равны между собой, то расчеты по средней арифметической взвешенной и средней арифметической невзвешенной приведут к одному и тому же результату.

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель, определяется по формуле:

, где w_i=x_if_i (3.9)

Данная формула используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов.

Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:

(3.10)

Средняя геометрическая:

- невзвешенная (3.11)

- взвешенная

Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе.

Средняя квадратическая:

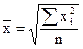- невзвешенная (3.12)

- взвешенная

Наиболее широко этот вид средней используется при расчете показателей вариации.