Показатели вариации в анализе взаимосвязей

Показатели вариации могут быть использованы не только в анализе колеблемости изучаемого признака, но и для оценки степени влияния одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.

При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками - факторным и результативным.

Для выявления взаимосвязи исходная совокупность делится на две или более группы по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

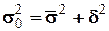(4.18)

где - общая дисперсия;

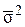- средняя из внутригрупповых дисперсий;

- межгрупповая дисперсия.

Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней:

(4.19)

где 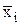- среднее значение результативного признака по i-ой группе;

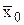- общая средняя по совокупности в целом;

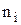- объем (численность) i-ой группы.

Если факторный признак, по которому производилась группировка, не оказывает никакого влияния не признак результативный, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равна нулю.

Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

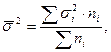(4.20)

где -дисперсия результативного признака в i-ой группе;

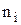-объем (численность) i-ой группы.

Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

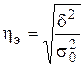(4.21)

Данный показатель может принимать значения от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.