Основные показатели вариации

Вариация значений признака представляет наибольший интерес при исследовании социально-экономических явлений и процессов.

Используемые в статистическом анализе показатели вариации можно разделить на три группы:

- показатели размаха;

- показатели, характеризующие отклонения от среднего уровня;

- относительные показатели вариации.

К показателям размаха относят:

- вариационный размах;

- децильный размах;

- квартильный размах.

К показателям, характеризующим отклонения от среднего уровня, относят:

- среднее линейное отклонение;

- среднее квадратическое отклонение;

- дисперсию.

К относительным показателям относят:

- относительный квартильный размах;

- линейный коэффициент вариации;

- коэффициент вариации.

Вариационный размах или размах вариации характеризует абсолютную разницу между максимальным и минимальным значениями признака в изучаемой совокупности:

(4.1)

Основным недостатком данного показателя является то обстоятельство, что максимальные и минимальные значения признака могут быть обусловлены случайными обстоятельствами и в этой связи могут искажать типичный для изучаемой совокупности размах вариации.

Децильный размах (D) характеризует абсолютную разницу между значениями девятой (верхней) и первой (нижней) децилями:

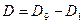(4.2)

Таким образом, децильный размах характеризует разброс 80% данных и, является более предпочтительным по сравнению с вариационным размахом, так как практически не зависит от экстремальных значений.

Квартильный размах или интерквартильный разбрас (interquartile rang - IQR) характеризует абсолютную разницу между третьим (верхним) и первым (нижним) квартилями:

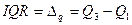(4.3)

Третья или верхняя квартиль (Q3) показывает значение признака больше которого расположено 25% значений. Таким образом квартильный размах характеризует разброс 50% центральных значений.

Среди показателей разброса наиболее часто в практическом анализе используют квартильный размах.

Показатели разброса графически можно представить в виде секционной диаграммы (boxplot). В секционной диаграмме пунктирная линия представляет медиану, прямоугольник характеризует квартильный разброс, а вертикальные линии, выходящие из прямоугольника (их часто называют «усами»), характеризуют границы разброса. Если в данных нет аномальных значений, то «усы» соответствуют минимальному и максимальному значениям признака. Обычно к аномальным значениям относят данные, отклонения которых от нижнего и верхнего квартиля больше чем в 1,5 раза превышают квартильный разброс. Если такие данные существуют, то они показываются в виде отдельных точек. В этом случае «усы» принимаются равными

нижний: (4.4)

верхний: (4.5)

Среднее линейное отклонение. Для абсолютной количественной оценки различий между всеми без исключения значениями признака в изучаемой совокупности используется оценка отклонений фактических значений от их среднего уровня. Чем больше различия между вариантами признака, тем больше и их отклонения от среднего уровня. Однако, как отмечалось в главе «Средние показатели», сумма отклонений фактических значений от средней всегда равна 0. Существует два основных подхода к усреднению отклонений фактических значений от средней. Первый состоит в том, что используют абсолютные значения отклонений и в результате получают показатель который называется среднее линейное отклонение. Второй состоит в том, что отклонения возводят в квадрат и в результате получают дисперсию и среднее квадратическое отклонение.

Среднее линейное или среднее абсолютное отклонение (mean absolute deviation – ) представляет собой среднее арифметическое из абсолютных значений отклонений фактических вариантов признака от среднего значения. В зависимости от характера исходных данных для расчета используют простую или взвешенную форму:

- простая форма; (4.6)

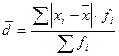- взвешенная форма, (4.7)

Если данные не сгруппированы, то используют простую формулу, если сгруппированы – то взвешенную.

Дисперсия (variance) представляет собой средний квадрат отклонений значений признака от средней величины.

В зависимости от характера исходных данных для расчета используют простую или взвешенную формулу:

- простая форма; (4.8)

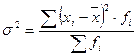- взвешенная форма, (4.9)

Для расчета дисперсии в отдельных случаях удобнее использовать формулу, которая представляет собой алгебраическое преобразование выражений (4.8) и (4.9):

, где (4.10)

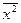- средняя квадратическая.

В зависимости от характера исходных данных для расчета средней квадратической используются простая или взвешенная формы:

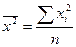- простая, (4.11)

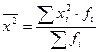- взвешенная. (4.12)

Если данные не сгруппированы, то используют простую форму, если сгруппированы – то взвешенную.

Возведение отклонений фактических значений от средней в квадрат приводит к тому, что дисперсия имеет тоже наименования, что и изучаемый признак, но возведенное в квадрат. Это затрудняет экономическую интерпретацию полученных результатов. Поэтому наиболее удобным и широко распространенным на практике показателем вариации является среднее квадратическое отклонение, которое определяется как квадратный корень из дисперсии и имеет ту же размеренность, что и изучаемый признак.

Среднее квадратическое отклонение характеризует среднее отклонение фактических значений признака в статистической совокупности от их среднего значения и рассчитывается на основе следующих формул:

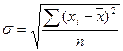- простая форма, (4.13)

- взвешенная форма (4.14)

(4.15)

Среднее квадратическое отклонение также называют стандартным отклонением (standard deviation).

Среднее квадратическое отклонение и среднее линейное отклонение близки друг другу по экономическому смыслу и между ними есть определенная связь. Для симметричных или умеренно ассиметричных распределений .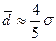

Среднее квадратическое отклонение более широко применяется в статистическом анализе по сравнению со средним линейным отклонением благодаря своим математических свойствам. Так среднее квадратическое отклонение является одним из параметров многих распределений и в первую очередь нормального распределения. В нормальном распределении примерно 2/3 всех значений отклоняются от среднего уровня не больше, чем на одну величину среднего квадратического отклонения. Приблизительно 95% всех значений отклоняются от среднего уровня не более чем на две величины среднего квадратического отклонения. И, наконец, около 99,7% всех значений лежат в пределах трех средних квадратических отклонений.

Коэффициенты вариации. Рассмотренные выше показатели позволяют получить абсолютное значение вариации, т.е. оценивают ее в единицах измерения исследуемого признака. Чтобы оценить масштабы вариации используют относительные показатели вариации, которые измеряют изменчивость значений признака в относительном выражении по сравнению со средним уровнем, что во многих случаях является более предпочтительным. Для оценки относительных размеров вариации используют линейный коэффициент вариации и квадратический коэффициент вариации. Последний показатель получил более широкое распространение, поэтому его обычно называют коэффициент вариации, опуская слово квадратический. Относительные показатели вариации, как правило, рассчитывают в процентах.

Линейный коэффициент вариации измеряют через соотношение среднего линейного отклонения и средней:

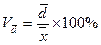(4.16)

Коэффициент вариации измеряют через соотношение среднего квадратического отклонения и средней:

(4.17)

Информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные по одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени. Например, исследуется динамика вариации курса доллара по годам или по месяцам или сравнивается вариация показателей компаний различных отраслей или регионов.