
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параметрические методы изучения связи
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков.
Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.
В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
 (5.4)
(5.4)
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
 (5.5)
(5.5)
Между линейным коэффициентом корреляции и коэффициентом регрессии существует определенная зависимость, выражаемая формулой:
 (5.6)
(5.6)
где  - коэффициент регрессии в уравнении связи;
- коэффициент регрессии в уравнении связи;
 - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака.
- среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака.
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: [  ]. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно осуществлять следующим образом (табл.5.2):
]. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений коэффициента корреляции можно осуществлять следующим образом (табл.5.2):
Таблица 5.2
Оценка линейного коэффициента корреляции
| Значение линейного коэффициента связи | Характеристика связи | Интерпретация связи |
| r = 0 | отсутствует | - |
| 0<r<1 | прямая | с увеличением x увеличивается y |
| -1<r<0 | обратная | с увеличением x уменьшается y и наоборот |
| r=1 | функциональная | каждому значению факторного признака строго соответствует одно значение результативного признака |
В случае наличия линейной и нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение.
Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда  характеризует отклонения групповых средних результативного показателя от общей средней:
характеризует отклонения групповых средних результативного показателя от общей средней:
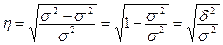 (5.7)
(5.7)
где  - корреляционное отношение;
- корреляционное отношение;
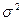 - общая дисперсия;
- общая дисперсия;
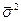 - средняя из частных (групповых) дисперсий;
- средняя из частных (групповых) дисперсий;
 - межгрупповая дисперсия (дисперсия групповых средних).
- межгрупповая дисперсия (дисперсия групповых средних).
Все эти дисперсии есть дисперсии результативного признака.
Теоретическое корреляционное отношение определяется по формуле:
 (5.8)
(5.8)
где  - дисперсия выровненных значений результативного признака, то есть рассчитанных по уравнению регрессии;
- дисперсия выровненных значений результативного признака, то есть рассчитанных по уравнению регрессии;
 - дисперсия эмпирических (фактических) значений результативного признака.
- дисперсия эмпирических (фактических) значений результативного признака.
Корреляционное отношение изменяется в пределах от 0 до 1  . Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.
. Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции.
Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков.
Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:
 (5.9)
(5.9)
где  - парные коэффициенты корреляции между признаками.
- парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен:  .
.
Приближение  к единице свидетельствует о сильной зависимости между признаками.
к единице свидетельствует о сильной зависимости между признаками.
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками  и
и  при фиксированном значении других
при фиксированном значении других  факторных признаков, то есть когда влияние
факторных признаков, то есть когда влияние  исключается, то есть оценивается связь между
исключается, то есть оценивается связь между  и
и  в «чистом виде».
в «чистом виде».
В случае зависимости  от двух факторных признаков
от двух факторных признаков  и
и  коэффициенты частной корреляции имеют вид:
коэффициенты частной корреляции имеют вид:

 (5.10)
(5.10)
где  - парные коэффициенты корреляции между указанными в индексе переменными.
- парные коэффициенты корреляции между указанными в индексе переменными.
В первом случае исключено влияние факторного признака  , во втором -
, во втором -  .
.
Дата добавления: 2014-12-23; просмотров: 381; Мы поможем в написании вашей работы!; Нарушение авторских прав |