
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы изучения связи качественных признаков
При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.
Коэффициент ассоциации и контингенции. Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяются коэффициенты ассоциации и контингенции.
Для их вычисления строится таблица, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, то есть состоящим из двух качественно отличных друг от друга значений признака.
Таблица 5.3
Таблица для вычисления коэффициентов ассоциации и контингенции
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Коэффициенты вычисляются по формулам:
ассоциации: 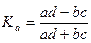 (5.14)
(5.14)
контингенции: 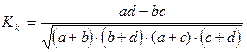 (5.15)
(5.15)
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если 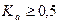 или
или 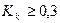 .
.
Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициента взаимной сопряженности Пирсона-Чупрова. Этот коэффициент вычисляется по следующей формуле:
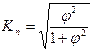 ;
; 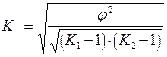 (5.16)
(5.16)
где 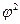 - показатель взаимной сопряженности;
- показатель взаимной сопряженности;
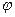 - определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину
- определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот, соответствующего столбца и строки. Вычитая из этой суммы «1», получим величину 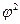 :
:
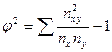 ;
;
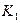 - число значений (групп) первого признака;
- число значений (групп) первого признака;
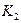 - число значений (групп) второго признака.
- число значений (групп) второго признака.
Чем ближе величина 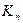 и Kч к 1, тем теснее связь.
и Kч к 1, тем теснее связь.
Таблица 5.4
Вспомогательная таблица для расчета коэффициента
взаимной сопряженности
| у х | I | II | III | Всего |
| I | 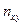
| 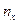
| ||
| II | 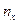
| |||
| III | 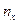
| |||
| Итого | 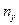
| 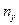
| 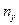
| 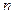
|
Особое значение для оценки связи имеет биссериальный коэффициент корреляции, который дает возможность оценить связь между качественным альтернативным и количественным варьирующим признаками. Данный коэффициент вычисляется по формуле:
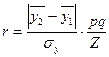 (5.17)
(5.17)
где 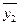 и
и 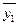 - средние в группах;
- средние в группах;
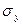 - среднее квадратическое отклонение фактических значений признака от среднего уровня;
- среднее квадратическое отклонение фактических значений признака от среднего уровня;
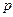 - доля первой группы;
- доля первой группы;
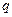 - доля второй группы;
- доля второй группы;
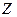 - табулированные (табличные) значения
- табулированные (табличные) значения 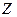 -распределения в зависимости от
-распределения в зависимости от 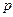 .
.
Величина биссериального коэффициента корреляции также подтверждает умеренную тесноту связи между изучаемыми признаками.
Дата добавления: 2014-12-23; просмотров: 383; Мы поможем в написании вашей работы!; Нарушение авторских прав |