Средние показатели рядов динамики

Каждый ряд динамики можно рассматривать как некую совокупность m меняющихся во времени показателей, которые можно обобщать в виде средних величин. Для обобщения данных по рядам динамики рассчитываются: средний уровень ряда; средний абсолютный прирост; средний темп роста и прироста.

Средний уровень ряда динамики ( 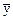) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени.

Для разных видов рядов динамики средний уровень рассчитывается неодинаково.

· Для интервальных равноотстоящих рядов средний уровень находится по формуле простой средней арифметической.

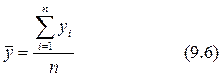
· Для интервальных неравноотстоящих рядов средний уровень находится по формуле взвешенной средней арифметической.

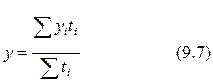
где у_i - уровень ряда динамики;

n - число уровней;

t_i - длительность интервала времени между уровнями.

Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической простой:

(9.8)

· Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяются по формуле средней хронологической взвешенной:

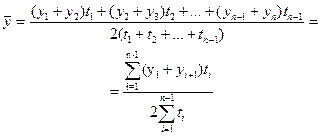(9.9)

где y_i, y_n - уровни рядов динамики;

t_i - длительность интервала времени между уровнями.

Обобщающим показателем скорости изменения явления во времени является средний абсолютный прирост за весь период, ограничивающий ряд динамики. Для его определения можно воспользоваться формулой средней арифметической простой:

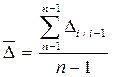(9.10.)

или

(9.11)

Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень динамического ряда.

Необходимость исчисления среднего темпа роста возникает вследствие того, что темпы роста из года в год колеблются. Кроме того, средний темп роста часто нужно определять в тех случаях, когда имеются данные об уровне в начале какого-либо периода и в конце его, а промежуточные данные отсутствуют.

Средний темп (коэффициент) роста рассчитывается по формуле средней геометрической из цепных коэффициентов роста:

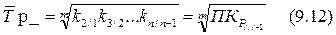
Поскольку всякий темп роста является отношением уровней ряда динамики, так, что 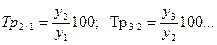в формуле средней геометрической темпы роста заменяются соответствующим отношением уровней. Заменив темпы роста выражающими их отношениями и учитывая, что эти величины перемножаются, найдем подкоренное выражение как:

Следовательно, средний темп роста может быть выражен формулой:

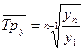(9.13)

Когда приходится вести расчет средних темпов роста по периодам различной продолжительности (разноотстоящие ряды динамики), то пользуются средними геометрическими, взвешенными по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:

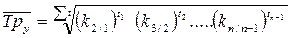(9.14)

где t - интервал времени, в течении которого сохраняется данный темп роста;

S - сумма отрезков времени периода.

Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо вначале найти средний темп роста, а затем уменьшить его на единицу или 100%:

(9.15)