Глава 16. Оценка точности и надежности прогнозов

Важным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов.

Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными ( ) и фактическими (у_t) значениями исследуемого показателя. Данный подход возможен только в двух случаях:

а) период упреждения известен, уже закончился и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя;

б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования.

В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза.

Полученные, таким образом, ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду.

В случае если, ретроспективное прогнозирование осуществлять по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков.

Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:

- аналитические;

- сравнительные;

- качественные.

Аналитические показатели точности прогноза позволяют количественно определить величину ошибки прогноза. К ним относятся следующие показатели точности прогноза:

Абсолютная ошибка прогноза (D^*) определяется как разность между эмпирическим и прогнозным значениями признака и вычисляется по формуле:

, (16.1)

где у_t – фактическое значение признака;

- прогнозное значение признака.

Относительная ошибка прогноза (d^*_отн) может быть определена как отношение абсолютной ошибки прогноза (D^*):

_- к фактическому значению признака (у_t):

(16.2)

- к прогнозному значению признака ( )

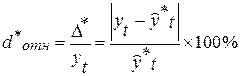(16.3)

Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как на изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели.

Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (К_к), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле:

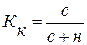(16.4)

Значение К_к = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяющегося в пределах от 0 до 1.

Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков.

Средним показателем точности прогноза является средняя абсолютная ошибка прогноза ( ), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:

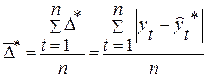, (16.5)

де n – длина временного ряда.

Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.

Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле:

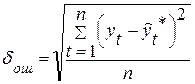(16.6)

Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение:

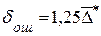(16.7)

Недостатками средней абсолютной и средней квадратической ошибками прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений.

Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида:

(16.8)

Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам. Интерпретация оценки точности прогноза на основе данного показателя представлена в следующей таблице:

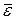,%	Интерпретация точности
< 10 10 – 20 20 – 50 > 50	Высокая Хорошая Удовлетворительная Не удовлетворительная

В качестве сравнительного показателя точности прогноза используется коэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:

, (16.9)

где - средний уровень ряда динамики прогнозных оценок.

Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.

Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях:

1. Коэффициент несоответствия (КН₁), определяемый как отношение средней квадратической ошибки к квадрату фактических значений признака:

(16.10)

КН = о, если , то есть полное совпадение фактических и прогнозных значений признака.

КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов.

КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет.

2.Коэффициент несоответствия КН₂ определяется как отношение средней квадратической ошибки прогноза к сумме квадратов

отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период:

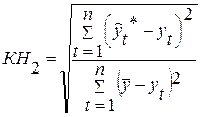, (16.11)

где - средний уровень исходного ряда динамики.

Если КН > 1, то прогноз на уровне среднего значения признака дал бы лучший результат, чем имеющийся прогноз.

3.Коэффициент несоответствия (КН₃), определяемый как отношение средней квадратической ошибке прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда:

, (16.12)

где 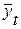- теоретические уровни временного ряда, полученные по

модели тренда.

Если КН > 1, то прогноз методом экстраполяции тренда дает хороший результат.