
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды степенных средних. Важным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов.
Важным этапом прогнозирования социально-экономических явлений является оценка точности и надежности прогнозов.
Эмпирической мерой точности прогноза, служит величина его ошибки, которая определяется как разность между прогнозными (  ) и фактическими (уt) значениями исследуемого показателя. Данный подход возможен только в двух случаях:
) и фактическими (уt) значениями исследуемого показателя. Данный подход возможен только в двух случаях:
а) период упреждения известен, уже закончился и исследователь располагает необходимыми фактическими значениями прогнозируемого показателя;
б) строится ретроспективный прогноз, то есть рассчитываются прогнозные значения показателя для периода времени за который уже имеются фактические значения. Это делается с целью проверки разработанной методики прогнозирования.
В данном случае вся имеющаяся информация делится на две части в соотношении 2/3 к 1/3. Одна часть информации (первые 2/3 от исходного временного ряда) служит для оценивания параметров модели прогноза. Вторая часть информации (последняя 1/3 части исходного ряда) служит для реализации оценок прогноза.
Полученные, таким образом, ретроспективно ошибки прогноза в некоторой степени характеризуют точность предлагаемой и реализуемой методики прогнозирования. Однако величина ошибки ретроспективного прогноза не может в полной мере и окончательно характеризовать используемый метод прогнозирования, так как она рассчитана только для 2/3 имеющихся данных, а не по всему временному ряду.
В случае если, ретроспективное прогнозирование осуществлять по связным и многомерным динамическим рядам, то точность прогноза, соответственно, будет зависеть от точности определения значений факторных признаков, включенных в многофакторную динамическую модель, на всем периоде упреждения. При этом, возможны следующие подходы к прогнозированию по связным временным рядам: можно использовать как фактические, так и прогнозные значения признаков.
Все показатели оценки точности статистических прогнозов условно можно разделить на три группы:
- аналитические;
- сравнительные;
- качественные.
Аналитические показатели точности прогноза позволяют количественно определить величину ошибки прогноза. К ним относятся следующие показатели точности прогноза:
Абсолютная ошибка прогноза (D*) определяется как разность между эмпирическим и прогнозным значениями признака и вычисляется по формуле:
 , (16.1)
, (16.1)
где уt – фактическое значение признака;
 - прогнозное значение признака.
- прогнозное значение признака.
Относительная ошибка прогноза (d*отн) может быть определена как отношение абсолютной ошибки прогноза (D*):
- к фактическому значению признака (уt):
 (16.2)
(16.2)
- к прогнозному значению признака (  )
)
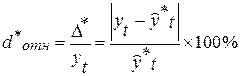 (16.3)
(16.3)
Абсолютная и относительная ошибки прогноза являются оценкой проверки точности единичного прогноза, что снижает их значимость в оценке точности всей прогнозной модели, так как на изучаемое социально-экономическое явление подвержено влиянию различных факторов внешнего и внутреннего свойства. Единично удовлетворительный прогноз может быть получен и на базе реализации слабо обусловленной и недостаточно адекватной прогнозной модели и наоборот – можно получить большую ошибку прогноза по достаточно хорошо аппроксимирующей модели.
Поэтому на практике иногда определяют не ошибку прогноза, а некоторый коэффициент качества прогноза (Кк), который показывает соотношение между числом совпавших (с) и общим числом совпавших (с) и несовпавших (н) прогнозов и определяется по формуле:
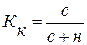 (16.4)
(16.4)
Значение Кк = 1 означает, что имеет место полное совпадение значений прогнозных и фактических значений и модель на 100% описывает изучаемое явление. Данный показатель оценивает удовлетворительный вес совпавших прогнозных значений в целом по временному ряду и изменяющегося в пределах от 0 до 1.
Следовательно, оценку точности получаемых прогнозных моделей целесообразно проводить по совокупности сопоставлений прогнозных и фактических значений изучаемых признаков.
Средним показателем точности прогноза является средняя абсолютная ошибка прогноза (  ), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:
), которая определяется как средняя арифметическая простая из абсолютных ошибок прогноза по формуле вида:
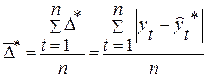 , (16.5)
, (16.5)
де n – длина временного ряда.
Средняя абсолютная ошибка прогноза показывает обобщенную характеристику степени отклонения фактических и прогнозных значений признака и имеет ту же размерность, что и размерность изучаемого признака.
Для оценки точности прогноза используется средняя квадратическая ошибка прогноза, определяемая по формуле:
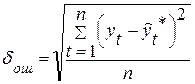 (16.6)
(16.6)
Размерность средней квадратической ошибки прогноза также соответствует размерности изучаемого признака. Между средней абсолютной и средней квадратической ошибками прогноза существует следующее примерное соотношение:
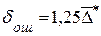 (16.7)
(16.7)
Недостатками средней абсолютной и средней квадратической ошибками прогноза является их существенная зависимость от масштаба измерения уровней изучаемых социально-экономических явлений.
Поэтому на практике в качестве характеристики точности прогноза определяют среднюю ошибку аппроксимации, которая выражается в процентах относительно фактических значений признака, и определяется по формуле вида:
 (16.8)
(16.8)
Данный показатель является относительным показателем точности прогноза и не отражает размерность изучаемых признаков, выражается в процентах и на практике используется для сравнения точности прогнозов полученных как по различным моделям, так и по различным объектам. Интерпретация оценки точности прогноза на основе данного показателя представлена в следующей таблице:
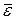 ,% ,%
| Интерпретация точности |
| < 10 10 – 20 20 – 50 > 50 | Высокая Хорошая Удовлетворительная Не удовлетворительная |
В качестве сравнительного показателя точности прогноза используется коэффициент корреляции между прогнозными и фактическими значениями признака, который определяется по формуле:
 , (16.9)
, (16.9)
где  - средний уровень ряда динамики прогнозных оценок.
- средний уровень ряда динамики прогнозных оценок.
Используя данный коэффициент в оценке точности прогноза следует помнить, что коэффициент парной корреляции в силу своей сущности отражает линейное соотношение коррелируемых величин и характеризует лишь взаимосвязь между временным рядом фактических значений и рядом прогнозных значений признаков. И даже если коэффициент корреляции R = 1, то это еще не предполагает полного совпадения фактических и прогнозных оценок, а свидетельствует лишь о наличии линейной зависимости между временными рядами прогнозных и фактических значений признака.
Одним из показателей оценки точности статистических прогнозов является коэффициент несоответствия (КН), который был предложен Г. Тейлом и может рассчитываться в различных модификациях:
1. Коэффициент несоответствия (КН1), определяемый как отношение средней квадратической ошибки к квадрату фактических значений признака:
 (16.10)
(16.10)
КН = о, если  , то есть полное совпадение фактических и прогнозных значений признака.
, то есть полное совпадение фактических и прогнозных значений признака.
КН = 1, если при прогнозировании получают среднюю квадратическую ошибку адекватную по величине ошибке, полученной одним из простейших методов экстраполяции неизменности абсолютных цепных приростов.
КН > 1, когда прогноз дает худшие результаты, чем предположение о неизменности исследуемого явления. Верхней границы коэффициент несоответствия не имеет.
2.Коэффициент несоответствия КН2 определяется как отношение средней квадратической ошибки прогноза к сумме квадратов
отклонений фактических значений признака от среднего уровня исходного временного ряда за весь рассматриваемый период:
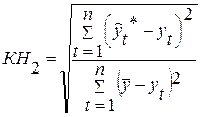 , (16.11)
, (16.11)
где  - средний уровень исходного ряда динамики.
- средний уровень исходного ряда динамики.
Если КН > 1, то прогноз на уровне среднего значения признака дал бы лучший результат, чем имеющийся прогноз.
3.Коэффициент несоответствия (КН3), определяемый как отношение средней квадратической ошибке прогноза к сумме квадратов отклонений фактических значений признака от теоретических, выравненных по уравнению тренда:
 , (16.12)
, (16.12)
где 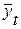 - теоретические уровни временного ряда, полученные по
- теоретические уровни временного ряда, полученные по
модели тренда.
Если КН > 1, то прогноз методом экстраполяции тренда дает хороший результат.
Виды степенных средних
| Вид степенной средней | Формула расчета | |
| простая | взвешенная | |
| Арифметическая | 
| 
|
| Гармоническая | 
|  где где  = = 
|
| Геометрическая | 
| 
|
| Квадратическая | 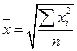
| 
|
| Кубическая | 
| 
|
В интервальном вариационном ряду для расчета средней арифметической взвешенной определяются и используются значения середины интервалов.
Рассмотрим методологию применения разных видов степенных средних на основе расчета средней заработной платы по двум предприятиям вместе: за январь, февраль и за два месяца. Исходные данные представлены в табл. 5.
Таблица 5
| № предприятия | Январь | Февраль | ||
| Средняя заработная плата, руб. | Численность работников, человек | Средняя заработная плата, руб. | Фонд оплаты труда, тыс. руб. | |
| 4 900 | 5 700 | 2 565 | ||
| 5 400 | 5 800 | 3 480 |
Определим исходные соотношения средней для показателя «средняя заработная плата»:

За январь мы располагаем данными о средней заработной плате и численности работников, т.е. нам известен знаменатель исходного соотношения, но неизвестен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
 ,
,
где  -i-й вариант осредняемого признака,
-i-й вариант осредняемого признака,
 -вес i-ого варианта.
-вес i-ого варианта.
За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда, т.е. нам известен числитель исходного соотношения, но неизвестен знаменатель. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда средняя заработная плата в целом по двум предприятиям будет рассчитываться по формуле
 ,
,
где  .
.
За два месяца средняя заработная плата по двум предприятиям определяется по формуле средней арифметической простой (невзвешенной), так как веса (f) отсутствуют или равны.
 (руб.),
(руб.),
где n-число единиц или объем совокупности.
Таким образом, исходя из приведенных данных, были применены разные виды степенных средних.
Средняя геометрическая используется в анализе динамики для определения среднего темпа роста.
Средняя квадратическая и степенные средние более высоких порядков используются при расчете ряда статистических показателей, характеризующих вариацию и взаимосвязь.
6. ПОКАЗАТЕЛИ ВАРИАЦИИ
6.1. ПОНЯТИЕ ВАРИАЦИИ. РАСЧЕТ СРЕДНЕГО ЛИНЕЙНОГО ОТКЛОНЕНИ
Различие в индивидуальных значениях признака внутри изучаемой совокупности в статистике называется вариацией признака.
Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.
Средняя величина – это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены они вблизи или значительно отклоняются от нее.
В тех случаях, когда отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, средняя хорошо представляет всю совокупность. В тех же случаях, когда отдельные значения совокупности далеко отстают от средней, средняя плохо представляет всю совокупность.
Колебания отдельных значений характеризуют показатели вариации. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием различных факторов. Различают случайную и систематическую вариации признака.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих его факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц х, к средней измеряется рядом абсолютных, средних и относительных показателей.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колебания признака используется ряд показателей. Наиболее простой из них – размах вариации.
Размах вариации (R) – это разность между наибольшим (хтах) и наименьшим (xmin) значениями вариантов

Пример 1. Имеются следующие данные об объемах товарооборота предприятий.
| Группы предприятий по объему товарооборота, млн руб. | Число предприятий |
| 90-100 | |
| 100-110 | |
| 110-120 | |
| 120-130 | |
| Итого |
Определяем показатель размаха вариации: R = 130 - 90 = 40 (млн руб.).
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариантов в ряду.
Для того чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений от средней без учета знака этих отклонений:

Порядок расчета среднего линейного отклонения следующий:
1) по значениям признака исчисляется средняя арифметическая:

2) определяются отклонения каждого вариантах xi, от средней: xi-x;
3) рассчитывается сумма абсолютных величин отклонений: 
4) сумма абсолютных величин отклонений делится на число значений 
Пример 2. Имеются следующие данные о производительности рабочих.
| Табельный номер рабочего | xi-x | |xi-x| | |
| -8 | |||
| -7 | |||
| Итого |
Рассчитаем среднее линейное отклонение:
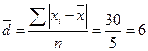
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная: 
2) определяются абсолютные отклонения вариантов от средней: 
3) полученные отклонения умножаются на частоты: 
4) находится сумма взвешенных отклонений без учета знака: 
5) сумма взвешенных отклонений делится на сумму частот: 
6 . 2. РАСЧЕТ ДИСПЕРСИИ И СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ПО ИНДИВИДУАЛЬНЫМ ДАННЫМ И В РЯДАХ РАСПРЕДЕЛЕНИЯ
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается а2. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
 дисперсия невзвешенная (простая);
дисперсия невзвешенная (простая);
 дисперсия взвешенная.
дисперсия взвешенная.
Среднее квадратическое отклонение – это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается 
 среднее квадратическое отклонение невзвешенное
среднее квадратическое отклонение невзвешенное
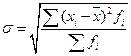 среднее квадратическое отклонение взвешенное.
среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенной следующий:
1) определяют среднюю арифметическую взвешенную:  ;
;
2) рассчитывают отклонения вариантов от средней: 
3) возводят в квадрат отклонение каждого варианта от средней:  ;
;
4) умножают квадраты отклонений на веса (частоты): 
5) суммируют полученные произведения: 
6) полученную сумму делят на сумму весов: 
Пример 3. Имеются следующие данные о производительности труда рабочих.
| Произведено продукции одним рабочим, шт. (Xj варианта) | Число рабочих, человек
(  ) )
| 
| 
| 
| 
|
| -2 | |||||
| -1 | |||||
| Итого |
Исчислим среднюю арифметическую взвешенную:

Значения отклонений от средней и их квадратов представлены в таблице.
Определим дисперсию: 
Среднее квадратическое отклонение будет равно
 (шт.)
(шт.)
Если исходные данные представлены в виде интервального ряда распределения, то сначала нужно определить дискретное значение признака, а затем применить изложенный метод.
Пример 4. Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы.
| Урожайность пшеницы, ц/га | Посевная площадь, га ( 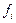 ) )
| 
|  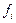
| 
| 
| 
|
| 14-16 | -3,4 | 11,56 | ||||
| 16-18 | -1,4 | 1,96 | ||||
| 18-20 | 0,6 | 0,36 | ||||
| 20-22 | 2,6 | 6,76 | ||||
| Итого |
Средняя арифметическая равна
 (ц/га)
(ц/га)
Вычислим дисперсию:  .
.
6.3. РАСЧЕТ ДИСПЕРСИИ ПО ФОРМУЛЕ ПО ИНДИВИДУАЛЬНЫМ ДАННЫМ И В РЯДАХ РАСПРЕДЕЛЕНИЯ
Техника вычисления дисперсии сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Дисперсия имеет следующие свойства.
1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсию не изменяет.
2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсию не изменяет.
3. Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в k2 раз, а среднее квадратическое отклонение – в k раз.
4. Дисперсия признака относительно произвольной величины(  ) всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:
) всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:  . Если А = 0, то приходим к следующему равенству:
. Если А = 0, то приходим к следующему равенству:  , т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими. Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую: 
2) возводят в квадрат среднюю арифметическую: 
3) возводят в квадрат отклонение каждого варианта ряда: x2i;
4) находят сумму квадратов вариантов:  ;
;
5) делят сумму квадратов вариантов на их число, т.е. определяют средний квадрат: 
6) определяют разность между средним квадратом признака и квадратом средней: 
Пример 5. Имеются следующие данные о производительности труда рабочих.
| Табельный номер рабочего | Произведено продукции, шт. (xi) | xi2 |
| Итого |
Произведем следующие расчеты:
 (шт.)
(шт.)

Рассмотрим расчет дисперсии в интервальном ряду распределения. Порядок расчета дисперсии взвешенной (по формуле  ) следующий:
) следующий:
1) определяют среднюю арифметическую: 
2) возводят в квадрат полученную среднюю:  ;
;
3) возводят в квадрат каждый вариант ряда:  ;
;
4) умножают квадраты вариантов на частоты: 
5) суммируют полученные произведения: 
6) делят полученную сумму на сумму весов и получают средний
квадрат признака: 
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию: 
6.4. ПОКАЗАТЕЛИ ОТНОСИТЕЛЬНОГО РАССЕИВАНИЯ
Для характеристики меры изменения изучаемого признака исчисляются показатели изменения в относительных величинах.
Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Показатель меры относительного рассеивания рассчитывается как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции (Ко) отражает относительное изменение крайних значений признака вокруг средней:

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

3. Коэффициент вариации (V):

Поскольку среднеквадратическое отклонение дает обобщающую характеристику изменяемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Исходят из того, что если V больше 40%, то это говорит о большой колеблемости признака в изучаемой совокупности.
6.5. ПОКАЗАТЕЛИ ХАРАКТЕРИСТИКИ ВАРИАЦИОННЫХ РЯДОВ
Наряду со средней арифметической в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, средняя гармоническая может быть простой и взвешенной.
Характеристиками вариационных рядов наряду со средними являются мода и медиана.
Мода – это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Для интервальных рядов распределения с равными интервалами мода (Мо) определяется
по формуле

где  начальное значение интервала, содержащего моду
начальное значение интервала, содержащего моду
 – величина модального интервала;
– величина модального интервала;
 – частота модального интервала;
– частота модального интервала;
 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Медиана – это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд – это расположение единиц совокупности в возрастающем или убывающем порядке).
7.1. ПОНЯТИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ
Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге.
Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения может быть построен по непрерывно варьирующему признаку (признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения).
Анализ рядов распределения осуществляется с помощью следующих показателей (показатели центра распределения).
Средняя арифметическая взвешенная (  ):
):  ,
,
где  - середина интервала:
- середина интервала: 
 и
и  – нижняя и верхняя границы интервалов соответственно.
– нижняя и верхняя границы интервалов соответственно.
Медиана (Me) – середина ранжированного ряда.
В интервальном вариационном ряду медиана рассчитывается по формуле  ,
,
где  , – нижняя граница медианного интервала; h- ширина интервала, SMe-1 – накопленная частота интервала, предшествующего медианному, fMe – частота медианного интервала.
, – нижняя граница медианного интервала; h- ширина интервала, SMe-1 – накопленная частота интервала, предшествующего медианному, fMe – частота медианного интервала.
Мода (Мо) – наиболее часто встречающееся значение признака в совокупности.
В интервальном вариационном ряду мода находится в интервале с максимальной частотой и рассчитывается по формуле, которую мы уже приводили:

где  – нижняя граница модального интервала;
– нижняя граница модального интервала;  – частота модального интервала;
– частота модального интервала;  – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;  – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
7.2. ПОНЯТИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ
Большое значение при изучении социально-экономических процессов и явлений имеет графическое изображение статистической информации. Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой. Графический метод широко применяется для иллюстрации происходящих социально-экономических процессов и явлений.
Применение графиков в статистике насчитывает более чем двухсотлетнюю историю. Основоположником графического метода в статистике коммерческой деятельности считают английского экономиста У. Плейфейра (1731-1798). В своих работах он впервые применил способы графического изображения статистических данных (линейные, столбиковые, секторные и другие диаграммы).
Статистические графики – это одно из самых наглядных средств представления информации.
Статистический график представляет собой чертеж, на котором при помощи условных геометрических фигур изображаются статистические данные. В результате этого получается наглядная характеристика изучаемой статистической совокупности.
Статистический график состоит из следующих основных элементов:
■ поле графика;
■ графический образ;
■ пространственные и масштабные ориентиры;
■ экспликация графика.
Поле графика представляет собой место, на котором график выполняется. Это листы бумаги, географические карты, план местности и т.п. Поле графика характеризуется его форматом (размерами и пропорциями сторон). Размер поля графика зависит от его назначения.
Графический образ – это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольники, квадраты, круги и т.д.). В качестве графического образа выступают и объемные фигуры. Иногда в графиках используются негеометрические фигуры в виде силуэтов или рисунков предметов.
Пространственные ориентиры определяют размещение графических образов на поле графика. Эти ориентиры задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значениям изучаемых показателей.
Масштабные ориентиры статистического графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал.
Масштаб графика – это мера перевода численной величины в графическую (например, 1 см соответствует 100 тыс. руб.); чем длиннее отрезок линии, принятой за числовую единицу, тем крупнее масштаб.
Масштабной шкалой является линия, отдельные точки которой читаются как определенные числа. Шкала, по которой отсчитываются уровни изучаемых показателей, как правило, начинается с нуля. Последнее число, наносимое на шкалу, несколько превышает максимальный уровень, отсчет которого проводится по этой шкале. При построении графика допускается разрыв масштабной шкалы. Этот прием используется для изображения статистических данных, имеющих значения лишь в определенных значениях.
Экспликация графика – это пояснение его содержания. Экспликация включает в себя заголовок графика, объяснения масштабных шкал, пояснения отдельных элементов графического образа.
Заголовок графика в краткой и четкой форме отражает основное содержание изображаемых данных. Помимо заголовка на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения.
7.3. КЛАССИФИКАЦИЯ СТАТИСТИЧЕСКИХ ГРАФИКОВ
При всем своем многообразии статистические графики в курсе «Статистика» классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.
По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.
Диаграмма представляет собой чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков.
Диаграмма сравнения показывает соотношение признака статистической совокупности. Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков определяется числом изучаемых показателей (данных). Расстояние между столбиками должно быть одинаковым. У основания столбиков дается название изучаемого показателя.
Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально удельному весу отображаемых частей целого
Статистическая карта – вид графика, который иллюстрирует содержание статистических таблиц, где подлежащим является административное или географическое деление совокупности. На лист изображения наносится контурная географическая карта, отражающая деление совокупности на группы. Статистическая карта называется картограммой, вся информация на ней отображается в виде штриховки, линий, точек, окраски, отражающих изменение какого-либо показателя.
На картодиаграмме на фоне карты присутствуют элементы диаграммных фигур. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.
При обработке и отображении экспериментальных данных, в которых изучаемый признак может принимать любое значение из некоторого интервала, используют следующие способы представления данных:
■ гистограмма;
■ полигон частот;
■ полигон накопленных частот (кумулята).
Гистограмма состоит из примыкающих друг к другу прямоугольников, изображенных на координатной сетке.
Полигон частот – ломаная линия, соединяющая точки, соответствующие срединным значениям интервалов группировки и частотам интервалов.
Полигон частот получается из гистограммы, если соединить середины вершин прямоугольников ломаной линией.
Полигон накопительных частот. В данном случае для построения используются накопленные частоты.
ТРЕБОВАНИЯ К ПОСТРОЕНИЮ СТАТИСТИЧЕСКИХ ГРАФИКОВ
Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс.
Общим требованием графического метода изображения статистических показателей является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки – по вертикальной шкале и читаются снизу вверх. Это повышает аналитическое значение статистических графиков. Важно, чтобы заголовок графика был бы кратким, но достаточно четко пояснял основное его содержание.
8.1. ПОНЯТИЕ И КЛАССИФИКАЦИЯ РЯДОВ ДИНАМИКИ
Ряды динамики – это статистические данные, отображающие развитие изучаемого явления во времени.
Ряд динамики состоит из двух элементов: в нем указываются моменты времени (обычно дата) или периоды времени (год, квартал, месяц, сутки), к которым относятся приводимые статистические данные и статистические показатели – уровни ряда, характеризующие состояние явления на указанный момент или за период.
Ряды динамики классифицируют следующим образом.
1.В зависимости от способа выражения уровней различают ряд абсолютных величин, ряд средних величин, ряд относительных величин.
2.В зависимости от того, как уровни ряда отражают состояние явления: на определенные моменты времени (начало месяца, квартала, года и т.п.) или за определенные интервалы времени (за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики.
3.В зависимости от расстояния между уровнями ряды динамики могут быть с равноотстоящими уровнями и неравно отстоящими уровнями во времени.
4.В зависимости от наличия основной тенденции изучаемого процесса ряды динамики бывают стационарными и нестационарными.
5.По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики.
Сопоставимость уровней рядов динамики. Уровни ряда динамики должны быть сопоставимы по методологии учета и расчета показателей, территориальным границам, кругу охватываемых объектов, единицам измерения и другим признакам. В тех случаях, когда уровни ряда динамики оказываются несопоставимы между собой, их необходимо привести к сопоставимому виду, применяя прием, который называют смыканием рядов динамики.
Для количественной оценки динамики социально-экономических явлений применяются следующие статистические показатели: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Средние показатели ряда динамики являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики.
Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
Выявление основной тенденции ряда динамики. При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы: метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания.
Наиболее эффективный метод выявления основной тенденции развития – аналитическое выравнивание. В этом случае уровни ряда динамики выражаются в виде функции времени: yt = f(t).
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Функция выбирается на основе анализа характера закономерности динамики данного явления.
Колеблемость динамических рядов. Основная тенденция показывает, как систематические факторы воздействуют на уровень ряда динамики, а колеблемость уровней тренда служит мерой воздействия остаточных факторов.
Мерой колеблемости динамического ряда выступает средний квадрат отклонений фактических уровней, исчисленных по тренду. Ее можно измерить показателем среднего квадратического отклонения.
Относительной мерой колеблемости является коэффициент вариации, равный отношению среднего квадратического отклонения к среднему уровню ряда.
Измерение сезонных колебаний. При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по инутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или несколько лет. При изучении сезонных колебаний используются специальные показатели – индексы сезонности (Is):

где  – средняя для каждого месяца за изучаемый период;
– средняя для каждого месяца за изучаемый период;
 – общий средний месячный уровень за изучаемый период.
– общий средний месячный уровень за изучаемый период.
Совокупность исчисленных для каждого годового цикла индексов сезонности характеризует сезонную волну развития явления во внутригодовой динамике и наглядно может быть представлена графическим методом. При наличии ярко выраженной тенденции развития (увеличение или уменьшение уровней из года в год) применимы другие способы измерения сезонных колебаний, в частности, индексы сезонности определяются на основе методов, которые позволяют исключать влияние тенденции роста (падения).
В таких случаях фактические данные сопоставляются с выравненными, и индексы сезонности определяются по формуле

где  – исходные уровни ряда;
– исходные уровни ряда;
 – выравненные (теоретические) уровни ряда; п – число годовых периодов.
– выравненные (теоретические) уровни ряда; п – число годовых периодов.
Выравнивание может быть проведено методом аналитического выравнивания или методом скользящей средней.
8.2. СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ
Пример 1. Имеются следующие данные о динамике производства тканей в одном из регионов за 1999–2003 гг.
| Год | Производство тканей, млн м2 | Абсолютный прирост, млн м2 | Темп роста, % | Темп прироста, % | Абсолютное значение | ||||
| по сравнению с предыдущим годом | по сравнению с 1999 г. | по сравнению с предыдущим годом | по сравнению с 1999 г. | 1% прироста, млн м2 | |||||
| по сравнению с предыдущим годом | по сравнению с 1999 г. | ||||||||
| - | - | - | 100,0 | - | - | - | |||
| 104,3 | 104,3 | 4,3 | 4,3 | 2,56 | |||||
| 104,5 | 109,0 | 4,5 | 9,0 | 2,67 | |||||
| 104,3 | 113,7 | 4,3 | 13,7 | 2,79 | |||||
| 104,8 | 119,1 | 4,8 | 19,1 | 2,91 | |||||
| Итого | - | - | - | - | - | - |
Аналитические показатели уровня ряда получаются сравнением уровней между собой.
Сравниваемый уровень принято называть текущим, а уровень, с которым происходит сравнение,– базисным. За базу сравнения обычно принимают предыдущий уровень или начальный уровень ряда динамики.
При сравнении каждого уровня с предыдущим получаются цепные показатели.
Если же сравнение ведется с одним уровнем (базой), то показатели называются базисными.
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост ( 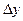 ). Его величина определяется как разность двух сравниваемых уровней и вычисляется следующим образом:
). Его величина определяется как разность двух сравниваемых уровней и вычисляется следующим образом:
 – базисные показатели;
– базисные показатели;
 – цепные показатели,
– цепные показатели,
где  – уровень i-го периода (кроме первого); у0 – уровень базисного периода;
– уровень i-го периода (кроме первого); у0 – уровень базисного периода;  – уровень предыдущего периода.
– уровень предыдущего периода.
В примере 1 абсолютный прирост по сравнению с 1999 г. составит:
■ в 2000 г.-Dy= 267 - 256= 11 (млн м2);
■ в 2001 г. - Dy - 279 - 256 = 23 (млн м2) и т.д.
Цепные показатели абсолютного прироста для примера 1. Абсолютный прирост составит:
■ в 2000 г. по сравнению с 1999 г.- Dy = 267 - 256 = 11 (млн м2);
■ 2001 г. по сравнению с 2000 г. - Dy = 279 - 267 = 12 (млн м2) и т.д.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному.
Этот показатель называется коэффициентом роста, или темпом роста (Гр), и выражается в процентах:
 – базисные показатели;
– базисные показатели;
 – цепные показатели.
– цепные показатели.
Если Тр больше 100%, уровень растет, если меньше - уровень уменьшается. Тр – всегда положительное число. В примере 1 темп роста составит:
■ в 2000 г. по сравнению с базисным 1999 г. – 
■ в 2001 г. по сравнению с базисным 1999 г. –  и т.д.
и т.д.
Рассчитаем цепные показатели темпа роста для примера 1. Темп роста составит:
■ в 2000 г. по сравнению с базисным 1999 - 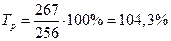
■ в 2001 г. по сравнению с 2000 г. – 
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Тпр), который рассчитывается как отношение абсолютного прироста к базисному или предыдущему уровню:
 – базисные показатели;
– базисные показатели;
 – цепные показатели.
– цепные показатели.
Показатель абсолютного значения 1% прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах.
 , или
, или  .
.
В примере 1 абсолютное значение прироста 1% составит:
■ в 2000 г. по сравнению с 1999 г. -  (млн. м2);
(млн. м2);
■ в 2001 г. по сравнению с 2000 г. -  (млн. м2) и т.д.
(млн. м2) и т.д.
8.3. МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ
Покажем применение скользящей средней на следующем примере.
Пример 4. На основе данных об урожайности зерновых культур в хозяйстве за 1989–2003 гг. проведем сглаживание ряда методом скользящей средней.
Динамика урожайности зерновых культур в
хозяйстве за 1989–2003 гг. и расчет скользящих средних
| Год | Урожайность зерновых, ц/га | Трехлетние скользящие суммы | Трехлетние скользящие средние | 4-летние скользящие суммы | 4-летние скользящие средние (нецентри- рованные) | 4-летние скользящие средние (центри- рованные) |
| 19,5 | - | - | - | - | - | |
| 23,4 | - | 22,6 | - | 22,5 | - | |
| 25,0 | 67,9 | 23,6 | - | 24,1 | 23,3 | |
| 22,4 | 70,8 | 24,3 | 90,3 | 25,4 | 24,8 | |
| 25,5 | 72,9 | 25,6 | 96,3 | 25,8 | 25,6 | |
| 28,8 | 76,7 | 27,0 | 101,7 | 27,8 | 26,8 | |
| 26,6 | 80,9 | 28,6 | 103,3 | 26,6 | 27,2 | |
| 30,4 | 85,8 | 25,9 | 111,3 | 28,4 | 27,5 | |
| 20,7 | 77,7 | 29,0 | 106,5 | 30,7 | 26,6 | |
| 35,8 | 86,9 | 30,8 | 113,5 | 29,5 | 30,3 | |
| 36,0 | 92,5 | 32,5 | 122,9 | 32,5 | 31,0 | |
| 25,6 | 97,4 | 31,4 | 118,1 | 32,3 | 32,4 | |
| 32,5 | 94,1 | 31,0 | 129,9 | 30,1 | 31,2 | |
| 35,0 | 94,7 | 31,6 | 129,1 | - | - | |
| 27,2 | 94,7 | - | 120,3 | - | - |
По графе 5 значения показателей находятся в промежутке между годами
Суть метода скользящей средней состоит в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из того же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Средняя из нечетного числа уровней относится к середине интервала. Если интервал сглаживания четный, то отнесение средней к определенному времени невозможно, она относится к середине между датами. Для того чтобы правильно отнести среднюю из четного числа уровней, применяется центрирование, т.е. нахождение средней из средней, которую относят уже к определенной дате.
1. Рассчитаем трехлетние скользящие суммы. Пример 4(окончание).
Находим сумму урожайности за 1989–1991 гг.: 19,5 + 23,4 + 25,0 = = 67,9 и записываем это значение в 1991 г. Затем из этой суммы вычитаем значение показателя за 1989 г. и прибавляем показатель за 1992 г.: 67,9 - 19,5 + 22,4 = 70,8 и это значение записываем в 1992 г. и т.д.
2. Определим трехлетние скользящие средних по формуле простой
средней арифметической:

Полученное значение записываем в 1990 г. Затем берем следующую трехлетнюю скользящую сумму и находим трехлетнюю скользящую среднюю: 70,8 : 3 = 23,6, полученное значение записываем в 1991 г. и т.д.
Аналогичным образом рассчитываются четырехлетние скользящие суммы. Их значения представлены в графе 4 таблицы данного примера.
Четырехлетние скользящие средние определяются по формуле простой средней арифметической:

Это значение будет отнесено между двумя годами –1990 и 1991 гг., т.е. в середине интервала сглаживания. Для того чтобы найти четырехлетние скользящие средние центрированные, необходимо найти среднюю из двух смежных скользящих средних:

Эта средняя будет отнесена к 1991 г. Аналогичным образом рассчитываются остальные центрированные средние; их значения записываются в графу 6 таблицы данного примера.
9.1. ПОНЯТИЕ ИНДЕКСОВ. ИХ ВИДЫ
Индексы – важнейший обобщающий показатель. С их помощью можно измерить динамику социально-экономического явления за два или более периодов времени, динамику среднего показателя и сопоставить уровни явления в пространстве, по странам, экономическим районам, областям и т.д. Индексы используются для определения степени влияния изменений значений одних показателей на динамику других, а также для пересчета значений макроэкономических показателей из фактических цен в сопоставимые.
Простейший показатель, применяемый в индексном анализе,– индивидуальный индекс, который характеризует изменение во времени или в пространстве отдельных однородных элементов совокупности. Например, индивидуальные индексы физического объема продукции, цен, себестоимости единицы продукции.
В экономических расчетах чаще всего используются сводные, или общие, индексы, которые характеризуют изменение совокупности в целом.
Построение этих индексов является содержанием индексной методологии, в которой сложились две концепции: синтетическая и аналитическая.
Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных явлений, отдельные части которых непосредственно несоизмеримы, и поэтому индексы – показатели синтетические.
В соответств
Дата добавления: 2014-12-23; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |