Механическая энергия и динамика частицы

Итак, с одной стороны, нами найдена искомая специфическая характеристика объекта – темп изменения импульса со временем, которая чувствительно реагирует на внешнее воздействие. С другой стороны, обнаружена новая величина – сила F воздействия окружения на объект, с помощью которой мы имеем возможность мысленно заместить наличие окружения, влияющего на объект. Из независимых экспериментов мы смогли также установить законы для некоторых конкретных сил. Как же следует воспользоваться накопленным багажом, чтобы на этой основе научиться предсказывать закономерности поведения физических характеристик несвободной частицы?

Сначала выделим из них базисные характеристики. Нетрудно видеть, что это радиус – вектор r и импульс р, поскольку через эти две характеристики можно выразить все другие характеристики частицы и ее окружения. Кроме того, эти характеристики являются независимыми друг от друга, поскольку для полного описания движения частицы по траектории необходимо задать как положение частицы на траектории, так и ее скорость. Дело в том, что они показывают, где в данный момент времени находится частица, куда она предполагает двигаться из данного пункта и с какой «прытью». Поэтому говорят, что эти характеристики совместно описывают состояние частицы в фиксированный момент времени. Иначе говоря, они представляют нам полную информацию о ее движении. Но это мгновенная информация и через какое-то время она может устареть. Так как же узнать, какими будут значения положения и скорости частицы в некий последующий, а лучше – в любой другой момент времени?

Прежде, чем приступить к изложению общего метода нахождения этих характеристик, сделаем очень важное замечание. Дело в том, что сила, вообще говоря, не является единственной и универсальной характеристикой воздействия на частицу. Если это воздействие осуществляется более массивным материальным объектом, который мы можем считать неподвижным, и имеет гравитационный, электрический или упругий характер, то в нашем распоряжении оказывается еще одна новая характеристика. В этих условиях она приписывается объекту (более легкой частице), потому что формально зависит только от ее координат, хотя на самом деле она принадлежит всей системе в целом. Эта характеристика называется потенциальной энергией U(r), и поэтому даже соответствующие силы называют потенциальными. Конкретный вид зависимости U(r) определяется соответствующим законом силы. Так, для силы тяжести вблизи поверхности Земли на высоте h она равна mgh. Как оказалось, это действительно энергетическая характеристика, потому что она увеличивает способность тела производить работу. Достоинство потенциальной энергии состоит в том, что совместно с кинетической энергией она образует новую физическую величину – механическую энергию е_мех, которая, несмотря на внешнее воздействие, обладает свойством сохранения.

Итак, е_мех, равная сумме кинетической и потенциальной энергий для одной несвободной частицы, находящейся под влиянием потенциальных сил, остается неизменной величиной

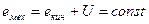(7.7).

При этом каждая из составляющих ее энергий по отдельности данным свойством в этих условиях не обладает. Здесь уместна следующая аналогия. День и ночь совместно образуют сутки, составляющие 24 часа, однако продолжительность дня и ночи, как известно, изменяется в зависимости от времени года. Факт сохранения емех (в тех обстоятельствах, когда ее можно ввести) облегчает решение целого ряда задач. Вместе с тем, отметим, что механическая энергия не относится к числу фундаментальных характеристик движения.

Обратимся теперь к общему случаю произвольного воздействия, описываемого силой. Ограничимся рассмотрением прямолинейного движения несвободной частицы (вдоль оси X). Тогда для предсказания поведения частицы в последующий момент времени в нашем распоряжении есть два соотношения. Одно из них – это определение скорости через импульс:

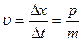(7.8).

Оно позволит, если нам известно значение импульса р, найти изменение положения частицы Dх через промежуток времени Dt:

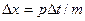(7.9).

Если нам к тому же известно значение координаты частицы х0 в некоторый начальный момент времени t0, то теперь, подставляя разные значения Dt, мы можем вычислять местонахождение частицы в любой момент времени 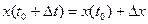. Но для этого нужно знать значение импульса, а он у несвободной частицы непостоянен. Поэтому, даже если мы можем проделать эту процедуру вычислений в момент времени Dt, очень близкий к началу движения, когда еще можно предположить, что импульс почти не успел измениться, то в последующие моменты времени ею пользоваться уже нельзя.

Проблему удается разрешить, поскольку известно, в каком окружении находится частица. Другими словами, мы знаем закон действующей на нее силы (например, силы упругости или любой другой). Тогда можно воспользоваться выражением, использованным еще Ньютоном в качестве определения силы, или (опуская символ предела 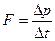, однако прочитав его иначе, т.е. вложив в него другой смысл. Ведь при известных F и Dt это выражение перестает быть определением силы, а становится средством вычисления Dр в виде: Dр = FDt.

Конечно, это еще не сам искомый импульс, но это его, изменение за время Dt, прошедшее с того момента t₀ когда импульс нам был определенно известен. Второй способ прочтения предыдущей формулы соответствует содержанию второго закона Ньютона, на основании которого мы сможем установить неизвестное нам пока, но очень необходимое значение импульса в любой момент времени t₀+Dt:

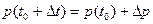(7.10).

Таким образом, зная значения координаты и импульса несвободной частицы в некоторый момент времени, можно воспользоваться двумя соотношениями, которые называются системой уравнений движения Ньютона, а также выражением для конкретного закона силы, чтобы найти значения положения и импульса частицы спустя любой промежуток времени после начала движения.

Соотношения, описывающие изменение координаты и импульса (или скорости) частицы со временем, называются законами движения. Они эквивалентны по своей значимости, так как одно может быть получено из другого. Так для равноускоренного движения с ускорением а они имеют вид

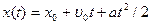(7.11),

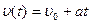(7.12).

Если же шарик массы m колеблется на пружинке под действием упругой силы, то закон движения имеют вид:

(7.13),

(7.14).

Такая система называется гармоническим осциллятором. В ней частица совершает гармонические колебания по закону синуса и косинуса, с периодом Т=2p/w, где 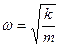– собственная частота колебаний. Соответственно величину А называют амплитудой колебаний, а j₀ – начальной фазой.

Итак, с помощью уравнений движения Ньютона мы можем отыскать законы движения частицы для координаты и скорости, а далее через них – законы движения и для других характеристик, например, импульса, энергии и т.д.

Высокая способность к точным предсказаниям будущих и прошлых значений координаты и скорости частицы можно продемонстрировать на многих примерах. Особенно сильное впечатление она производит в небесной механике, в которой на основе уравнений движения частицы удается предсказывать положения планет и комет на небесной сфере, а также время и место будущих и прошедших солнечных и лунных затмений.

Одной из убедительных демонстраций эффективности описания природы на основе модели несвободной частицы в середине XIX века явилось открытие планеты Нептун. Дело в том, что для более близкой к Солнцу планеты Уран уравнения движения давали не совсем точные предсказания ее положения и скорости. В связи с этим французский ученый Леверье, непоколебимо веривший в справедливость уравнений движения и всю схему механики Ньютона, предположил, что дело не в этих уравнениях, а в том, что в них учтены не все силы, действующие на планету Уран. Если же допустить, что на нее действует еще одна, неизвестная планета, то по закону всемирного тяготения ему удалось приближенно установить массу и положение этой планеты. Вскоре она действительно была открыта астрономами.