Критерий устойчивости Найквиста. Формула Найквиста

В своем рассмотрении теплового шума Найквист воспользовался приемом, заключающимся в анализе обмена энергией между двумя электрическими проводниками, соединенными идеальной передающей линией без потерь и находящимися в состоянии равновесия при температуре. Используя теорему о равнораспределении, согласно которой на каждую степень сво­боды приходится энергия hf.

Формула Найквиста широко используется при расчёте тепловых шумов в измерительных и радиотехнических устройствах. Она определяет величину тепловых флуктуаций тока или напряжения в электрической цепи. Получена формула американским физиком Х. Найквистом в 1928г.

Согласно ней, обусловленное тепловыми флуктуациями среднее значение квадрата напряжения на концах проводника с сопротивлением R, находящегося в состоянии теплового равновесия при абсолютной температуре Т, равно:

(17.1).

При низких температурах и достаточно высоких частотах, когда h ³ kT вместо формулы (1), следует пользоваться более общим выражением:

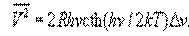(17.2).

Критерий Найквиста был разработан американским физиком Найквистом и опубликован в 1932 году. По постановке задачи он отличается от других критериев, будучи ориентирован на исследование устойчивости систем с обратной связью (замкнутых систем). Более конкретно критерий решает вопрос устойчивости замкнутой системы по заданной амплитудно-фазовой характеристике системы в разомкнутом состоянии. Данная постановка позволяет во многих случаях при исследовании устойчивости системы использовать исходные характеристики, не только заданные аналитически, но и полученные экспериментально. Для того чтобы судить об устойчивости замкнутой системы, исследователь должен иметь своем распоряжении амплитудно-фазовую характеристику (АФХ) разомкнутой системы, а также определенную информацию о распределении корней характеристического уравнения А(р)=0 разомкнутой системы. Варианты распределения корней характеристического уравнения обычно классифицируют, сводя к трем возможным случаям:

1. Разомкнутая система устойчива, то есть все корни полинома А(р) являются левыми.

2. Разомкнутая система неустойчива – полином А(р) имеет к правых корней и предполагается их отсутствие на мнимой оси.

3. Полином А(р) имеет корни на мнимой оси.