ВЗАИМОСВЯЗИ ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ

Вариант 1

1. Какая связь между факторным и результативным признаками называется криволинейной?

а) когда связь между факторным и результативным признаками можно представить в виде уравнения прямой;

б) когда связь между факторным и результативным признаками можно представить в виде уравнения параболы или гиперболы;

в) когда связь между факторным и результативным признаками функциональная.

2. Что означает параметр в однофакторной регрессионной модели ?

а) характеризует изменение факторного признака при изменении результативного на единицу измерения;

б) характеризует изменение результативного признака при изменении факторного признака на единицу измерения;

в) характеризует изменение результативного признака при изменении факторного на процент.

3. Какой из статистических методов применяется для выявления тенденции зависимости результативного признака от факторного признака?

а) табличный метод;

б) графический метод;

в) индексный метод.

Вариант 2

1. Какая связь между факторным и результативным признаками называется обратной?

а) когда с увеличением факторного признака результативный уменьшается;

б) когда с увеличением факторного признака результативный увеличивается;

в) когда с увеличением факторного признака результативный остается без изменения.

2. Какова методология расчета линейного коэффициента корреляции?

а) б) в)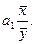

3. Какая связь между факторным и результативным признаками считается прямолинейной?

а) когда связь между факторным и результативным признаками можно представить в виде уравнения параболы;

б) когда связь между факторным и результативным признаками можно представить в виде уравнения гиперболы;

в) когда связь между факторным и результативным признаками можно представить в виде уравнения прямой.

Вариант 3

1. Когда связь между факторным и результативным признаками считается функциональной?

а) когда линейный коэффициент корреляции равен ± 1;

б) когда линейный коэффициент корреляции равен нулю;

в) когда линейный коэффициент корреляции больше нуля, но меньше +1.

2. Какова методология расчета коэффициента эластичности?

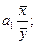а) б) в)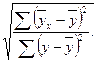

3. Что характеризует линейный коэффициент корреляции?

а) изменение результативного признака при изменении факторного признака на единицу измерения;

б) тесноту связи между факторным и результативным признаками;

в) изменение результативного признака при изменении факторного признака на один процент.

Вариант 4

1. Какая связь между факторным и результативным признаками называется прямой?

а) когда с увеличением факторного признака результативный увеличивается;

б) когда с увеличением факторного признака результативный уменьшается;

в) когда с увеличением факторного признака результативный остается без изменения.

2. Какие значения, принимаемые линейным коэффициентом корреляции являются необходимыми и достаточными?

а) от -1 до +1;

б) от 0 до +1;

в) от -1 до 0.

3. Какая связь между факторным и результативным признаками является корреляционной?

а) когда такую связь можно формализовать;

б) когда такую связь нельзя формализовать;

в) когда определяется влияние двух и более факторов на результативный признак.

Вариант 5

1. Какая связь между факторным и результативным признаками является функциональной?

а) когда такую связь нельзя формализовать;

б) когда такую связь можно формализовать;

в) когда связь будет прямая.

2. Какова методология расчета корреляционного отношения?

а) б) в)

3. В чем сущность корреляционного метода анализа?

а) выявление тесноты связи между факторным и результативным признаками;

б) определение аналитической формы связи между факторным и результативным признаками и установление тесноты связи между ними;

в) выявление тенденции развития экономических явлений.