
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример работы и обучения нейронной сети
Рассмотрим работу и обучение нейронной сети на примере. Дана сеть с 2 входами, двумя скрытыми слоями, в каждом из которых по 2 нейрона, и одним выходом. Функции активации нейронов – лог-сигмоидные (6.6), а = 1. Скорость обучения η примем равной 0,8. Необходимо реализовать с помощью ИНС логическую операцию «ИЛИ». Таблица истинности представлена в табл. 6.2, где x1 и x2 – входные переменные, а y – значение результата.
Табл. 6.2. Таблица истинности для операции «ИЛИ»
| x1 | x2 | y |
Предположим, что на некотором этапе обучения получена сеть, соответствующая изображенной на рис. 6.6. Допустим также, что на некотором шаге веса сети равны значениям из табл. 6.3. Смещения нейронов обозначены как веса с индексом «–».
Табл. 8.3. Веса связей ИНС
| Номер слоя | Индекс нейрона | Индекс веса | Вес |
| - | 0,02 | ||
| 0,12 | |||
| 0,35 | |||
| - | -0,015 | ||
| -0,5 | |||
| 0,24 | |||
| - | -0,084 | ||
| -0,33 | |||
| 0,27 | |||
| - | 0,037 | ||
| -0,08 | |||
| 0,79 | |||
| - | 0,04 | ||
| 0,062 | |||
| 0,64 |
Роль обучающей выборки в рассматриваемом случае играют данные из табл. 6.2, в которой каждая строка соответствует одному набору данных. Пусть на вход нейронной сети поданы входные сигналы из 2-го обучающего набора (x1 = 0, x2 = 1). Тогда, в соответствии с таблицей истинности (табл. 6.2), выход сети должен равняться 1. Действительные значения выходов нейронов приведены в табл. 6.4. На рис. 6.13, поясняется вычисление выходных сигналов ИНС.
Табл. 6.4. Значения выходных
сигналов нейронов
| Номер слоя | Индекс нейрона | Значение выхода |
| 0,591 | ||
| 0,556 | ||
| 0,468 | ||
| 0,606 | ||
| 0,612 |
Требуемое значение выхода сети «1», следовательно ошибка сети на данном этапе равна:
Е2 = 0,5 * (1 – 0,612)2 = 0,075.

Рис. 6.13. Прямой проход для вычисления выхода ИНС
Ошибка выходного нейрона, согласно (6.5.8):
 = 0,612 * (1 – 0,612) * (0,612 – 1) = – 0,092.
= 0,612 * (1 – 0,612) * (0,612 – 1) = – 0,092.
Ошибки нейронов 2 скрытого слоя по формуле (6.5.9):
 = 0,468 * (1 – 0,468) * (– 0,092) * 0,062 = – 0,001,
= 0,468 * (1 – 0,468) * (– 0,092) * 0,062 = – 0,001,
 = 0,606 * (1 – 0,606) * (– 0,092) * 0,64 = – 0,014.
= 0,606 * (1 – 0,606) * (– 0,092) * 0,64 = – 0,014.
Ошибки нейронов 1 скрытого слоя по формуле (6.5.9):
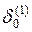 = 0,591 * (1 – 0,591) * ((– 0,001) * ( – 0,33) +
= 0,591 * (1 – 0,591) * ((– 0,001) * ( – 0,33) +
+ (– 0,014) * ( – 0,08)) = 0,0002,
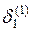 = 0,556 * (1 – 0,556) * ((– 0,001) * 0,27 + (– 0,014) * 0,79) = – 0,003.
= 0,556 * (1 – 0,556) * ((– 0,001) * 0,27 + (– 0,014) * 0,79) = – 0,003.
Вес первой связи выходного нейрона изменится, согласно (6.3), на следующую величину:
 = – 0,8
= – 0,8 
 = – 0,8 * (– 0,092) * 0,468 = 0,034.
= – 0,8 * (– 0,092) * 0,468 = 0,034.
Таким образом, новое значение веса будет равно:
 =
= 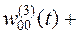
 = 0,062 + 0,034 = 0,096.
= 0,062 + 0,034 = 0,096.
Аналогично производится коррекция остальных весов связей ИНС:
 = 0,64 – 0,8 * (– 0,092) * 0,606 = 0,685;
= 0,64 – 0,8 * (– 0,092) * 0,606 = 0,685;
 = 0,04 – 0,8 * (– 0,092) * 1 = 0,114;
= 0,04 – 0,8 * (– 0,092) * 1 = 0,114;
 = -0,33 – 0,8 * (– 0,001) * 0,591 = – 0,329;
= -0,33 – 0,8 * (– 0,001) * 0,591 = – 0,329;
 = 0,27 – 0,8 * (– 0,001) * 0,556 = 0,27;
= 0,27 – 0,8 * (– 0,001) * 0,556 = 0,27;
 = – 0,084 – 0,8 * (– 0,001) * 1 = – 0,083;
= – 0,084 – 0,8 * (– 0,001) * 1 = – 0,083;
 = – 0,08 – 0,8 * (– 0,001) * 0,591 = – 0,073;
= – 0,08 – 0,8 * (– 0,001) * 0,591 = – 0,073;
 = 0,79 – 0,8 * (– 0,014) * 0,556 = 0,796;
= 0,79 – 0,8 * (– 0,014) * 0,556 = 0,796;
 = 0,037 – 0,8 (– 0,014) * 1 = 0,048;
= 0,037 – 0,8 (– 0,014) * 1 = 0,048;
 = 0,12 – 0,8 * 0,0002 * 0 = 0,12;
= 0,12 – 0,8 * 0,0002 * 0 = 0,12;
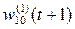 = 0,35 – 0,8 * 0,0002 * 1 = 0,35;
= 0,35 – 0,8 * 0,0002 * 1 = 0,35;
 = 0,02 – 0,8 * 0,0002 * 1 = 0,02;
= 0,02 – 0,8 * 0,0002 * 1 = 0,02;
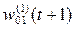 = – 0,5 – 0,8 * (– 0,003) * 0 = – 0,5;
= – 0,5 – 0,8 * (– 0,003) * 0 = – 0,5;
 = 0,24 – 0,8 * (– 0,003) * 1 = 0,242;
= 0,24 – 0,8 * (– 0,003) * 1 = 0,242;
 = – 0,015 – 0,8 * (– 0,003) * 1 = – 0,013.
= – 0,015 – 0,8 * (– 0,003) * 1 = – 0,013.
В случаях, когда вместо индекса начального нейрона связи стоит символ «–», производится настройка смещения нейрона. Т.е. запись  означает новое значение смещения у нейрона с индексом 1 во втором скрытом слое. Использованные для расчета значения ошибок выходов нейронов показаны на рис. 6.14.
означает новое значение смещения у нейрона с индексом 1 во втором скрытом слое. Использованные для расчета значения ошибок выходов нейронов показаны на рис. 6.14.

Рис. 6.14. Обратный проход для вычисления ошибок нейронов
Значения выходных сигналов ИНС при повторном подсчете выходов нейронов сети при использованном для коррекции весов наборе обучающих данных представлены в табл. 6.5 и на рис. 6.15.
Табл. 6.5. Значения выходных сигналов
нейронов после корректировки весов связей ИНС
| Номер слоя | Индекс нейрона | Значение выхода |
| 0,591 | ||
| 0,557 | ||
| 0,468 | ||
| 0,610 | ||
| 0,640 |
Новое значение ошибки ИНС для 2-го набора обучающих данных равно:
Е2 = 0,5 (1 – 0,641)2 = 0,065.
Напомним, что значение ошибки E2 до коррекции весов равнялось 0,075. Таким образом, в результате одного шага обучения значение ошибки уменьшилось на 0,01.
Для дальнейшего обучения ИНС на вход подается следующий вектор данных из обучающего множества и производится коррекция весов связей с учетом расхождения выходного сигнала ИНС и вектора требуемых выходных сигналов, соответствующего входному. Обучение ИНС продолжается до тех пор, пока ошибка выхода ИНС, вычисленная для всех наборов данных из обучающей выборки, по значению не будет меньше требуемой.
Дата добавления: 2014-12-23; просмотров: 512; Мы поможем в написании вашей работы!; Нарушение авторских прав |