Работа нейронной сети

Для того чтобы понять возможности применения ИНС, необходимо более подробно изучить особенности функционирования отдельных нейронов и ИНС в целом.

Для начала рассмотрим один простейший нейрон с двумя входами и пороговой функцией активации (рис. 6.7) с порогом q = 0. Тогда выход нейрона y равен 1, если взвешенная сумма входных сигналов больше либо равна 0. В обратном случае выходной сигнал нейрона равен 0.

Рис. 6.7. Нейрон с двумя входами и пороговой функцией активации

Области на плоскости входных сигналов, в которых значение выхода нейрона постоянно, показаны на рис. 6.8.

Рис. 6.8. Области с постоянным значением выходного сигнала для нейрона на рис. 6.7

Очевидно, что прямая, разделяющая эти области, имеет уравнение

.

Изменение весов связей нейрона приведет к изменению наклона прямой относительно координатных осей, а добавление в уравнение постоянного смещения вертикально смещает рассматриваемую прямую относительно оси Ox₁. При этом уравнение разделяющей прямой примет вид:

,

Настройкой значений весов связей и смещения можно добиться требуемого положения разделяющей прямой, например, для реализации с помощью ИНС логической операции «ИЛИ» (рис. 6.9).

Рис. 6.9. Пример разделяющей поверхности для нейрона, реализующего логическую операцию «ИЛИ»

Естественно, нейрон может иметь больше двух входных сигналов и отличную от пороговой функцию активации. Однако в этом случае в силу многомерности пространства входных сигналов значительно усложняется только визуальное представление зависимости выходного сигнала нейрона от входного вектора. Принцип работы формального нейрона остается неизменным: существуют области пространства входных признаков, в которых выходной сигнал нейрона принимает определенное значение. При этом разделяющая прямая также становится многомерной (ее размерность равна (n-1), где n – размерность вектора входных сигналов нейрона) и называется разделяющей гиперплоскостью.

Несколько нейронов, имеющие одинаковые входные сигналы, могут быть настроены (обучены) таким образом, чтобы реализовывать различные операции. Например, в случае использования двух нейронов с пороговой функции активации, один из нейронов может реализовать логическую операцию «ИЛИ», а другой – инверсию «И». Разделяющие гиперплоскости таких нейронов для двумерного входного вектора показаны на рис. 6.10.

Тогда, в случае, если выходные сигналы этих нейронов будут поданы на вход нейрона, обученного логической операции «И», то такая нейронная сеть из трех нейронов будет реализовывать логическую операцию «Исключающее ИЛИ», которую невозможно получить с использованием одного нейрона, т.к. невозможно провести единственного разделяющую гиперплоскость (прямую, для случая двух входных сигналов) таким образом, чтобы отделить пару сигналов (0; 1) и (1; 0) от пары сигналов (0; 0) и (1; 1).

Рис. 6.10. Примеры разделяющих поверхностей для нейронов, реализующих логические операции «ИЛИ» (нейрон 1) и инверсия «И» (нейрон 2)

Таким образом, правильная (с точки зрения рассматриваемой задачи) настройка разделяющих гиперплоскостей, соответствующих нейронам, позволяет реализовать с помощью сети связанных нейронов достаточно сложные функции и зависимости, что актуально при решении практических задач. При этом каскадная (многослойная) организация структуры связей нейронов дает возможность выделять в пространстве входных сигналов области достаточно сложной формы (в том числе и невыпуклые, и многосвязные), причем, чем больше используется слоев, тем более сложной может быть форма подобласти (рис. 6.11). Так для ИНС с нейронами с пороговой функцией активации без скрытых слоев возможно лишь линейное разделение пространства входных сигналов; с одним скрытым слоем – выделение односвязных выпуклых областей; с двумя и более скрытыми слоями – выделение областей произвольной формы и связности.

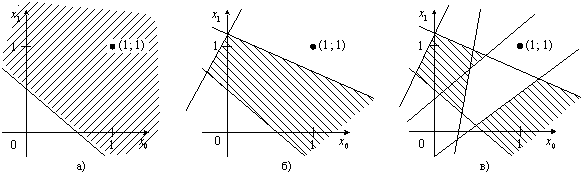
Рис. 6.11. Примеры зависимости формы выделяемых областей в пространстве входных сигналов от количества скрытых слоев в ИНС прямого распространения: а) нет скрытых слоев; б) 1 скрытый слой; в) 2 скрытых слоя

Использование функций активации, отличной от пороговой, например, сигмоидной, не приводит к значительному изменению характера разделяющей гиперплоскости. В этом случае в пространстве входного сигнала появляются области, соответствующие «переходным» значения выхода нейрона между 0 и 1.

Таким образом, работа многослойной нейронной сети может быть представлена как глобальное взаимодействие распределенных нейронов, каждый из которых выполняет локальную задачу (активизируясь при определенных значениях входных сигналов). Обучение такой ИНС подразумевает решение задачи стохастической аппроксимации отображения входных сигналов ИНС в выходные часто без извлечения информации о характере и свойствах самого отображения.

Принципиально другой подход используется в ИНС с радиально-базисными функциями активации – РБФ-сети. Особенностью радиально-базисных функций является то, что они принимают ненулевые значения только в некоторой окрестности точки , называемой центром, где n-количество входных сигналов нейрона. Примером такой функции может являться многомерная функция Гаусса:

,

где – вектор входных сигналов нейрона, – длина вектора а, – ширина радиальной функции. На рис. 6.12 показан пример, иллюстрирующий отличия разделяющих поверхностей для нейронов с пороговой и радиальной функциями активации.

Рис. 6.12. Вид разделяющих поверхностей для нейронов с пороговой (а) и радиальной (б) функциями активации

Структура РБФ-сети включает один скрытый слой с радиальными функциями активации нейронов и выходной слой с единственным нейроном с линейной функцией активации. Зависимость выходных сигналов ИНС от входных представляется в виде разложения по отдельным базисным функциям (соответствующих активационным функциям нейронов), веса которых определяются как веса соответствующих связей выходного нейрона. Таким образом, обучение РБФ-сетей сводится к поиску таких векторов центров и значений ширины активационных функций РБФ-нейронов, при которых достигается аппроксимация зависимости выходных сигналов ИНС от входных с требуемой точностью.