Лавина электронов

Если в газе между двумя электродами, образующими одно­родное поле, появляется свободный электрон, то двигаясь к аноду при достаточной напряженности электрического поля он может ионизиро­вать атом или молекулу газа при столкновении (рис. 1.3, а). В результате этого появляется новый (еще один) электрон и положительный ион. Этот электрон вместе с начальным ионизируют новые атомы и молеку­лы, и число свободных электронов непрерывно нарастает. Этот процесс получил название лавины электронов.

Интенсивность размножения электронов в лавине характери­зуется коэффициентом ударной ионизации а, равным числу ионизации производимых электроном на пути в 1 см по направлению действия электрического поля. Другое название коэффициента ударной иониза­ции — первый коэффициент Таунсенда.

В процессе развития лавины одновременно с электронами об­разуются положительные ионы. Подвижность ионов значительно мень­ше, чем электронов, и за время развития лавины они практически не ус­певают переместиться в промежутке к катоду. Таким образом, после прохождения лавины электронов в газе остаются положительные, а в электроотрицательных газах и отрицательные ионы, которые искажают (уменьшают или увеличивают) внешнее электрическое поле в проме­жутке. На рис. 1.5 приведено распределение напряженности электриче­ского поля в промежутке при прохождении его лавиной электронов. Видно, что напряженность электрического поля на фронте лавины воз­растает, в средней части, где находятся остающиеся положительные ио­ны, уменьшается, а вблизи катода вновь незначительно увеличивается.

Рис. 1.5. Искажение электрического поля в промежутке, созда­ваемое лавиной: 1 — средняя напряженность без лавины; 2 —результирующая напряженностъ

Для описания лавинного процесса необходимо определить число электронов в лавине. Предположим, что из катода за счет внешне­го ионизатора вырывается n₀ электронов (например n₀ = 1). На расстоя­нии x от катода число электронов возросло до n (рис. 1.6). Увеличение числа электронов dn на пути dx будет равно:

dn = n dx, (1.11)

или

. (1.12)

Интегрируя (1.12) по n от 1 до n и по x от 0 до x, получим:

. (1.13)

Рис. 1.6. Схема определения числа электронов в лавине

В однородном поле, где коэффициент ударной ионизации 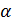= const, т. к. напряженность в любой точке промежутка одинакова, будем иметь:

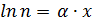, (1.14)

или

. (1.14а)

Выражение (1.14) дает значение электронов в лавине без учета их прилипания к нейтральным атомам и молекулам. Это явление харак­теризуется коэффициентом прилипания 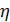. Коэффициент прилипания зависит от рода газа (электроотрицательный или электроположитель­ный). Тогда число электронов в лавине с учетом прилипания будет рав­но:

. (1.15)

Если n₀ больше 1, тогда (1.15) будет иметь вид:

. (1.16)

Число электронов в лавине n > 10⁷ .