
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 2. Дифракция света. Дифракция Френеля
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д.
Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта.

|
Согласнопринципу Гюйгенса – Френеля световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить, например, бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Если в качестве такой замкнутой поверхности выбрать одну из волновых поверхностей (волновой поверхностью называется геометрическое место точек, колебания в которых происходят в одинаковой фазе), то все бесконечно малые элементы этой замкнутой поверхности, как фиктивные источники, действуют синфазно. Это свойство фиктивных источников когерентных вторичных волн использовано в методе зон Френеля при изучении дифракции сферических волн точечного источника света.
Метод зон Френеля.Найдем в произвольной точке М амплитуду световой волны, распространяющейся от точечного источника света S (рис. 2).
|

Френель разбил волновую поверхность Ф, являющуюся сферической поверхностью с центром в точке S, на кольцевые зоны (зоны Френеля) такого размера, чтобы расстояния от краев соседних зон до точки М отличались на l/2 (рис. 2). Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположных фазах и при наложении взаимно ослабляют друг друга. Поэтому амплитуда А результирующего колебания в точке М определяется следующим образом:

где А1, А2, ..., Аn – амплитуды колебаний, возбуждаемых 1-ой, 2-ой, ..., n-ной зонами Френеля.
С ростом номера зоны Френеля интенсивность излучения в направлении точки М уменьшается, то есть  .
.
Амплитуда А результирующего колебания может быть представлена в виде:

так как выражения, стоящие в скобках, близки к нулю, а амплитуда An последней n-ной зоны Френеля ничтожно мала.
Таким образом, амплитуда результирующего колебания в произвольной точке М соответствует действию только половины центральной зоны Френеля.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого использованы зонные пластинки –в простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля, то есть прозрачных для нечетных зон, начиная с центральной зоны Френеля, и непрозрачных для четных зон Френеля. В этом случае результирующая амплитуда А (A=A1+A3+A5+...) должна быть больше, чем при полностью открытом волновом фронте. Опыт подтверждает эти выводы: зонные пластинки увеличивают освещенность в точке М , действуя подобно собирающей линзе.
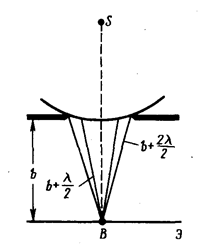 Дифракция Френеля на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием (рис. 3). Дифракционная картина на экране Э зависит от числа зон Френеля, открытых круглым отверстием. После разбиения открытой части волновой поверхности Ф на зоны Френеля, необходимо определить их
Дифракция Френеля на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием (рис. 3). Дифракционная картина на экране Э зависит от числа зон Френеля, открытых круглым отверстием. После разбиения открытой части волновой поверхности Ф на зоны Френеля, необходимо определить их
Рис. 3 число. Если для точки В, лежащей на линии, соединяющей источник S с центром отверстия (рис. 3), число открытых зон Френеля окажется четным, то в этой точке В будет наблюдаться темное пятно, так как колебания от каждой пары соседних зон Френеля взаимно гасят друг друга. Если же число открытых зон Френеля окажется нечетным, то в точке В будет наблюдаться светлое пятно. Причем для нечетного числа открытых зон Френеля амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны.
 Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.4). Пусть для точки В, лежащей на линии, соединяющей источник S с центром диска, после разбиения волновой поверхности Ф на зоны Френеля окажутся закрытыми диском m первых зон Френеля. Тогда амплитуда
Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.4). Пусть для точки В, лежащей на линии, соединяющей источник S с центром диска, после разбиения волновой поверхности Ф на зоны Френеля окажутся закрытыми диском m первых зон Френеля. Тогда амплитуда
Рис. 4 результирующего колебания в точке В равна:

 так как выражения, стоящие в скобках, обращаются в нули, а оставшаяся часть от амплитуды последней n-ной зоны ничтожно мала.
так как выражения, стоящие в скобках, обращаются в нули, а оставшаяся часть от амплитуды последней n-ной зоны ничтожно мала.
Следовательно, в точке В будет наблюдаться светлое пятно, соответствующее действию половины первой открытой зоны Френеля.
Дата добавления: 2014-12-23; просмотров: 408; Мы поможем в написании вашей работы!; Нарушение авторских прав |