АНАЛІЗ НЕПЕРЕРВНОЇ ЛІНІЙНОЇ САК

1.1. Для заданої функціональної схеми згідно варіанту та диференційних рівнянь їх окремих елементів одержати передатні функції цих елементівза відомими правилами перетворення Лапласа.Приклади таких перетворень наведені в пункті 1 додатку 1
(вирази 1-5).

1.2. На основі отриманих передатних функцій елементів скласти структурну схему системи (рис. 1.1.)

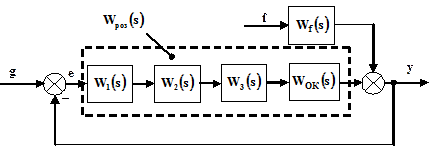
Рис. 1.1.

g – вхідний сигнал; y – вихідних сигнал; e – сигнал похибки;
f – сигнал збурення.

1.3. Визначити передатні функції розімкненої та замкненої САК за вхідною дією G(s):

; . (1.1)

Для визначення передатної функції на похибкою від G(s)перетворимо структурну схему рис. 1.1 до вигляду, зображеному на рис.1.2.

Рис. 1.2.

Тоді

. (1.2)

Для визначення передатної функції замкненої САК за збуренням 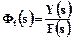, перетворимо структурну схему рис. 1.1. до вигляду, зображеному на рис. 1.3.

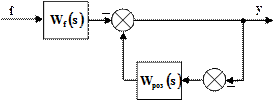
Рис. 1.3.

Тоді одержимо

, (1.3)

Аналогічні перетворення для конкретного прикладу наведені у виразах 1–13 додатку 1.

1.4. Визначити стійкість замкненої САК. Для цього використаємо характеристичне рівняння замкненої САК (1.3) А(s)=0, до якого можна застосувати критерії стійкості Рауса, Гурвіца, Михайлова. У додатку 1 (вирази 14–15) наведено застосування критерію Гурвіца.

1.5. Визначити запаси стійкості заданої САК за варіантом. Для цього можна використати критерій Найквіста, або логарифмічні частотні характеристики.

В пункті 6 додатку 1 наведено використання критерію Найквіста для конкретного прикладу з детальним поясненням кожного етапу розрахунку та одержаних результатів.

Фізичний зміст критерію Найквіста полягає в тому, що при збільшенні частоти вхідного впливу сигнал, що проходить по ланцюгу зворотного зв'язку, виявляється в протифазі з вхідним. А це рівнозначно заміні негативного зворотного зв'язку на позитивний. Якщо ж при цій частоті розімкнутий контур володіє підсиленням, то замкнута САУ стає нестійкою (будь-яке збільшення сигналу на виході призводить до збільшення сигналу на вході по ланцюгу зворотного зв'язку, що викликає подальше зростання вихідного сигналу тощо).

В пункті 7 додатку 1 для визначення запасів стійкості САК використані логарифмічні частотні характеристики розімкненої САК.

Основна ідея ґрунтується на наступному математичному правилі складання логарифмів. Якщо передатну функцію можна представити у вигляді дрібно-раціональної функції

, (1.4)

то:

. (1.5)

Після розбиття передатної функції на елементарні ланки можна побудувати ЛАФЧХ кожної окремої ланки, а результуючу ЛАФЧХ отримати простим додаванням.

При побудові ЛАЧХ для осі ординат звичайно використовується масштаб 20lg(X), тобто значення АЧХ, що дорівнює 100 перетворюється на 40 децибел шкали ЛАЧХ. Якщо передатна функція має вигляд:

, (1.6)

де – комплексна змінна, яку можна пов'язати з частотою, використовуючи наступну формальну заміну: 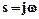, та – константи. Тоді побудувати ЛАЧХ можна використовуючи наступні правила:

в кожному , де (нуль), нахил лінії збільшується на дБ/декаду.

в кожному , де 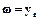(полюс), нахил лінії зменшується на дБ/декаду.

Початкове значення графіка можна знайти простий підстановкою значення кругової частоти в передатну функцію.

Початковий нахил графіка залежить від числа і порядку нулів і полюсів, які менше початкового значення частоти. Він може бути знайдений за допомогою перших двох правил.

1.6. Корекція динамічних характеристик САК. Якщо запаси стійкості заданої САК виявились меншими від загально прийнятих норм (на практиці, надійно працююча система повинна мати запас за амплітудою та за фазою ), або система виявилась нестійкою, то необхідно виконати корекцію динамічних характеристик.

Корекція системи відноситься до області синтезу систем, тому що при розрахунку корекції потрібно з'ясувати, які додаткові ланки повинні бути введені в систему для забезпечення заданих характеристик.

Зазвичай необхідні запаси стійкості і показники перехідного процесу забезпечуються за рахунок додавання відповідних коригувальних ланок послідовно з основними ланками або введення додаткових зворотних зв'язків.

У деяких випадках система без коригувальних ланок взагалі не може працювати, так як вона є структурно нестійкою, тобто має таку структуру, при якій годограф амплітудно-фазової характеристики при будь-якому підсиленні в контурі регулювання охоплює точку (-1, j0). Прикладом може служити система, яка містить дві інтегруючих ланки, з'єднаних послідовно.

Коригувальні пристрої використовуються також для зміни смуги пропускання системи, що дозволяє зменшити вплив перешкод. Коригувальні ланки мають особливо підібрані передавальні функції. Вони можуть включатися або послідовно з основними ланками САК, або паралельно їм.

Найбільше застосування отримали наступні послідовні коригувальні ланки: пропорційно-диференціюючі, пропорційно-інтегруючі, пропорційно-інтегро-діференціюючі.

Іншим видом коригувальних пристроїв є паралельні коригувальні пристрої, що реалізуються у вигляді місцевих зворотних зв'язків, що охоплюють одну або декілька ланок системи. Розрізняють два види зворотних зв'язків – жорсткий та гнучкий.

При жорсткому зворотному зв’язку, вихідна величина ланок, які охоплені цим зв'язком, подається на вхід. Жорсткий зворотній зв'язок впливає на систему як при перехідних процесах, так і в сталому стані.

При гнучкому зворотному зв’язку, на вхід передаються похідні вихідної величини цієї групи ланок. Гнучкий зворотній зв'язок впливає на систему тільки при перехідних процесах, тобто коли вихідний сигнал змінюється в часі.

В пунктах 8та9 додатку 1 наведено приклад використання послідовної корекції САК за допомогою пасивних корегуючих ланок. Використовуючи логарифмічні частотні характеристики розімкнутої САК, визначена структура та параметри корегуючої ланки. Послідовна корегуючи ланка включається в схему туди, де циркулюють слабкі за потужністю сигнали.

1.7. Побудувати перехідну характеристику скорегованої САК. Для цього на вхід замкненої САК необхідно подати ступеневий одиничний сигнал, тоді реакція САК на такий сигнал і буде перехідною характеристикою цієї системи. З рис. 1.1. видно, що . Тоді, якщо , то

. (1.7)

В пункті 10 додатку 1 наведено приклад побудови перехідного процесу типової САК. З графіку кривої перехідного процесу визначені якісні параметри скорегованої САК, такі як відносне перерегулювання та час перехідного процесу.

1.8. Визначити точність скорегованої САК при постійному , або при повільно змінному вхідному сигналі.

Похибка системи в такому режимі роботи визначається за формулою

(1.8)

де – коефіцієнти похибок. Останні визначаються з передатної функції скорегованої САК за похибкою

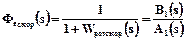(1.9)

за формулою

(1.10)

1.9. Визначити якість скорегованої системи за допомогою моделюванняв середовищі Simulink програмного пакету MATLAB. Для цього необхідно побудувати криву перехідного процесу при дії на її вході ступеневого сигналу та збурення згідно варіанту завдання.