Теорема Лиувилля.

Уравнение Лиувилля описывает эволюцию во времени плотности распределения систем ансамбля в фазовом пространстве.

Движение объемно-распределенного ансамбля в фазовом Г-пространстве аналогично ламинарному (без пе-ремешивания слоев) течению несжимаемой жидкости.

При этом и

Доказательство теоремы опирается

на то, что эволюция ρ определяется

уравнением неразрывности. Уравнение Лиувилля

Теорема Лиувилля При движении систем ансамбля в фазовом пространстве элементарные объемы остаются постоянными и могут меняться только по форме, сохраняя свою величину Теорема Лиувилля, т.е. постоянство фазового объема и сохранение плотности дает возможность упростить многие расчеты. Например, следствием теоремы является то, что число систем в фазовом объеме пропорционально величине объема, т.е.

11. Микроканоническое распределение Гиббса.

Микроканонический ансамбль Гиббса - статический ансамбль макроскопических систем, не обменивающихся энергией с окружающими телами при постоянном объёме и неизменном числе частиц. Адиабатический изолированная система.

Гиперповерхность энергий

измерений. Например, 3 - мерное пространство - 2 - мерная поверхность. Фазовая траектория изолированной системы лежит всеми точками на гиперповерхности энергий. Однако, правильнее рассматривать не системы, обладающие энергией Е = Е0, а системы, обладающие энергией в интервале от Е0 до Е0 + dE

При этом плотность распределения систем ансамбля внутри «энергетического гиперслоя» будет постоянна и не равна нулю, а вне этого слоя равна нулю.

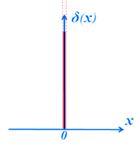
Дельта-функция Дирака

Дельта-функцию (функцию Дирака) вещественной переменной можно представлять себе как «функцию» δ(x), для которой выполняются следующие равенства:

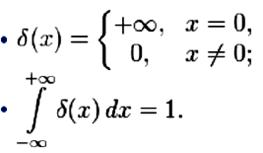
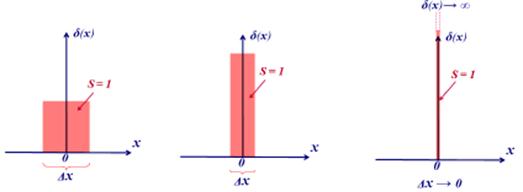В случае адиабатической изоляции все системы ансамбля (все фазовые точки) находятся в тонком энергетическом гиперслое с фазовым объемом Г0

При этом вероятность dω нахождения системы ансамбля в фазовом объеме dГ выражается при помощи дельта-функции Дирака

Можно показать, что из условия нормировки

следует Тогда вероятность dω нахождения системы ансамбля в фазовом объеме dГ

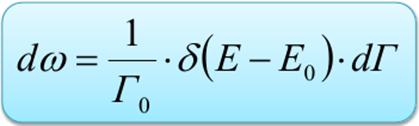
Микроканоническое распределение Гиббса а плотность вероятности χ

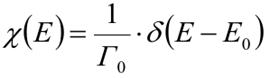Микроканоническое распределение показывает, что в изолированная система имеет только такие микросостояния, чтобы ее энергия была очень близкой к энергии Е0

12. Каноническое распределение Гиббса. Распределение Мак свелла.Канонический ансамбль Гиббса - статистический ансамбль макроскопических систем, находящийся в тепловом равновесии с термостатом при постоянном объеме и неизменном числе частиц.

Выделенная система легко обменивается энергией с окружающей средой при постоянной температуре, т.е. находится в термостате (изотермическая система). Разобьем каждую систему ансамбля на К подсистем, имеющих равное число молекул – N’.

Энергия системы

По теореме умножения вероятностей

Чтобы удовлетворить (1) и (2) необходимо, чтобы Тогда

- общий фазовый объем

Вероятность попадания системы в фазовый объем dГ Так как по условию нормировки вероятности то параметр а должен быть отрицательным, т.е. а < 0 В противном случае Удобно параметр а записать в

следующем виде:

Отрицательные абсолютные температуры (/4/, §94)

отрицательная абсолютная температура, величина, вводимая для описания неравновесных состоянийквантовой системы, в которых более высокие уровни энергии более населены, чем нижние. В равновесномсостоянии вероятность иметь энергию E_n определяется формулой:

. (1)

Здесь E_i — уровни энергии системы, k — Больцмана постоянная, Т — абсолютная температура,характеризующая среднюю энергию равновесной системы U = Σ(W_nE_n), Из (1) видно, что при Т > 0 нижниеуровни энергии более населены частицами, чем верхние. Если система под влиянием внешних воздействийпереходит в неравновесное состояние, характеризующееся большей населённостью верхних уровней посравнению с нижними, то формально можно воспользоваться формулой (1), положив в ней Т < 0. Однакопонятие О. т. применимо только к квантовым системам, обладающим конечным числом уровней, так как длясоздания О. т. для пары уровней необходимо затратить определённую энергию.

В термодинамике абсолютная температура Т определяется через обратную величину 1/Т, равнуюпроизводной энтропии (См. Энтропия) S по средней энергии системы при постоянстве остальныхпараметров х:

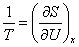
. (2)

Из (2) следует, что О. т. означает убывание энтропии с ростом средней энергии. Однако О. т. вводитсядля описания неравновесных состояний, к которым применение законов равновесной термодинамики носитусловный характер.

Пример системы с О. т.— система ядерных Спинов в кристалле, находящемся в магнитном поле, оченьслабо взаимодействующих с тепловыми колебаниями кристаллической решётки (См. Колебаниякристаллической решётки), то есть практически изолированной от теплового движения. Время установлениятеплового равновесия спинов с решёткой измеряется десятками минут. В течение этого времени системаядерных спинов может находиться в состоянии с О. т., в которое она перешла под внешним воздействием.

В более узком смысле О. т.— характеристика степени инверсии населённостей двух выбранныхуровней энергии квантовой системы. В случае термодинамического равновесия населённости N₁ и N₂уровней E₁ и E₂ (E₁ < E₂), т. е. средние числа частиц в этих состояниях связаны формулой Больцмана:

, (3)

где Т абсолютная температура вещества. Из (3) следует, что N₂ < N₁. Если нарушить равновесиесистемы, например воздействовать на систему монохроматическим электромагнитным излучением, частотакоторого близка к частоте перехода между уровнями: ω₂₁ = (E₂ — E₁)/ħ и отличается от частот другихпереходов, то можно получить состояние, при котором населённость верхнего уровня выше нижнего N₂ > N₁.Если условно применить формулу Больцмана к случаю такого неравновесного состояния, то по отношению кпаре энергетических уровней E₁ и E₂ можно ввести О. т. по формуле:

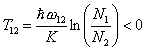
. (4)

Несмотря на формальный характер этого определения, оно оказывается в ряде случаев удобным,например позволяет описывать флуктуации в равновесных и неравновесных системах с О. т. аналогичнымиформулами.

Особенности применения статистического метода к квантованным системам

2. Функции распределения для квантованных систем. Распределение Бозе – Эйнштейна.

Функции распределения для квантованных систем. Распределение Ферми – Дирака.

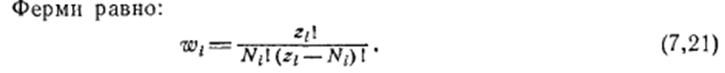
Феноменологическая термодинамика и статистическая физика.

Объекты и методы исследования.

Термодинамика и и статистическая физика являются частью теоретической физики и изучают общие свойства макроскопических физических систем (т.е. сист, состоящих из огромного числа микрочастиц: атомов, молекул, ионов, электронов и т.д.), находящихся в состоянии равновесия, а также общие закономер процессов установления равновесия.

Феноменологическая термодинамика не опирается ни на какие мо дельные представления об атомно-молекулярной структуре физических систем и механизмах молекулярных процессов в них. Это означает, что задачей термодинамики является установление связей между макроскпическими величинами, такими как давление, плотность, объем, температура, концентрации и т.д. Большинство этих величин пришло в темодинамику из других областей макроскопической физики. Характерне

отличие термодинамики от других макроскопических разделов физики

состоит в том, что в ней для полного макроскопического описания состояния равновесной системы вводятся дополнительные чисто термодинамические переменные: температура и энтропия. Термодинамика исходит из ряда установленных на опыте положений (называемых ее началами) и пользуется известными данными о свойствах тел.

Феноменологическая термодинамика, не будучи связана с модельны- ми представлениями, обладает весьма большой общностью и простотой, делающих ее мощным инструментом для решения многих технических задач (техническая термодинамика, теплотехника).

Если термодинамика исходит из известных свойств физических тел,3 то задача статистической физики заключается в объяснении или пред- сказании этих свойств, используя представления об атомно-молекулярной структуре физических систем и свойствах отдельных атомов, молекул или других микрочастиц, из которых состоит физическое тело. Таким образом, статистическая физика или статистическая механика представ- ляет собой атомно-молекулярную теорию макроскопических систем, т.е. микроскопическую теорию макроскопических тел.

На первый взгляд может показаться, что статистическая механика

должна быть просто механической теорией, применимой к системе из большого числа частиц. Составляя уравнение движения системы в числе, равном числу степеней свободы, и интегрируя их, мы, казалось бы, могли получить исчерпывающую информацию о движении системы. Однако, число этих уравнений будет v 1023 для одного моля. Решить эти уравнения практически невозможно. Однако, даже если бы мы смогли найти общее решение таких уравнений, то затем было бы необходимо выбрать те из них, которые соответствуют конкретным начальным и граничным условиям. Гранич условия опред-ся макроскопиче- скими внешними телами, которые в свою очередь состт из огромного числа частиц, наход в непрерывном тепловом движении. Таким образом, получение решения такой системы становится принципиально невозможным. С другой стороны, казалось бы, увеличение числа частиц должно привести к невообразимой сложности и запутанности свойств систем, состоящих из большого числа частиц, и что в поведении макроскопиче- ского тела мы не сможем найти и следов какой-либо закономерности.

При большом числе частиц, составляющих рассматриваемую систему, появляются новые своеобразные закономерности – так называемые статистические закономерности, – обусловленные именно наличием большого числа частиц в системе. Таким образом, хотя движение системы, состоящей из большого числа частиц, подчиняется тем же законам механики, что и системы из небольшого числа частиц, наличие большого числа частиц приводит к качественно новым закономерностям.

Значение статистической физики в ряду других разделов теоретической физики определяется тем, что в природе мы постоянно встречаемся с макроскопическими телами, поведение которых в силу указанных причин не может быть исчерпывающе описано чисто механическими ме тодами и которые подчиняются статистическим закономерностям.

В завис от того, по каким законам движутся частицы, разли чают классическую и квантовую статистическую физику. Кроме того, статистическую физику делят на две части: собственно статистиче скую физику и физическую кинетику. В собственно статистической фи зике ограничив рассмотр свойств макроскопич систем, состояние которых не изменяется во времени. Сост макроскопической системы, в которых она может находиться неопределенно долгое время называют равновесным.

Общие закон-ти сравнительно мало зави сят от конкретных свойств атомов и молекул, из которых сост система и которые мы дальше будем называть микрочаст, имея в виду, чт могут рассм-ся системы не только их атомов и молекул, но из нейтронов, электронов и других частиц.

В стат физике удается установить общие законы поведе ния всех макр систем, находящихся в равновесии. В частности, универсальные законы теплового поведения макроскопических тел (законы термодинамики). Таким образом, предмет статистической физики гораздо шире, чем термодинамики, т.к. законы термодинамики мы здесь получаем как частный случай, когда рассматриваем тепловое по ведение системы.

Изучением свойств макроскопических систем, не находящихся в рав новесии, занимается физическая кинетика. Ясно, что законы изменения состояния макроскопических систем – законы физической кинетики являются гораздо более сложными, чем законы, определяющие повед ние равновесных систем. В физической кинетике практически не удалось выявить конкретные законы изменения состояния во времени, имеющие универсальный характер. В настоящее время найдены только законы поведения неравновесных систем, имеющих простейший характер.

Стат физика, как наука о свойствах физических тел, сстоящих из огромного числа отдельных частиц, ведет свое начало от М. В. Ломоносова, выдвинувшего еще в середине XV III века концепцию, согласно которой тепловые явления объясняются хаотическим движени- ем этих частиц. Во второй половине XIX века эти же представления послужили основой, на которой была развита кинетическая теория материи Д.К.Максвеллом и Л.Больцманом, давшим статистическое обоснование термодинамики. Наконец, наиболее последовательная и полная форма статистической механики, применимая к любым макроскопическим телам была дана в 1901 году Д.У.Гиббсом. В основе математического аппарата статистической физики лежит теория вероятности. Термодинамика — это наука о закономерностях превращения энергии.

Название ее происходит от гр. слов „термос“— тепло и „динамос“— сила. Основы термодин были заложены в XIX веке, когда, в связи с развитием тепловых двигателей, возникла необход изучения закономерностей превращения тепловой энергии в работу. Современная термодин яв-ся основой теории тепловых двигателей, тепловых машин, различ устройств и технологич процессов, в которых в качестве исход энергии, претерпевающей изменение в рабочем процессе, применяется тепловая энергия, т.е. научной базой совр энергетики. Значение термодинамики заключается в том, что она устанавливает принципы наиболее эффективного или оптимального преобразования разл видов энергии.

В отличие от многих др. наук, термодин не оперирует какимилибо модельными представлениями строения вещества и вообще непосредственно не связана с представлением о микроструктуре вещества.Поэтому к понятию о молекулярном строении вещества мы будем прибегать только для облегчения понимания отдельных понятий термодинамики.

В основу термодинамики положен ряд законов (или, как иначе говорят, начал), установленных опытным путем, с которыми мы познакомимся чуть позже, рассмотрев предварительно некоторые термодинамические понятия

Внешние и внутренние термодинамические параметры. Давление.

Существуют три основных состояния вещества: твердое, жидкое, газообразное. Очевидно, что одно и то же вещество при разных условиях может находиться в различных состояниях. Для определения конкретных физических условий, при которых рассматривается вещество, вводят удобные характеристики состояния вещества, так называемые, параметры состояния системы. Параметры делятся на: внешние внутренние определяются расположением тел, окружающих систему, и характеризуют как бы силовые воздействия на систему (объем, напряженности различных силовых полей,...) определяются совокупным движением частиц системы, их взаимным расположением (плотность, энергия, поляризуемость, намагниченность,...)

Приведем примеры внутренних и внешних параметров. Пусть газ заклюен в сосуде с твердыми стенками. Объем сосуда определяется положением внешних тел – стенок. Это внешний параметр. Давление, оказываемое газом на стенку сосуда, зависит от скоростей теплового движения его молекул. Оно является внутренним параметром.

Допустим теперь, что газ заключен в цилиндре под поршнем, который может свободно перемещаться. Пусть на поршне лежит груз веса M. Если площадь поршня равна S, то груз M оказывает давление Р = Mg/S на каждую единицу площади поршня. Давление Р в таком смысле будет внешним параметром, так как оно определяется весом внешнего тела - груза M. Объем газа V определяется положением подвижной стенки сосуда - поршня. Однако теперь объем V становится внутренним параметром, так как положение поршня с грузом зависит от внутреннего давления, оказываемого газом на поршень.

Если газ двух- или многоатомный, то при его нагревании молекулы диссоциируют, т.е. распадаются на атомы или группы атомов. При далнейшем нагревании атомы газа ионизуются - расщепляются на заряжен-

ные ионы или электроны. Отношение числа диссоциировавшихся моле-кул к общему числу их называется степенью диссоциации молекул газа.

Аналогично определяется степень ионизации его, как отношение числа ионизовавшихся атомов к общему числу их. Степень диссоциации и степень ионизации газа - внутренние параметры. В электрическом поле газ поляризуется, а в магнитном – намагничивается, возникают электрический и магнитный моменты газа. Эти величины являются внутренними параметрами. Напряженности же внешних электрического и магнитного полей, в которых помещен газ, являются параметрами внешними.

Термодинамические параметры разделяются также на:7

интенсивные экстенсивные не зависят от числа частиц системы и характеризуют общее состояние теплового движении тела зависят от числа частиц; при одних и тех же значениях интенсивных параметров пропорциональны общей массе или количеству частиц тела

Наиболее распространенными интенсивными параметрами состояния вещества являются: абсолютное давление, удельный объем, абсолютная температура.

Абсолютное давление — величина, характеризующая интенсивность нормальных (перпендикулярных) к поверхности сил F, с которыми тело действует на единицу площади поверхности S. Если распределение сил по поверхности тела равномерно (как бывает в жидкостях и газах), то давление Р = F/S. Различают абсолютное и избыточное давления.

Абсолютное давление - это полное давление, производимое газом или паром. Избыточное давление представляет собой разность абсолютного и барометрического давлений (барометрическое давление - это давление атмосферы). Параметром состояния является только абсолютное давление, поскольку не зависит от состояния окружающей среды (давления окружающего воздуха). Давление измеряется в системе СИ в паскалях:

1Па = 1Н/м

. В технических расчетах часто пользуются другими единицами: баром (1бар = 105Па), кгс/см2, атмосферами техническими (ат) или физическими (атм), а также высотой ртутного или водяного столба.

Связь между указанными единицами измерения давления следующая:

1 МПа = 10 бар = 10, 2 ат = 10, 2 кгс/см2;

1 ат = 1, 0 кгс/см2 = 735, 6 мм рт.ст. = 10 м вод.ст. = 0, 981 бар = 0, 0981 МПа;

1 атм = 1, 0333 кгс/см2 = 10333 кгс/м

= 760 мм рт.ст. = 10, 333 м вод.ст.

Нулевое начало термодинамики. Определение температуры. Сравнение температуры

Адиабатически изолированные, термодинамически равновесные системы образуют при приведении их в тепловой контакт общую термодинамически равновесную систему только при условии равенства температур исходных систем.

Таким образом, термодинамическое состояние адиабатически изолированной равновесной системы, очевидно, определяется всеми внешними параметрами и внутренним параметром — температурой.

Следовательно, все равновесные внутренние параметры термодинамической системы являются функциями внешних параметров и температуры. Температура — это величина, характеризующая направление воз можного самопроизвольного перехода теплоты между телами. Теплот может самопроизвольно переходить лишь от тел с более высокой температурой к телам с более низкой температурой.

С молекулярной точки зрения, температура определяется как физческая величина, пропорциональная средней кинетической энергии движения молекул и атомов вещества. Для количественного задания температуры используют температурные шкалы. В промышленности России употребляется шкала Цельсия, в которой интервал от точки плавления льда, принятой за нуль, до точки кипения воды при нормальном (атмосферном) давлении разбит на 100 равных частей (градусов). Обозначение – ◦С.

В физике чаще используется понятие абсолютной температуры — температуры, отсчитываемой от абсолютного нуля. Абсолютный нульможет быть определен как такая температура, при которой в теле пре кращается тепловое движение частиц. В абсолютной шкале для температуры тройной точки воды принято значение 273,16. Интервал между абсолютным нулем и температурой тройной точки разделен на 273,16частей и каждая часть названа Кельвином (К). Температура по шкале

Кельвина обозначается Т:

T = t + 273, 15,

где t - температура в градусах Цельсия. (Тройная точка воды — это со-стояние, при котором находится в равновесии все три фазы воды: твердая (лед), жидкая (вода) н газообразная (пар). Температура таяния льда при нормальном давлении ниже температуры тройной точки на 0,01 ◦С.)

Термометр. Термометрические тело и величина, требования к ним. Температурные шкалы. Абсолютный нуль

Термо́метр (греч. θέρμη — тепло; μετρέω — измеряю) — прибор для измерения температуры воздуха, почвы, воды и так далее. Существует несколько видов термометров

Термометрическое тело – это тело, для которого известна зависимость какого-либо свойства данного тела от температуры. Термометрическим телом может быть, например, жидкость или газ, для которого известна зависимость изменения его объёма от температуры.

Эмпирическая шкала – это температурная шкала, установленная с помощью термометрического тела.

Наиболее распространён способ измерения температуры с помощьюжидкостного термометра, в котором используется расширение жидкости (изменение объёма) при нагревании.

При градуировке термометра отмечают опорные точки, расстояние между которыми на шкале делят на равные части, кот называ градусами.