Уравнение Клапейрона-Клаузиуса.

Уравнение Клапейрона — Клаузиуса — термодинамическое уравнение, относящееся к квазистатическим (равновесным) процессам перехода вещества из одной фазы в другую (испарение, плавление, сублимация, и др.).

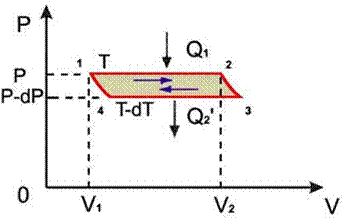
Предположим, что при подводе к одной из фаз двухфазной среды некоторого количества теплоты Q₁, происходит переход части вещества, массой M, из первой фазы во вторую. Так как рассматриваемый переход считается квазиравновесным, то давление и температура при его осуществлении постоянны: P = const и T =const.

Удельный объем, определяемый как отношение объема фазы к ее массе для первой фазы равен n₁, а второе соответственно n₂. Количество вещества массой М занимает в первой фазе объем V₁= n₁M, а во второй объем V₂= n₂M.

Переход вещества из первой фазы во вторую изображен на рисунке как участок 1-2 некоторого кругового процесса, с помощью которого количество вещества массой М возвращается в исходное состояние в первой фазе. Будем считать, что этот круговой представляет собой цикл Карно. Тогда процессы 2-3 и 4-1 являются адиабатическими, а изотермический процесс 3-4 описывает теплоотдачу при переходе вещества из второй фазы в первую. Считаем, что процесс 3-4 осуществляется при давлении P - dP и температуре T - dT, значения которых бесконечно близки к значениям давления P и температуры Т протекания процесса 1-2.

На основании первой теоремы Карно можно записать выражение для к.п.д. рассматриваемого цикла

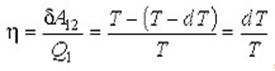
Где dА₁₂ совершаемая за цикл работа. С учетом бесконечной малости величины dP в полном приближении можно считать, что работа dА₁₂ совершаемая за цикл Карно близка к работе цикла, представляющего собой прямоугольник бесконечно малой высоты. Это позволяет заменить адиабаты на боковых сторонах цикла Карно вертикальными отрезками при V = const, т.е. представить цикл Карно в виде прямоугольника, высота которого равна бесконечно малой величине dP. В этом приближении имеем

Фазовые переходы первого рода количественно характеризуются величиной удельной теплоты фазового перехода, которая численно равна количеству теплоты сообщаемой единице массы вещества для осуществления фазового перехода:

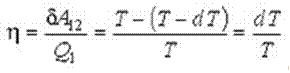
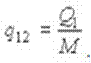
Тогда, с учетом представленных формул, можно записать

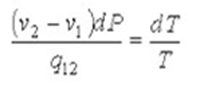
Уравнение Клапейрона-Клаузиуса: