Интегрирование по частям

Способ основан на известной формуле производной произведения:

(uv)¢ = u¢v + v¢u

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

или ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Интегрирование элементарных дробей

Определение: Элементарныминазываются дроби следующих четырех типов:

I. III.

II. IV.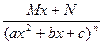

m, n – натуральные числа (m ³ 2, n ³ 2) и b² – 4ac <0.

Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

I.

II.

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Пример.

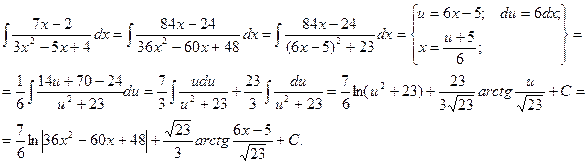
Вообще говоря, если у трехчлена ax² + bx + c выражение b² – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.

Пример.

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.

Сначала рассмотрим частный случай при М = 0, N = 1.

Тогда интеграл вида можно путем выделения в знаменателе полного квадрата представить в виде . Сделаем следующее преобразование:

.

Второй интеграл, входящий в это равенство, будем брать по частям.

Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл .

Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u² + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Пример: