Связь градиента с производной по направлению

Теорема: Пусть задана функция u = u(x, y, z) и поле градиентов

.

Тогда производная 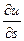по направлению некоторого вектора 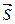равняется проекции вектора gradu на вектор .

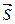Доказательство: Рассмотрим единичный вектор 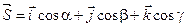и некоторую функцию u = u(x, y, z) и найдем скалярное произведение векторов 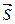и gradu.

Выражение, стоящее в правой части этого равенства является производной функции u по направлению s.

Т.е. . Если угол между векторами gradu и 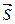обозначить через j, то скалярное произведение можно записать в виде произведения модулей этих векторов на косинус угла между ними. С учетом того, что вектор 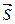единичный, т.е. его модуль равен единице, можно записать:

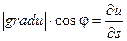
Выражение, стоящее в правой части этого равенства, и является проекцией вектора gradu на вектор .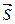

Для иллюстрации геометрического и физического смысла градиента скажем, что градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой- либо точке. В физике существуют такие понятия как градиент температуры, градиент давления и т.п. Т.е. направление градиента есть направление наиболее быстрого роста функции. С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.