Производная по направлению

Рассмотрим функцию u(x, y, z) в точке М( x, y, z) и точке М₁( x + Dx, y + Dy, z + Dz).

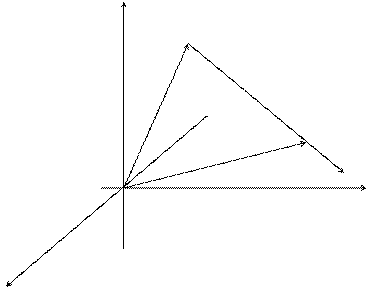
Проведем через точки М и М₁ вектор 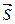. Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусамивектора .

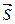Расстояние между точками М и М₁ на векторе 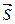обозначим DS.

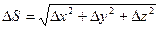
Высказанные выше предположения, проиллюстрируем на рисунке:

z

M

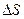
M₁

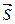
Далее предположим, что функция u(x, y, z) непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:

,

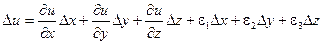где величины e₁, e₂, e₃ – бесконечно малые при .

Из геометрических соображений очевидно:

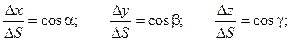
Таким образом, приведенные выше равенства могут быть представлены следующим образом:

;

Заметим, что величина s является скалярной. Она лишь определяет направление вектора .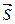

Из этого уравнения следует следующее определение:

Определение: Предел 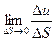называется производной функции u(x, y, z) по направлению вектора 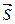в точке с координатами ( x, y, z).

Пример. Вычислить производную функции z = x² + y²x в точке А(1, 2) по направлению вектора . В (3, 0).

Решение. Прежде всего необходимо определить координаты вектора .

=(3-1; 0-2) = (2; -2) = 2 .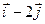

Далее определяем модуль этого вектора:

=

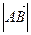Находим частные производные функции z в общем виде:

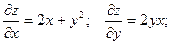
Значения этих величин в точке А :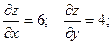

Для нахождения направляющих косинусов вектора производим следующие преобразования:

=

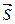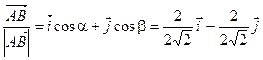
За величину 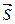принимается произвольный вектор, направленный вдоль заданного вектора, т.е. определяющего направление дифференцирования.

Отсюда получаем значения направляющих косинусов вектора :

cosa = 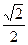; cosb = -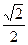

Окончательно получаем: 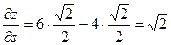- значение производной заданной функции по направлению вектора .